פונקציה



בערך זה |
במתמטיקה, פוּנְקְצִיָּה (נקראת גם העתקה) היא התאמה, המשייכת לכל איבר בקבוצה אחת, איבר יחיד בקבוצה שנייה. זהו מושג כללי ביותר, המופיע בכל תחומי המתמטיקה, וגם מחוץ לה. הפונקציה משמשת בין השאר ככלי לבטא תלות בין משתנים (מצב בו שני משתנים תלויים זה בזה) וככזו מאפשרת הצגה פורמלית של אופי התלות בין גדלים שונים בתחומי המדע, ההנדסה והכלכלה.
הגדרה פורמלית
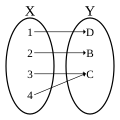
פונקציה מקבוצה $ X $ לקבוצה $ Y $ מסומנת $ f\colon X\to Y $ ובקיצור $ f $.
הקבוצה $ X $ קרויה תחום הפונקציה (או תחום ההגדרה של הפונקציה). זוהי קבוצת כל האיברים עליהם הפונקציה מוגדרת. הקבוצה $ Y $ קרויה טווח הפונקציה. זוהי קבוצת כל האיברים שהפונקציה יכולה להתאים לאיבר מ-$ X $. אומרים שהפונקציה "מקבלת" איברים מהתחום $ X $ ו"מחזירה" איברים מהטווח $ Y $.
מבחינה פורמלית פונקציה $ f $ היא תת-קבוצה של המכפלה הקרטזית $ X\times Y $ (כלומר קבוצה של זוגות סדורים שהאיבר הראשון בכל זוג הוא מ-$ X $ והשני מ-$ Y $) שמקיימת את שני התנאים הבאים:
- לכל $ x\in X $ קיים $ y\in Y $ כך ש-$ (x,y)\in f $ (סריאליות (אנ')).
- לכל $ x\in X $, $ y_{1},y_{2}\in Y $ אם $ (x,y_{1})\in f $ וגם $ (x,y_{2})\in f $ אז $ y_{1}=y_{2} $ (חד ערכיות).
קבוצת הזוגות הסדורים המרכיבה את $ f $ קרויה גרף הפונקציה. זאת משום שבמקרה הפרטי של פונקציות ממשיות ניתן לתאר אותה באופן ויזואלי כגרף במערכת צירים קרטזית.
מסמנים $ f(x)=y $ אם ורק אם $ (x,y)\in f $. במקרה כזה האיבר $ y $ קרוי התמונה של $ x $, ו-$ x $ קרוי מקור של $ y $ (אך לא המקור שכן ייתכנו כמה מקורות לאיבר מסוים. אם קיים לכל איבר מקור יחיד, נאמר שהפונקציה חד-חד-ערכית). התנאי הראשון מבטיח שלכל $ x $ ב-$ X $ יש תמונה. התנאי השני מבטיח שתמונה זו היא יחידה. יחס שהוא גם חד ערכי וגם מלא נקרא פונקציה.
אם מוותרים על התנאי הראשון (לא לכל איבר יש בהכרח תמונה) אז מתקבלת פונקציה חלקית, ואם מוותרים על התנאי השני (ייתכנו איברים עם יותר מתמונה אחת) מתקבלת פונקציה מרובה. אם מוותרים על שני התנאים יחדיו מתקבל יחס במובנו הכללי.

שתי פונקציות $ f,g $, עם אותו תחום וטווח (פורמלית אין צורך להניח כי יש להן את אותו טווח, רק אותו תחום), מוגדרות כשוות רק כאשר $ f(x)=g(x) $ לכל $ x\in X $.
לכל $ Z\subseteq X $ (תת-קבוצה כלשהי של $ X $) הקבוצה $ f(Z) $ (לפעמים מסומנת גם $ f[Z] $) היא תת-קבוצה של $ Y $ המוגדרת: $ f(Z)=\{f(z)\mid z\in Z\} $. כלומר זוהי התת-קבוצה של $ Y $ הכוללת את כל האיברים שהם תמונות של איברי $ Z $. אומרים על $ f(Z) $ שהיא התמונה של $ Z $. בפרט, הקבוצה $ f(X) $ הכוללת את כל האיברים ב-$ Y $ שהם תמונה של איבר כלשהו ב-$ X $, נקראת התמונה של הפונקציה $ f $ ומסומנת לעיתים $ \operatorname {Im} (f) $ או $ \operatorname {im} (f) $.
לכל $ Z\subseteq Y $ הקבוצה $ f^{-1}(Z) $ היא תת-קבוצה של $ X $ המוגדרת: $ \{x\in X\mid f(x)\in Z\} $. כלומר זוהי התת-קבוצה של $ X $ הכוללת את כל האיברים שהתמונה שלהם היא איבר ב-$ Z $. אומרים על $ f^{-1}(Z) $ שהיא המקור של $ Z $.
אם $ f\colon X\to Y $ היא פונקציה, ו-$ Z\subseteq X $, אז הפונקציה $ f|_{Z}\colon Z\to Y $ המוגדרת $ f|_{Z}(z)=f(z) $, נקראת הצמצום של $ f $ ל-$ Z $. זוהי הפונקציה שזהה לפונקציה $ f $, רק שתחומה הוא $ Z $.
תכונות של תמונות ומקורות
לכל איבר ב-$ X $ יש תמונה יחידה, אבל לאיבר ב-$ Y $ יכולים להיות כמה מקורות או אף מקור בכלל. לכן באופן כללי לא תמיד מתקיים $ f^{-1}(f(Z))=Z $ או $ f(f^{-1}(Z))=Z $. היחסים הבאים תמיד מתקיימים:
- לכל $ Z\subseteq Y $ מתקיים $ f(f^{-1}(Z))\subseteq Z $.
- לכל $ Z\subseteq X $ מתקיים $ Z\subseteq f^{-1}(f(Z)) $.
- $ f(f^{-1}(Z))=Z $ אם ורק אם $ Z\subseteq f(X) $.
- $ X=f^{-1}(Y)=f^{-1}(f(X)) $.
דוגמאות
- ההתאמה המתאימה לכל אדם את גילו היא פונקציה מקבוצת האנשים לקבוצת המספרים הטבעיים, כי לכל אדם יש גיל יחיד.
- ההתאמה המתאימה לכל מספר ממשי את ריבועו היא פונקציה מקבוצת המספרים הממשיים לעצמה. ניתן לתארה באמצעות השוויון $ f(x)=x^{2} $.
- ההתאמה המתאימה לכל אדם את המדינה שבה הוא אזרח אינה פונקציה מאחר שיש אנשים בעלי מספר אזרחויות.
- ההתאמה המתאימה לכל אדם את מד הכושר שלו בשחמט אינה פונקציה כי יש אנשים שאינם מדורגים על ידי פיד"ה.
תכונות של פונקציות
בתחומים שונים של המתמטיקה חוקרים ומתעניינים בתכונות שונות ומגוונות של פונקציות. על פי רוב מדובר בתכונות הקשורות במבנה המוגדר על התחום או הטווח של הפונקציה (למשל רציפות של פונקציות ממשיות ושימור מרחק של איזומטריות). עם זאת ישנן מספר תכונות כלליות של פונקציות שאינן תלויות כלל במבנה של הקבוצות עליהן הן מוגדרות.
- פונקציה $ \ f\colon X\to Y $ נקראת חד-חד ערכית (חח"ע) אם מתקיים: $ \ f(x_{1})=f(x_{2})\Rightarrow x_{1}=x_{2} $. כלומר אם לכל שני איברים שונים זה מזה בתחום מותאמים שני איברים שונים זה מזה בטווח. במילים אחרות, לכל איבר בטווח יש לכל היותר מקור אחד.
- פונקציה $ \ f\colon X\to Y $ נקראת על אם לכל $ y\in Y $ קיים $ x\in X $ כך ש-$ f(x)=y $. כלומר אם התמונה של הפונקציה שווה לטווח שלה ($ f(X)=Y $). במילים אחרות, לכל איבר בטווח יש לפחות מקור אחד. במקרה כזה גם אומרים ש-$ f $ היא פונקציה על $ Y $.
- פונקציה חד-חד-ערכית ועל (חחע"ע) היא פונקציה שהיא הן חד-חד-ערכית והן על. לפונקציה שכזו מתקיים שלכל איבר בטווח יש בדיוק מקור אחד. קיום פונקציה שכזו בין שתי קבוצות מראה שהן שקולות. שם אחר לפונקציה חחע"ע $ f\colon X\to Y $ הוא פונקציה הפיכה. זאת משום שלפונקציות שכאלו ניתן להגדיר פונקציה הופכית: $ f^{-1}\colon Y\to X $ המקיימת $ f^{-1}(y)=x $ לכל $ y\in Y $, כאשר $ x $ הוא האיבר היחיד ב-$ X $ המקיים $ f(x)=y $. אם $ f\colon X\to Y $ היא פונקציה הפיכה, אז לכל $ x\in X $ ולכל $ y\in Y $ מתקיים: $ f^{-1}(f(x))=x $ ו-$ f(f^{-1}(y))=y $.
- פונקציה $ f\colon X\to X $ (מקבוצה לעצמה) שהיא חד-חד-ערכית ועל נקראת תמורה.
- על איבר $ z\in X\cap Y $ (איבר שנמצא הן ב-$ X $ והן ב-$ Y $) נאמר שהוא נקודת שבת של $ f\colon X\to Y $ אם מתקיים $ f(z)=z $.
-
פונקציה חח"ע אך לא על -
פונקציה על אך לא חח"ע -
פונקציה חח"ע ועל (הפיכה) -
פונקציה לא חח"ע ולא על
מקרים בסיסיים
להלן דוגמאות לפונקציות בסיסיות המוגדרות באופן כללי לקבוצות ללא תלות במבנה מסוים.
פונקציית הזהות
 ערך מורחב – פונקציית הזהות
ערך מורחב – פונקציית הזהות
פונקציית הזהות על קבוצה $ X $ היא פונקציה $ I\colon X\to X $ המוגדרת $ I(x)=x $ לכל $ x\in X $. כאשר רוצים להדגיש שמדובר בפונקציית הזהות של קבוצה מסוימת $ X $ מסמנים את הפונקציה כ-$ I_{X} $. פונקציית הזהות היא פונקציה חד-חד-ערכית ועל (ולכן גם תמורה). כל איבר ב-$ X $ הוא נקודת שבת שלה. הפונקציה ההופכית שלה היא היא עצמה ($ f=f^{-1} $). פונקציית הזהות היא איבר היחידה ביחס להרכבת פונקציות (כמפורט בהמשך). היא משמשת כדי להראות שכל קבוצה שקולה לעצמה.
הפונקציה הריקה
 ערך מורחב – הפונקציה הריקה
ערך מורחב – הפונקציה הריקה
הפונקציה הריקה לקבוצה $ Y $ היא הפונקציה היחידה $ f\colon \emptyset \to Y $. כלומר זוהי הפונקציה היחידה מהקבוצה הריקה לקבוצה כלשהי $ Y $. מכיוון שבקבוצה הריקה אין איברים, הפונקציה לא מקבלת שום איבר ואין אף איבר ב-$ Y $ שיש לו מקור ביחס אליה. הפונקציה מקיימת את התנאים שבהגדרת הפונקציה באופן ריק. הפונקציה היא חד-חד-ערכית (באופן ריק), אך אינה על, למעט במקרה $ Y=\emptyset $.
פונקציה קבועה
 ערך מורחב – פונקציה קבועה
ערך מורחב – פונקציה קבועה


פונקציה $ f\colon X\to Y $ שמקיימת שלכל $ x_{1},x_{2}\in X $ מתקיים $ f(x_{1})=f(x_{2}) $ נקראת פונקציה קבועה. הפונקציה הריקה היא קבועה באופן ריק. אם $ f $ היא פונקציה קבועה שאינה הפונקציה הריקה, אז קיים $ y_{0}\in Y $ כך שלכל $ x\in X $ מתקיים $ f(x)=y_{0} $ (ואז מסמנים $ f(x)\equiv y_{0} $). אם $ X $ אינה ריקה ואינה יחידון, אז אף פונקציה קבועה ממנה אינה חד-חד-ערכית (לעומת זאת כל פונקציה מיחידון היא חד-חד-ערכית). אם $ Y $ אינה ריקה ואינה יחידון, אז פונקציה קבועה אליה אינה על.
פונקציה מציינת
 ערך מורחב – פונקציה מציינת
ערך מורחב – פונקציה מציינת
פונקציה $ 1_{Z}\colon X\to \{0,1\} $ נקראת פונקציה מציינת של תת-קבוצה $ Z\subseteq X $ אם לכל $ x\in X $ מתקיים:
- $ 1_{Z}(x)=\left\{{\begin{matrix}1&{\mbox{if}}\ x\in Z\\0&{\mbox{if}}\ x\notin Z\end{matrix}}\right. $
כלומר זאת פונקציה שמחזירה $ 1 $ לכל איבר של $ Z $, ומחזירה $ 0 $ לכל איבר שאינו ב-$ Z $.
הפונקציה המציינת מסומנת גם $ \chi _{Z} $.
פונקציה $ n $-מקומית
פונקציה $ n $-מקומית או פעולה $ n $-ארית היא פונקציה מהצורה $ f\colon X^{n}\to X $. כאשר $ X^{n}=\underbrace {X\times \cdots \times X} _{n{\text{ times}}} $ היא קבוצת ה-n-יות הסדורות של איברי $ X $. כאשר רושמים את התמונה של פונקציה $ n $-מקומית מקובל להשמיט את הסוגריים של ה-$ n $-יה הסדורה. כלומר רושמים $ f(x_{1},\ldots ,x_{n}) $ במקום $ f((x_{1},\ldots ,x_{n})) $.
פונקציה $ 1 $-מקומית נקראת גם פעולה אונארית. זוהי פשוט פונקציה $ f\colon X\to X $ רגילה.
המקרה החשוב ביותר הוא של פונקציה $ 2 $-מקומית, הקרויה גם פעולה בינארית. זוהי פעולה המתאימה לכל זוג סדור של איברים בקבוצה, איבר בקבוצה. הדוגמאות המוכרות ביותר לפעולות בינאריות הן ארבע פעולות החשבון המוגדרות על קבוצות של מספרים. במקרה כזה נהוג להחליף את הסימון הסטנדרטי לתמונת הפונקציה בסימן פעולה שמופיע בין איברי הזוג. במקום לסמן $ f(x_{1},x_{2}) $ מסמנים $ x_{1}\star x_{2} $ כאשר $ \star $ הוא סימן מוסכם כלשהו שמסמן את פעולת $ f $.
פונקציה $ 3 $-מקומית נקראת פעולה טרינארית.
הרכבת פונקציות
 ערך מורחב – הרכבת פונקציות
ערך מורחב – הרכבת פונקציות
על קבוצה של פונקציות ניתן להגדיר פעולה בינארית בסיסית הקרויה הרכבת פונקציות. בהינתן פונקציה $ f\colon X\to Y $ ופונקציה $ g\colon Y\to Z $, מגדירים את ההרכבה שלהן $ h=g\circ f $ בתור פונקציה $ h\colon X\to Z $ המוגדרת לכל $ x\in X $ בתור $ h(x)=g(f(x)) $. כלומר תוצאת ההרכבה היא פונקציה המוגדרת על ידי הפעלת $ f $ על איבר ועל התמונה המתקבלת מפעילים את $ g $. הרכבת פונקציות אינה פעולה קומוטטיבית (לרוב $ f\circ g\neq g\circ f $ גם אם שני האגפים מוגדרים). עם זאת, זוהי פעולה אסוציאטיבית (כאשר יש שרשרת של פעולות הרכבה בזו אחרי זו, ניתן להוסיף בתוכה סוגריים היכן שרוצים בלי לשנות את התוצאה).
פונקציית הזהות היא איבר יחידה (שמאלי או ימני) ביחס להרכבת פונקציות. בהינתן פונקציה $ f\colon X\to Y $ מתקיים $ f\circ I_{X}=f $ וכן $ I_{Y}\circ f=f $. אם $ f $ הפיכה, אז מתקיים גם $ f^{-1}\circ f=I_{X} $ וכן $ f\circ f^{-1}=I_{Y} $.
מהתכונות שנמנו כאן נובע שקבוצת הפונקציות מקבוצה כלשהי $ X $ לעצמה (פונקציות מהצורה $ f\colon X\to X $) היא מונואיד ביחס לפעולת הרכבת הפונקציות. פונקציית היחידה $ I_{X} $ היא איבר היחידה (הדו-צדדי) של המונואיד. האיברים ההפיכים במונואיד הם הפונקציות ההפיכות.
קבוצת הפונקציות $ Y^{X} $
 ערך מורחב – חזקה: קבוצות
ערך מורחב – חזקה: קבוצות
את קבוצת הפונקציות מקבוצה $ X $ לקבוצה $ Y $ מסמנים $ Y^{X} $. סימון זה אינו מקרי. יש קשר הדוק בין קבוצה זו לפעולת החזקה.
לכל קבוצה יש עוצמה שניתן לתארה אינטואיטיבית כ"מספר האיברים" בה. העוצמות של קבוצות סופיות הן מספרים טבעיים. לקבוצות אינסופיות יש עוצמות אינסופיות, שעשויות להיות שונות זו מזו (תורת הקבוצות מבחינה בין גדלים שונים של אינסוף). את העוצמה של קבוצה $ X $ מסמנים $ |X| $.
אם $ X $ ו-$ Y $ הן קבוצות סופיות, אז מספר הפונקציות בקבוצה $ Y^{X} $ הוא מספר האיברים ב-$ Y $ בחזקת מספר האיברים ב-$ X $. בניסוח קומפקטי לפי הסימונים שהנהגנו זה עתה: $ \left|Y^{X}\right|=|Y|^{|X|} $. הזהות נובעת משיקול קומבינטורי פשוט שמסתמך על עקרון הכפל: נניח שבקבוצה $ X $ יש $ n $ איברים, ובקבוצה $ Y $ יש $ m $ איברים. נבחר איבר ראשון ב-$ X $, הוא יכול לעבור לכל אחד מ-$ m $ איברים. נבחר איבר שני ב-$ X $, גם הוא יכול לעבור לכל אחד מ-$ m $ איברים. וכן הלאה עד שנגיע לאיבר ה-$ n $ ב-$ X $. נכפיל את כל האפשרויות יחדיו לכל איברי $ X $ כדי לקבל את מספר האפשרויות הכולל ונקבל $ m^{n} $.
לקבוצות אינסופיות מחליטים לקבל זהות זו כהגדרה של חזקה בין עוצמות אינסופיות. לכל זוג עוצמות $ |X|,|Y| $ מגדירים $ |Y|^{|X|}=\left|Y^{X}\right| $. זוהי הגדרה מוצלחת, שכן היא מקיימת את חוקי החזקות והיא עדיין מהווה פעולת כפל מקוצר ביחס לכפל המוגדר בין עוצמות.
ראו גם
קישורים חיצוניים
- Calculus - Functions - הסבר על פונקציות

- פונקציה, באתר MathWorld (באנגלית)
- מה זאת פונקציה?, באתר לרגו
- פונקציה, באתר אנציקלופדיה בריטניקה (באנגלית)
| נושאים בתורת הקבוצות | ||
|---|---|---|
| מושגי יסוד | תורת הקבוצות הנאיבית • תורת הקבוצות האקסיומטית • קבוצה • יחידון • הקבוצה הריקה • קבוצת החזקה | |
| פעולות | איחוד • חיתוך • משלים • הפרש סימטרי • מכפלה קרטזית | |
| יחסים | יחס • יחס רפלקסיבי • יחס סימטרי • יחס אנטי-סימטרי • יחס טרנזיטיבי • יחס שקילות • יחס הופכי | |
| פונקציות | פונקציה • פונקציה חד-חד-ערכית • פונקציה על • פונקציה חד-חד-ערכית ועל • פונקציית הזיווג של קנטור | |
| משפטים | האלכסון של קנטור • משפט קנטור-שרדר-ברנשטיין • הלמה של צורן • משפט הסדר הטוב | |
| סדר | סדר חלקי • סדר מלא • סדר טוב • טיפוס סדר • מספר סודר | |
| עוצמות | עוצמה • קבוצה בת מנייה • קבוצה שאינה בת מנייה • עוצמת הרצף | |
| אקסיומות | אקסיומת ההיקפיות • אקסיומת האיחוד • אקסיומת הקבוצה האינסופית • אקסיומת ההחלפה • אקסיומת קבוצת החזקה • אקסיומת היסוד • אקסיומת הבחירה | |
| שונות | הפרדוקס של ראסל • השערת הרצף | |
פונקציה30848826