מספר ממשי

בערך זה |
במתמטיקה, מספר ממשי הוא מספר המייצג גודל, כמו או .
ניתן לראות את המספרים הממשיים החיוביים כאורכים של קטעים על ישר אינסופי (הקרוי, לפיכך, הישר הממשי). לכל מספר חיובי מתאים גם מספר שלילי באותו גודל, המודד את אותו קטע בכיוון ההפוך.
קיימת התאמה בין הישר הממשי למספרים הממשיים, כך שכל מספר ממשי מייצג נקודה אחת ויחידה על הישר הממשי וכל נקודה על הישר הממשי מייצגת מספר ממשי אחד ויחיד.
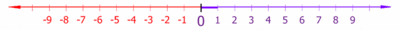
על המספרים הממשיים ניתן להגדיר פעולות חיבור וכפל שהופכות אותם למבנה אלגברי הקרוי שדה. שדה זה נקרא שדה המספרים הממשיים. בנוסף מוגדר על הממשיים יחס סדר טבעי לפי מיקומם על הישר הממשי. שתי תכונות אלו יחדיו הופכות את קבוצת המספרים הממשיים לשדה סדור שלם.

היסטוריה והתפתחות
השם "מספר ממשי" ניתן למספרים אלה במאה ה-17 על ידי דקרט, שעשה זאת כדי להבחין בין שורשים ממשיים לבין שורשים מדומים של פולינום.
בפיתוחו של החשבון האינפיניטסימלי במאה ה-18 נעשה שימוש נרחב במספרים ממשיים, אך ללא הגדרה נאותה שלהם. ב-1872 פרסם גאורג קנטור מאמר שבו הגדיר את המספרים הממשיים באמצעות סדרות קושי של מספרים רציונליים; הגדרתו (השקולה) של ריכרד דדקינד את המספרים הממשיים באמצעות חתכי דדקינד פורסמה מעט מאוחר יותר באותה שנה.
מספרים רציונליים ואלגבריים

לאחר שקובעים את אורכה של יחידה המידה היסודית, האורך של מספר יחידות כאלה נקרא מספר שלם. מספר ממשי שאפשר לבטא כיחס בין שני מספרים שלמים הוא מספר רציונלי, אך רוב המספרים הממשיים אינם כאלה - עוצמתה של קבוצת המספרים הממשיים היא עוצמת הרצף שאיננה בת מנייה (כפי שהוכח באמצעות האלכסון של קנטור), ואילו אוסף המספרים הרציונליים הוא בן-מנייה. המספרים הממשיים שאינם רציונליים, כגון שורש 2, או e, נקראים אי-רציונליים. את קבוצת המספרים האי-רציונליים אפשר לחלק לשתי תת-קבוצות:
- קבוצת המספרים האלגבריים: מספרים המהווים שורש של פולינום בעל מקדמים רציונליים (או שלמים, אין הבדל). זו קבוצה בת מנייה.
- קבוצת המספרים טרנסצנדנטיים: מספרים שאינם מספרים אלגבריים. זו קבוצה שאינה בת מנייה ועוצמתה היא עוצמת הרצף. קיומם של מספרים טרנסצנדנטיים הוכח לראשונה בשנת 1844 על ידי המתמטיקאי הצרפתי ז'וזף ליוביל והתוצאה קרויה על שמו משפט ליוביל. בשנת 1882 הוכיח פרדיננד לינדמן את משפט לינדמן שקובע, בין השאר, ש־ (פאי) הוא מספר טרנסצנדנטי.
לכל מספר ממשי אי-שלילי יש שורש ריבועי ממשי, ולכל מספר ממשי שלילי אין שורש ריבועי ממשי. למספרים שליליים יש שורש מדומה. למעשה, השורשים באים בזוגות: אם אז שניהם שורשים ממשיים של ואם אז שניהם שורשים מדומים של . באופן כללי, הפתרון של משוואה ריבועית הוא שני מספרים מרוכבים (כולל ריבוי). כל מספר ממשי הוא גם מספר מרוכב.
ההצגה העשרונית
כל מספר ממשי אפשר להציג כשבר עשרוני, בעל מספר סופי או אינסופי של ספרות מימין לנקודה.
- לחלק מהמספרים הרציונליים הייצוג כשבר עשרוני הוא סופי (למשל: 0.5=1/2), ולאחרים - אינסופי מחזורי, למשל: ...0.08536585365=7/82 (מחזור בן 5 ספרות),
- מספרים שהם שברים עשרוניים סופיים ניתנים להצגה כשברים אינסופיים בשתי דרכים:
- למספרים האי-רציונליים הייצוג כשבר עשרוני אינו מחזורי. למשל, הוא מספר טרנסצנדנטי, והייצוג העשרוני שלו אינו מחזורי. חמישים הספרות הראשונות הן . לצרכים מעשיים ניתן להסתפק בדיוק נמוך יותר, ומקובל להסתפק בקירוב 3.14.
מרחק וטופולוגיה

בטופולוגיה, קבוצת המספרים הממשיים יוצרת מרחב מטרי, שבו המרחק בין ל- מוגדר כערך המוחלט . בדרך זו התאמתם של המספרים הממשיים לנקודות על הישר הממשי מאפשרת לבטא את אורכו של כל קטע במישור.
על פי תכונת ארכימדס, לכל מספר ממשי קיים מספר טבעי שגדול ממנו. נובע מכאן שהמרחב המטרי של המספרים הממשיים הוא מרחב ספרבילי, משום שקבוצת המספרים הרציונליים, שהיא בת מנייה, היא קבוצה צפופה (שכן כל קטע פתוח מכיל מספר רציונלי). הארכימדיות מאפשרת להגדיר את הערך השלם של , בתור המקסימום של .
ראו גם
קישורים חיצוניים
- גדי אלכסנדרוביץ', מהם המספרים הממשיים?, באתר "לא מדויק", 7 בספטמבר 2010
- מספר ממשי, באתר MathWorld (באנגלית)
- מספר ממשי, באתר אנציקלופדיה בריטניקה (באנגלית)
| מערכות מספרים | ||
|---|---|---|
| מספרים | המספרים הטבעיים (מערכת פאנו) • חוג המספרים השלמים (מספרים חיוביים ושליליים, מספר שלם) • שדה המספרים הרציונליים (מספר רציונלי, מספר אי-רציונלי) • שדה המספרים הממשיים (הישר הממשי, מספר ממשי) • שדה המספרים המרוכבים (המישור המרוכב, מספר מרוכב, מספר מדומה) | |
| הרחבות של חוג המספרים השלמים | חוג השלמים של גאוס • חוג השלמים האלגבריים • חוג השלמים של אייזנשטיין | |
| הרחבות של שדה המספרים הרציונליים | שדה מספרים • שדה המספרים הניתנים לבנייה • שדה המספרים האלגבריים (מספר אלגברי, מספר טרנסצנדנטי) • שדה המספרים ה-p-אדיים (מספר p-אדי) • שדה ציקלוטומי | |
| מעבר למרוכבים | אלגברת קווטרניונים (אלגברת הקווטרניונים של המילטון ) • אלגברת אוקטוניונים (אלגברת האוקטוניונים של קיילי ) • אלגברות קיילי-דיקסון | |
מספר ממשי37645936Q12916


