היסטוריה של האריתמטיקה

האריתמטיקה נכללת עם שבע האמנויות החופשיות ונתפסה בעבר, ואף כיום, כחלק בסיסי מהידע של כל אדם משכיל. ניתן למצוא את הדמות המסמלת את האריתמטיקה בפינה התחתית-שמאלית של התמונה כאשר היא עסוקה במניית חפצים. לצדה הדמות המייצגת את הגאומטריה כשהיא עסוקה במדידת זווית. בפינה הימנית-עליונה מופיעה הדמות המייצגת את האסטרונומיה כשהיא צופה בכוכבים, ובשמאלית-עליונה דמות המציגה את הדקדוק בדמות מורה המעניש את תלמידו. לא אחת, היו ההתפתחויות באסטרונומיה ובגאומטריה מובילות להתפתחויות באריתמטיקה, ולהיפך.

האריתמטיקה היא הענף העתיק ביותר במתמטיקה ואחד השימושיים שבו לצורכי יום-יום. ההיסטוריה של האריתמטיקה משתרעת על פני תקופות שונות, תרבויות ומקומות שונים בהם התפתח ענף זה. בחלק מהמקרים היו אלה התפתחויות שנצברו על סמך ניסיון רב-שנים ובחלק מהמקרים היו אלה פירות מחקר של מתמטיקאים. עד לעת החדשה התפתחה האריתמטיקה באופן שונה באזורים גאופוליטיים שונים, ולפיכך כרוכה היסטוריה זו גם בהיסטוריה הדתית, החברתית והגאופוליטית של מקומות אלה. כך, למשל, עם כיבוש הבבלים את מסופוטמיה, ירשו אלה את השימוש בבסיס 60 מקודמיהם השומרים. כדוגמה נוספת, רוחבית, ניתן להסתכל על מושג האפס. פיתוחו, כפי שהוא מוכר היום, עבר שלבים רבים והושפע רבות מהקשיים התפיסתיים, הדתיים והפילוסופיים שעורר בתרבויות השונות; מתפקידו כ"מקום ריק" למספר עצמאי בעל תכונות מיוחדות עבר האפס גלגולים ופיתוחים שונים.

במקביל לשינויים בתחומים המוזכרים לעיל, לרוב לוותה ההתפתחות המדעית בתחום האריתמטיקה בהתפתחויות מתחומי מדע אחרים, בעיקר אסטרונומיה וענפים אחרים של המתמטיקה. כך למשל, הצורך להכפיל פי שניים את שטחו של מזבח, שהוא בעיה גאומטרית, גרר צורך לחשב את השורש הריבועי של שתיים.

עם ההתקדמות המדעית והטכנולוגית, ובכללה מהפכת הדפוס, נוצר צורך ליצירת "שפה מתמטית אחידה". כך, התקבעו סימונים, הגדרות ואלגוריתמים מוסכמים המשמשים את רוב העולם המודרני, כדוגמת מערכת הספרות ההודיות-ערביות והשיטה העשרונית. עם ההתפתחויות במחשוב נכנסו לשימוש, במקביל למערכות אלה, מערכות נוספות כגון מערכת הספירה הבינארית וההקסדצימלית.

במתמטיקה המודרנית אין אחדות לגבי המונח "אריתמטיקה" והוא משמש לא אחת גם לתיאור נושאים משיקים או קרובים כדוגמת תורת המספרים וגאומטריה אלגברית או אריתמטיקה גאומטרית.

מצרים העתיקה

ערך מורחב – ספרות מצריות

העדויות הראשונות לביצוע פעולות מורכבות בתחום המתמטיקה בכלל והאריתמטיקה בפרט הן ממצרים העתיקה. החברה המצרית הייתה מורכבת ומפותחת, והשפע שנוצר בה אִפשר לה לקדם פרויקטים מעשיים ומחקר, שהביאו להתקדמות מדעית שנכנסה לשימוש לתועלת הממלכה. כך, למשל, חלק מן ההתפתחויות בתחום האסטרונומיה אפשרו תכנון חקלאי מדויק יותר. כעדות להישגים הטכנולוגיים אשר התאפשרו משליטתם של המצרים במתמטיקה ובהנדסה, ניתן לראות את בנייתה של הפירמידה הגדולה של גיזה בשנת 2740 לפנה"ס.

המצרים השתמשו בשיטת ייצוג מספרים שהתבססה על החזקות של 10, מ-1 ועד מיליון, שיוצגו על ידי סמלים נפרדים. מספרים נכתבו כצירוף סמלים שייצג סכום של חזקות אלה, ללא חשיבות לסדר הסמלים.

יש מספר ממצאים כמו פפירוס מוסקבה (1850 לפנה"ס) ופפירוס רינד (1650 לפנה"ס), המעידים על פתרון משוואות לינאריות וריבועיות, אך בכל הממצאים ניכר כי המצרים השתמשו באריתמטיקה כמדע שימושי.

בבל

הספרות הבבליות – ניתן להבחין בנקל בשיטת הקיבוץ המשנית בה השתמשו הבבלים

בסביבות שנת 3500 לפנה"ס שלטו באזור מסופוטמיה השומרים, שעשו שימוש בכתב יתדות וערכו את חישוביהם בבסיס 60. בין השנים 2300 ל-2100 לפנה"ס שלטו באזור זה האכדים, שהשפיעו על התרבות האשורית. הם הביאו עמם, בין היתר, את הגרסה שלהם לכלי המוכר לנו כיום יותר בתור החשבונייה. בשנת 1900 לפנה"ס, אחרי שפלשו למסופוטמיה, קבעו הבבלים את בירתם בבבל. סביר להניח כי הבבלים ירשו את שיטת הספירה שלהם מן האשורים והאכדים משום נוחיותה. להשערות בדבר בחירת המספר 60 כבסיס ראו ערך בסיס סקסגסימלי.

שיטת הספירה הבבלית הביאה עמה חידוש משמעותי ביחס לשיטות הקודמות לה: הבבלים קישרו בין מיקומה של הספרה לבין הגודל שהיא מייצגת, בדומה לשיטה העשרונית בימינו כאשר בסיס הספירה הוא, כאמור, 60. כדי למנוע את הצורך ביצירת 60 סימנים מוסכמים שונים, השתמשו הבבלים בספירת משנה קיבוצית (ראו תמונה).

החידוש המשמעותי בהכנסת שיטה זו לשימוש הוא בקיצור ההצגה של מספרים גדולים. בשיטות שהן קיבוציות בלבד יש צורך בסימנים רבים על מנת להציג מספרים מסוימים (לדוגמה, 1999 נכתב ב-7 סימנים בשיטה הרומית וב-28 סימנים בשיטה המצרית) בעוד שמספרים קרובים אליהם נכתבים בקיצור (2000 נכתב בשני סימנים בלבד בשיטות אלה). לעומת זאת, בשיטות הכוללות קישור בין מיקום הספרה לסדר הגודל שלה, מספר הספרות הדרושות להצגת המספר קטן יותר ברוב המקרים, ומספרים קרובים זה לזה דורשים אותו מספר של ספרות. פרט לחסכון בכתיבה, מספר הספרות נותן מושג מקורב על גודלו של המספר (ֹסדר גודל).

היעדר ספרה המייצגת את המספר 0 גרם לבבלים, במשך תקופה ארוכה, להשאיר רווח בכל מקום בו נדרש הסימון המייצג 0. סימן מתאים נכנס לשימוש בספרות הבבליות רק בשלב מאוחר יותר.

לשיטה זו השפעה על האריתמטיקה המוכרת לנו כיום בשני מישורים עיקריים: ראשית – בהכנסת עקרון המיקום כחלק משיטת הספירה, עיקרון המאפשר קיצור הצגת מספרים גדולים והערכת סדר גודל, שנית – בשימוש שאנו עושים היום בבסיס 60; חלוקת השעה ל-60 דקות וחלוקת המעגל ל-360 מעלות הן השפעות של השימוש בשיטה הבבלית.

בטבלאות אשר נמצאו על הפרת ומתוארכות לשנת 2000 לפנה"ס נמצאו ריבועי המספרים עד 59 וחזקותיהם השלישיות של המספרים עד 32. הבבלים עשו שימוש בזהויות $\ ab={\frac {[(a+b)^{2}-b^{2}-a^{2}]}{2}}$ או $\ ab={\frac {(a+b)^{2}-(a-b)^{2}}{4}}$ ובטבלאות המתוארות לעיל כדי לפשט את חישוביהם. לבבלים לא היה אלגוריתם לחילוק ארוך, לכן השתמשו בעובדה שמתקיים ${\frac {a}{b}}=a\times {\frac {1}{b}}$ ובטבלה של מספרים הופכיים. בטבלאות אלה לא נכללו שברים שמכניהם 7 ו-11 (שפיתוחיהם בבסיס 60 הם אינסופיים), אך נכללו קירובים עבור המכנים 59 ו-61 (שפיתוחיהם אינסופיים עם מחזוריות פשוטה).

פלימפטון 322 הוא ממצא ארכאולוגי המדגים את הרמה המתמטית שאליה הגיעו הבבלים. זהו לוח חרסית שמקורו בבבל והוא מתוארך בין השנים 1900 לפנה"ס עד 1600 לפנה"ס. הפרשנויות לגבי לוח זה חלוקות. על פי חלק מהפרשנויות, הלוח שימש לייצור שלשות פיתגוריות או לחישוב ערכיה של פונקציה טריגונומטרית ובכך הוא מעיד על רמה מתמטית גבוהה של התרבות הבבלית ומתבלט ביחס לשאר הממצאים מסוגו. על פי פרשנות אחרת, הלוח שימש כלי עזר בהוראת חשבון, ואין בו ייחוד רב ביחס לממצאים הדומים לו.^{[דרושה הבהרה]}

יוון העתיקה

כריכת ספרו של דיופנטוס "אריתמטיקה" משנת 1621 בתרגום ללטינית.

ערך מורחב – מתמטיקה ביוון העתיקה

היוונים היו הראשונים שפיתחו את האריתמטיקה המחקרית, במאה ה-6 לפנה"ס, בניגוד לבבלים, לסינים ולמצרים שראו באריתמטיקה כולה בבחינת מדע שימושי. כבר בימי פיתגורס (המאה ה-6 לפנה"ס), התקיימה אצל היוונים גישה דומה ביותר לגישה המודרנית לאריתמטיקה. היוונים השתמשו במערכת אקסיומות כדי לבסס את חישוביהם, התעניינו במהות המספרים הפילוסופית, מיינו את המספרים לסוגים שונים, וחקרו את תכונותיהם הכלליות. כמו כן, היוונים היו הראשונים שהוכיחו שישנם אינסוף מספרים ראשוניים (ראו קיומם של אינסוף מספרים ראשוניים), כשהראשון שהציג הוכחה לכך בכתב היה אוקלידס בספרו "יסודות", ולהלן ההוכחה מסִפרו:

נניח שיש רק מספר סופי של מספרים ראשוניים. ניקח את כל הראשוניים הללו, נכפיל אותם זה בזה ונוסיף 1. התוצאה שקיבלנו נותנת שארית 1 בחלוקה לכל אחד מהמספרים הראשוניים. לכן תוצאה זו אינה מתחלקת באף אחד מהראשוניים – היא חייבת להיות מספר ראשוני נוסף, או להתחלק במספר ראשוני שאינו ברשימת המספרים הראשוניים שלנו. בכל מקרה קיבלנו שההנחה שיש מספר סופי של ראשוניים מובילה לסתירה, ולכן הנחה זו אינה נכונה, כלומר יש מספר אינסופי של ראשוניים.

— אוקלידס, יסודות

היוונים סללו את הדרך למציאת הוכחה למשפט היסודי של האריתמטיקה.

ניתן לומר שהפיתגוראים גילו את היותו של השורש הריבועי של 2 אי-רציונלי, אך תגליתם הייתה למעשה רק שהקטעים הם חסרי מידה משותפת, והתכונה אי-רציונליות התגלתה מאוחר יותר. אזכור ראשון לקיומם של קטעים חסרי מידה משותפת מופיע בדיאלוג "תאיטיטוס" של אפלטון, אך רעיון זה היה מוכר עוד קודם לכן, במאה החמישית לפנה"ס להיפאסוס, בן האסכולה הפיתגוראית, ואולי לפיתגורס עצמו.

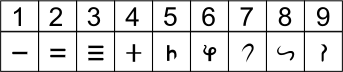
כדי לייצג מספרים בכתב, היוונים השתמשו תחילה במערכת מספרים המבוססת על כפולות של חזקות של 10, כאשר הסמל של כל מספר היה האות הראשונה של אותו מספר באלפבית היווני. למשל, המספר 5 (ביוונית: Πέντε) סומל באות π. כפולות של חזקות של 10 הוצגו בעזרת סמל המספר הכופל ואחריו סמל החזקה, כמפורט בטבלה להלן. מספר שהיה מורכב מיותר מכפולה אחת של חזקה של 10 הוצג כסכום. שיטה זו נקראה השיטה האטית, על שם האזור בו התפתחה - אטיקה.

האותיות בהם השתמשו היוונים כמספרים בשיטה האטית:

המספר:	50,000	10,000	5,000	1,000	500	100	50	10	5	1
הסימן:	πμ	μ	πχ	χ	πη	η	πδ	δ	π	ι
שמו היווני:	πεντάκις μύριοι	μύριοι	πεντάκις χίλιοι	χίλιοι	πενταόσιοι	έκαου	πέντήκοντα	δέκα	πέντε	εϊξ

האותיות בהם השתמשו היוונים כמספרים בשיטת ה"גרשים":

המספר:	9	8	7	6	5	4	3	2	1
הסימן:	θʹ‎	ηʹ‎	ζʹ‎	ϝʹ‎	εʹ‎	δʹ‎	γʹ‎	βʹ‎	αʹ‎
המספר:	90	80	70	60	50	40	30	20	10
הסימן:	ϟʹ‎	πʹ‎	οʹ‎	ξʹ‎	νʹ‎	μʹ‎	λʹ‎	κʹ‎	ιʹ‎
המספר:	900	800	700	600	500	400	300	200	100
הסימן:	ϡʹ‎	ωʹ‎	ψʹ‎	χʹ‎	φʹ‎	υʹ‎	τʹ‎	σʹ‎	ρʹ‎

בתקופה מאוחרת יותר השתמשו היוונים בשיטת סימון מתקדמת יותר, שבה הוצגו המספרים לפי האלפבית היווני. בשיטה זו השתמשו ב-26 האותיות היווניות, כאשר לסימון המספרים בין 1 ל-9 נקבעו תשע האותיות הראשונות (דאז, כאשר האות ϝ הייתה בשימוש), בתוספת גרש ( ' ) בצד ימין של האות, למעלה. תשע האותיות הבאות ייצגו את העשרות מ-10 עד 90, והבאות את המאות. לסימון הספרות בין 1000 ל-900,000, השתמשו היוונים באותן אותיות, אך הוסיפו לאותיות את הגרש דווקא מצד שמאל של האותיות, למטה. ממיליון ומעלה, כנראה^{[דרושה הבהרה]} השתמשו היוונים בשני תגים במקום אחד.

אחד המתמטיקאים היוונים החשובים ביותר היה דיופנטוס, שחיבר במאה ה-3 לספירה את ספרו "אריתמטיקה" שנחשב המקביל האריתמטי-אלגברי ל"יסודות" של אוקלידס. בספר זה הציג דרכים לפתירת מערכת משוואות אשר מספר הנעלמים בהן גדול ממספר המשוואות ופתרונותיהם הם מספרים שלמים בלבד. משוואות כאלה קרויות על שמו משוואה דיופנטית. בזכות יצירה זו מכונה דיופנטוס בשם "אבי האלגברה".

הדמויות הבולטות בתקופה זו היו פיתגורס מהאי סמוס, הזכור בעיקר בשל משפט פיתגורס והאסכולה הפיתגוראית שעסקה בנומרולוגיה, אוקלידס מחבר הספר "יסודות", שהיה הספר המרכזי ללימוד הגאומטריה במשך מאות רבות וארכימדס מסירקוסאי, שהמציא בין השאר שיטת ספירה עבור מספרים גדולים, והגיע עד ל- $\ 10^{8\cdot 10^{16}}$.

מלבד התרומה של המתמטיקאים היווניים לגיבוש וארגון התחומים שבהם עסקו, יש לציין את פיתוח התאוריה של חתכי חרוט, שנולדה במהלך התקופה ההלניסטית, והתפתחה ללא שימוש מפורש באלגברה או בטריגונומטריה. המתמטיקה הגיעה לרמה כזו, שאפשרה לתלמי לנסח מודל גיאוצנטרי של מערכת השמש, שהיה בשימוש עד למאה ה-17.

רומא העתיקה

שיחזור של אבקוס רומי עשוי ברונזה, הנמצא באוניברסיטת מיינץ אשר בגרמניה.

תרומתם של הרומים לאריתמטיקה איננה התפתחות מתמטית חשובה, אלא הכנסת השימוש בספרות רומיות והגדרת האריתמטיקה כחלק חשוב מ"סל הכלים" של האדם המלומד, כפי שניתן לראות בהכללתה בשבע האומנויות החופשיות. בספרות הרומיות השתמשו בכל רחבי אירופה, עד שהוחלפו בספרות ההודיות-ערביות, בשל פשטותן ונוחות השימוש בהן ביחס לשיטה הרומית.

השיטה הרומית מבוססת על הקבצה - כל מספר מיוצג כאוסף של סימנים, כאשר כל אחד מהסימנים מייצג כמות קבועה מראש, למרות שהיא כן תלויה במיקומו במספר. ערכו של המספר נקבע על פי סכום ערכי הסימנים המופיעים, כאשר חלק מהסימנים עשויים להיות מחוסרים מהסכום, בהתאם למיקומם במילה.

שיטת הספרות הרומיות מכילה שבעה סימנים בסיסיים שמקורם באלפבית הלטיני:

I, המייצגת את הספרה אחת, ובשפת המקור unus.
V, המייצגת את הספרה חמש, ובשפת המקור quinque.
X, המייצגת את הספרה עשר, ובשפת המקור decem.
L המייצגת את הספרה חמישים, ובשפת המקור quinquaginta.
C המייצגת את הספרה מאה, ומקורה כנראה במילה centum שפירושה מאה.
D המייצגת את הספרה חמש מאות, ובשפת המקור quingenti.
M המייצגת את הספרה אלף, ומקורה כנראה במילה mille anangu שפירושה אלף.

למספרים גדולים השתמשו הרומאים בקו עליון מעל הספרה, המסמל למעשה את הכפלתה ב-1,000.

דוגמאות:

V =‏ 5,000.

X = 10,000.

בכתיבת מספר, הספרות נרשמות משמאל לימין, מהגדולות לקטנות. אם מופיעה ספרה קטנה משמאל לספרה הגדולה ממנה, יש לחסר את הספרה הקטנה מהמספר הכולל. למשל:

• V מסמל את המספר 5.
• IV מסמל את המספר 4 - המספר 5 שמסומל על ידי V, פחות המספר 1 שמסומל על ידי I ומופיע משמאל ל-V.
• VI מסמל את המספר 6: כאשר I מופיע מימין ל-V, ולכן הוא אינו מחוסר מהמספר הכולל אלא מחובר אליו.
• 23 מסומן ב-XXIII שהוא צירוף של X+X+I+I+I.

מטרת החיסור היא לפשט צירופים: במקום לכתוב IIII עבור 4, די לכתוב שתי ספרות: IV.

השימוש בשיטת החיסור נעשה עבור הספרות הבאות: I יכול להופיע משמאל ל-V או ל-X .X יכול להופיע משמאל ל-L או ל-C, ו-C יכול להופיע משמאל ל-D או ל-M.

בעת העתיקה השימוש בשיטת החיסור היה מקובל פחות מאשר בימינו, ועל כן לרוב השתמשו ב-IIII על מנת לייצג 4, ולא ב-IV, וכדומה.

הספרות הרומיות נותרו לשימוש בעיקר כאמצעי דקורטיבי, למשל בשעונים. בנוסף, הן מופיעות גם בטקסטים רשמיים כגון חוקת ארצות הברית.

התרבות ההודית

תרומתם העיקרית של ההודים לאריתמטיקה היא פיתוח השיטה העשרונית והכנסת שימוש מלא במושג אפס, כמו גם עבודתם עם מספרים שליליים.

בין השנים 2500 לפנה"ס ל-1700 לפנה"ס התקיימה בהודו תרבות עמק האינדוס. אנשי תרבות זו אימצו מערכת של מידות ומשקולות המבוססת על חלוקה עשרונית של "מידות טבעיות". בחפירות ארכאולוגיות נמצאו שרידים המראים על שימוש ביחידת מידה של 3.35 ס"מ אשר מהווה באורכה עשירית מיחידת הרגל. ממצאים אחרים הראו על שימוש ביחידת מידה שאורכה 0.932 ס"מ ומהווה מאית מיחידת הפסע. מדידות באתרים ארכאולוגיים הראו כי יחידות אלה היו בשימוש לצורכי בנייה.

עם ירידת קרנם של תושבי עמק האינדוס, תפסו את מקומם ההינדו-אריאנים. ספרי הקודש שלהם, הודה, כללו בין היתר את ה"שולבה סוטרא" - ספר קודש המתאר בניית מזבחות המיועדים להקרבת קרבנות. בספר זה מובאים משפטים ללא הוכחות המתארים, למשל, בניית מזבח רבוע ששטחו זהה לזה של משולש נתון או בניית מזבח רבוע ששטחו זהה בקירוב לזה של מעגל נתון. בחישוביהם היה עליהם למצוא את ערכו של ${\sqrt {2}}$, ככל הנראה על מנת לפתור בעיות הנוגעות להכפלת שטחו של מזבח רבוע. בשולבה סוטרא נתן הסבר זה לחישוב ערכו:

הגדל יחידת אורך בשליש ושליש זה ברבע ממנו והחסר מכך את החלק השלושים וארבע של הרבע האמור.

— השולבה סוטרה

ובכתיב מתמטי ${\sqrt {2}}\approx 1+{\frac {1}{3}}(1+{\frac {1}{4}}(1-{\frac {1}{34}}))={\frac {577}{408}}\approx 1.4142156$. הקירוב מדויק עד הספרה החמישית אחרי הנקודה (זהו השבר הקרוב ביותר ל-$\ {\sqrt {2}}$ מבין כל השברים שהמכנה שלהם קטן מ-985). לא ידוע לנו כיום כיצד הושג דיוק מרשים זה, אך ישנן מספר השערות בנושא.

גרסה של ספרות ברהאמיניות כפי שהיו מקובלות במאה הראשונה לפנה"ס

בערך בסביבות המאה השלישית לפנה"ס, החלו להופיע הספרות הברהאמיניות (ראו איור). ספרות אלה הן היסוד לספרות המוכרות לנו כיום מהשימוש בשיטה העשרונית. הסימנים המוכרים לנו כיום התקבעו במאה החמש-עשרה, בין היתר הודות לצורך במערכת מוסכמת שבא בעקבות מהפכת הדפוס. ישנן מספר השערות בנוגע לדרך בה אימצו ההודים את השילוב של בסיס עשרוני עם העקרון של סדר גודל התלוי במיקום הספרה. השערה אחת מתבססת על העובדה שהראשונים לקשר בין מיקום הספרה לסדר הגודל שלה היו הבבלים. לפי השערה זו, העיקרון הועבר להודים על ידי היוונים כאשר ההודים "שילבו" אותו עם השימוש בבסיס ספירה עשרוני. השערה אחרת רואה בפיתוח התבססות על השיטה הסינית. השערה שלישית טוענת כי ההודים הגיעו לרעיון זה לבדם ללא גורם מתווך.

על חשיבותה של שיטת הספירה ההודית אמר פייר סימון לפלס את הדברים הבאים:

השיטה המבריקה שבעזרתה ניתן לבטא כל מספר בעזרת 10 סימנים בלבד (כשלכל סימן סדר גודל וגודל מוחלט) מקורה בהודו. בימינו רעיון זה נראה כה פשוט עד שחשיבותו ונחיצותו אינם מוערכים דיו. חשיבותו נעוצה בכך שפישט את החישובים והציב בכך את האריתמטיקה בכפיפה אחת עם ההמצאות השימושיות ביותר. חשיבותה של המצאה זו מתבהרת עוד יותר כאשר אנו חושבים על כך שהייתה מעבר להישג-ידם של הקדמונים הגדולים כדוגמת ארכימדס ואפולוניוס.

עם ירידת קרנה של הדת ההודית, החלו דתות אחרות לבסס את מעמדן. אחת מהן, הייתה הג'ייניזם שהתפתחה במאה השישית לפני הספירה, על בסיס ההינדואיזם. הקוסמולוגיה הג'יינית והצורך בתחזיות אסטרונומיות (לכתיבת לוחות שנה, למשל) היוו כוח מניע להתפתחויות מתמטיות רבות. עם זאת, המתמטיקה נתפסה עדיין כמדע שימושי או ככלי יישומי. כך, למשל, הביאו סוגיות בקוסמולוגיה פיתוח רעיונות בנושא האינסוף שלא נשקלו בשנית עד לעבודותיו של גיאורג קנטור.

בערך בשנת 500 לספירה פרסם המתמטיקאי ההודי אריאבהטה את עבודתו אשר כללה סיכום של ידע רב במתמטיקת הג'יין והצגה של מספר רעיונות מהפכניים ביחס לאותה תקופה באסטרונומיה. בכך נחשבת עבודתו למבשרת העידן הקלאסי של המתמטיקה ההודית. בין היתר, ביסס אריאבהטה תאוריה מדעית לביסוס התופעות של מופעי הירח וליקויי מאורות. בעבודותיו שילב טריגונומטריה ופתרון משוואות. פיתוח עבודותיו נמשך רבות גם אחרי מותו. תקופת "העידן הקלאסי" במתמטיקה ההודית הביאה עמה שכלולים וחידושים בתחומים רבים, בהם גם שכלול של שיטת הספירה ההודית.

במאה השתים עשרה בוצעו מספר התקדמויות חשובות בתחום, חלק ניכר מהן על ידי המתמטיקאי ההודי בהסקרה השני, שבספרו מוצעות ארבע שיטות לביצוע כפל ארוך. הוא דן גם בנושאים אחרים כמו מספרים חיוביים ושליליים, האפס וחילוק באפס, בעיות העוסקות בכפל ובחילוק, ונושאים באלגברה ובטריגונומטריה.

כבר בתחילת המאה ה-12 ידעו ההודים להבדיל בין שני ערכי השורש הריבועי של מספר חיובי (זה השלילי וזה החיובי) ופיתחו כללים קבועים לארבע פעולות חשבון, כדוגמת הכלל הקובע כי מכפלת שני מספרים שווי סימן תהא חיובית ואילו מכפלת שני מספרים שוני סימן תהא שלילית.

סין

חשבונייה סינית.

עקב סיבות גאופוליטיות, במשך שנים רבות התפתחה התרבות של סין העתיקה עם זיקה מעטה מאד לתרבויות אחרות. המתמטיקה הסינית, בשונה מהמתמטיקה היוונית, הייתה מתמטיקה תכליתית. מחקר מתמטי תאורטי היה מועט למדי בסין העתיקה.

מעט מאד ידוע על המתמטיקה הסינית עד למאה הראשונה לפני הספירה. הספר החשוב ביותר אשר השתמר בידינו מתקופה זו הוא ה"גּ'וֹּבִּי סְוַּאנְגִּ'ינְגּ" - "המדריך של ג'ואו למדידת צללים" - אשר מתוארך לתקופה של 100 לפנה"ס עד 100 לספירה ואשר נמנה עם "עשר הקלאסיקות". ספר זה עוסק במדידת מיקומם של גופים שמימיים, אך המתמטיקה שבו שימושית אף לצרכים אחרים. ספר זה מכיל את "משפט גאוגו" אשר מהווה גרסה סינית ל"משפט פיתגורס".

הספר הנחשב לחשוב ביותר בהיסטוריה המתמטית של סין הוא "גְּ'יו גַּ'אנְגּ סְוַּאן שוּ" - "תשעת הפרקים של אמנות המתמטיקה" המכיל מידע שנאסף במשך שנים רבות ונחשב לאבן-דרך בהתפתחות המתמטית של סין ספר זה מכיל 246 בעיות מתחומי חיים שונים האמורות להקיף את הידע הדרוש לפתרון בעיות מתמטיות יום-יומיות. בספר זה מתוארות נוסחאות ושיטות חישוב המובאות ללא הוכחה. בפרק הראשון, העוסק במדידת שטחים, ישנם הסברים על ביצוע ארבע פעולות חשבון על שברים, כמו גם את האלגוריתם האוקלידי למציאת מחלק משותף מקסימלי. בפרק השני, העוסק בסחר בטובין, מובאות דוגמאות לשימוש בחוקי הפרופורציות והאחוזים. הפרק השלישי העוסק בסוגי חלוקה; ישנו שימוש בחוקי פרופרציות, הן ישרות והן הפוכות והן שימוש בטורים חשבוניים והנדסיים. הפרק הרביעי עוסק בבעיות שבהן ישנה תלות בין אורך לשטח ועוסק ביישומים של נושאים כגון שברי יחידה ושורשים מסדר שני ושלישי. בפרק זה ניתן למצוא את רעיון הגבול והאינפיניטסימל. הפרק החמישי עוסק בהנדסה אזרחית ובנושאים של הנדסת המרחב. הפרק השישי עוסק בבעיות המשלבות נושאים כמו קצב ופרופורציה. בעיות בסגנונה של "בעיה מספר 26" נפוצות עד לימינו:

מקווה מוזן על ידי חמש תעלות. דרך התעלה הראשונה לבדה יוזן המקווה בשליש יום, דרך השנייה לבדה ביום, דרך השלישית לבדה ביומיים וחצי, דרך הרביעית לבדה בשלושה ימים ודרך החמישית לבדה בחמישה ימים. לו תחוברנה כל התעלות בו-זמנית למקווה, כמה זמן יקח לו להתמלא?

— "תשעה פרקים של אמנות המתמטיקה"

בפרקים השביעי והשמיני ניתן למצוא דרכים לפתרון משוואות לינאריות. הפרק התשיעי עוסק במשולשים ישרי זווית וכולל יישומים של משפט פיתגורס, שלשות פיתגוראיות וחפיפת משולשים. בפרק זה ניתן למצוא משוואות ריבועיות כדוגמת $\ x^{2}+34x=7100$ ואת פתרונן באמצעות האלגוריתם הסיני להוצאת שורש ריבועי, ולא באמצעים אלגבריים.

בספרו של שְׂיָאהוֹאוּ יָאנְג (חי בערך בין השנים 400 ל-470) "המדריך של שְׂיַאהוֹוּ יַאנְגּ למתמטיקה" נתן למצוא הצגות עשרוניות למספרים תוך שימוש בחזקות חיוביות ושליליות. במדריך אחר מאת גַּ'אנְגּ צְ'יוֹגְּ'יֵן נתן למצוא נוסחה לסכום של טור חשבוני. האסטרונום דְּזוּ צ'ונְגּ-גְּ'ה (429-501), בעזרת בנו, הוכיח כי ערכו של π נמצא בין 3.1415926 לבין 3.1415927. הוא המליץ להשתמש בקירוב 355/113 עבור עבודות מדויקות ובקירוב 22/7 עבור עבודות מדויקות פחות.

וַּאנְגּ שְׂיַה טונְגּ (580–640 בקירוב) כתב את "האריתמטיקה על בסיס הכללים העתיקים", עבודה בת 20 בעיות בלבד שכולן בעיות מדידה. בעבודה כלולה מתמטיקה מתקדמת למדי ביחס לתקופתה, כולל משוואות ממעלה שלישית, וניתן לראות בה את ראשית האלגברה הסינית.

התפתחויות חשובות נוספות בתחום האריתמטיקה בוצעו על ידי גְּ'יַה שְׂיֵן (חי בערך בין 1010 לספירה לבין 1070) אשר שכלל את הדרכים למציאת שורשים מרובעים ושורשים קוביים.

תרבות המאיה

המספרים מ-0 ועד 19, בספרות המאיה

תרבות המאיה התקיימה במרכז אמריקה. התור הקלאסי של תרבות המאיה התקיים בין השנים 250 ל-900 לספירה. העיר טיקאל בחצי האי יוקטן הגיעה בשיאה לאוכלוסייה של כ-50,000 תושבים ועם כ-3,000 מבנים. כוהני הדת של תרבות המאיה עסקו רבות באסטרונומיה והיו בעלי השפעה רבה על תרבות המאיה בכללותה. לפיכך, כפועל יוצא, היה צורך בכלים מתמטיים לשם בניית לוחות שנה ולניבויים אסטרונומיים. לצורך זה פיתחו בני המאיה מערכת ספרות מתקדמת יחסית לתקופתם.

בני המאיה השתמשו בספרות המאיה שפיתחו, שהתבססו על בסיס 20, ככל הנראה מתוך ספירה על ידי שימוש באצבעות הרגליים והידיים גם יחד. אחד משלושת הסימנים מייצג את המספר 5, ככל הנראה כנגד 5 אצבעות בכף-יד. כל ספרות המאיה נכתבות באמצעות שלושה סימנים פשוטים: נקודה - המסמנת את המספר אחד, קו - המסמל את המספר חמש, וקונכייה - המסמלת את המספר אפס. שיטה זו נחשבת למתקדמת למדי לתקופתה שכן כללה הן את השילוב של עיקרון תלות מיקום הספרה לסדר הגודל של המספר הנמצא בה והן את קיומו של המספר אפס שאף קדם למערכת המיקומית והיה לאלמנט מהפכני ביחס לתקופתו. בני המאיה היו הראשונים להכניס את האפס לשימוש מלא במערכת הספרות שלהם, שעה שבמערכות אחרות נהגו להותיר מקום ריק במקום בו אמור היה להופיע האפס.

בשיטת הספירה של המאיה, "גודלה האפקטיבי" של הספרה a (ספרה כלשהי) אשר נמצאה במקום $\ n$ המקיים $n\geq 3$ היה, לפי חישובי המאיה, $\ a\times 18\times 20^{n-2}$. כך, לדוגמה, ערכו של המספר ‏₂₀(8,14,3,1,12) היה:
$\ 12+1\times 20+3\times 18\times 20+14\times 18\times 20^{2}+8\times 18\times 20^{3}=1,253,912$.

אצל בני המאיה התקיים קשר הדוק בין שיטת הספירה ללוח השנה; אנשי המאיה עשו שימוש בשני לוחות שנה נפרדים: אחד בן 260 ימים אשר שימש לצרכים פולחניים וכלל 13 חודשים בני 20 יום כל אחד ואחד בן 365 ימים אשר שימש למטרות אזרחיות וכלל 18 חודשים בני 20 יום כל אחד ועוד "חודש" בין חמישה ימים.

המכנה המשותף הקטן ביותר של 260 ו-365 הוא 18,980 ימים, כלומר: 52 שנים אזרחיות או 73 שנים פולחניות, ואכן, לבני המאיה היה "מעגל ספירה" מקודש בן 52 שנים.

נוסף על לוח שנה זה, ספרו בני המאיה את הזמן מבריאת העולם, לפי אמונתם, בשנים בנות 365 ימים כל אחת. בכל שנה היו 18 חודשים בני 20 יום כל אחד, ועוד "חודש" קצר בן חמישה ימים שנחשב למביא מזל רע.

ככל הידוע, לא היו לבני המאיה שיטות לכפל ארוך ולא שימוש בשברים, אך למרות זאת הגיעו להישגים אסטרונומיים מרשימים. למשל, הם הצליחו לחשב את אורכה של השנה בתור 365.242 ימים כאשר כיום ידוע הערך של 365.242198 ימים.

העולם המוסלמי

בין המאה השמינית למאה החמש-עשרה לספירה חלו מספר התפתחויות חשובות במתמטיקה הערבית בכללותה ובאריתמטיקה בפרט.

בארצות ערב היו מקובלות שלוש שיטות ספירה עיקריות: השיטה האונארית, הבסיס הסקסגסימלי (שימוש במספר 60 כבסיס) והשיטה ההודית-ערבית. השיטה האונרית שימשה בעיקר לחישובי מסחר תוך שימוש באצבעות ככלי ספירה והייתה בשימוש בעיקר בקרב הסוחרים. המתמטיקאי הפרסי אבו אל-וואפה, שידע להשתמש גם בשיטה ההודית-ערבית, אמר עליה:

לא מצאתי לה שימוש בקרב חוגי אנשי העסקים והאוכלוסייה של הח'ליפות המזרחית במשך זמן רב.

השיטה הסקסגסימלית נכתבה בעזרת אותיות מהאלפבית הערבי והייתה בשימוש בעיקר לצורך חישובים אסטרונומיים. בקרב האסטרונומים המוסלמים היה השימוש בבסיס סקסגסימלי כה נפוץ עד כי כלליו זכו לכינוי "אריתמטיקה של אסטרונומים". השיטה העשרונית הובאה מהודו אך לא נעשה שימוש בסימנים מוסכמים בעת העבודה עמה כך שבמקומות שונים ניתן היה למצוא סימונים שונים. הערבים שכללו את השיטה ואת עיצוב הספרות והיו בעלי תרומה חשובה לעיצובו של המושג אפס.

"הספר התמציתי לחישוב על ידי השלמה ואיזון", ספרו של אבו ג'עפר מחמד אל ח'ואריזמי הנחשב לאבן דרך בהתפתחות האלגברה.

תקופת שלטונו של הח'ליף העבאסי החמישי הארון א-רשיד, השתרעה בין השנים 786-809, ומכונה לעיתים "תור הזהב העבאסי". תקופה זו לוותה בהתפתחויות חברתיות ותרבותיות רבות, בהן תרומות למתמטיקה. א-ראשיד עודד מחקר והתפתחות מתמטיים ובתקופתו תורגם ה"יסודות" לערבית. בתקופתו של בנו, הידוע בכינויו אל-מאמון, המשיכה פריחה זו. הוא הקים את בית החוכמה בבגדאד ובו אסף מלומדים רבים בני דתות שונות שעסקו במחקר ובתרגום של כתבים חשובים משפות זרות. במסגרת זו עמלו מתרגמים רבים בעלי השכלה מתמטית על תרגומם של כתבים מתמטיים חשובים, תוך מטרה להעשיר את הידע אשר היה ברשותם. בין מלומדים אלה נכלל ח'ואריזמי, אבי האלגברה. המילה "אלגברה" עצמה נגזרת משמו של אחד מספריו והמונח המתמטי "אלגוריתם" נגזר משיבוש שמו. להלן ציטוט מדבריו המדגים את גישתו:

אם אני תוהה ביני לביני בשאלה "במה בדרך כלל מעוניינים אנשים בחישוביהם?", אני מגלה כי כמעט תמיד זהו מספר.
מצאתי גם כי כל מספר מורכב מיחידות וכי כל מספר ניתן לפרק ליחידות. כמו כן, גיליתי כי כל מספר מאחד עד עשר גדול מקודמו ביחידה אחת. אחרי עשר, העשרות גדלות בכך שהן מוכפלות או משולשות כפי שהיו האחדות לפניהן וכך אנו מקבלים מספרים כמו עשרים ושלושים, כך עד מאה. כך, נתן להמשיך ולמנות את המספרים עד לגבול שממנו לא נוכל להעריכם יותר.

— אבו ג'עפר מחמד אל ח'ואריזמי

ביחס לתקופתו מבטאות מילים אלה הבנה עמוקה ומופשטת יחסית של המספרים. תרומתו החשובה של ח'וארזימי לפיתוח האלגברה הובילה לפתיחת כיווני מחשבה וכלים חדשים אשר איפשרו פיתוח נוסף ועמוק יותר של האריתמטיקה. נוסף על כך כתב ח'וארזימי מסה חשובה שעסקה בספרות ההינדיות. החיבור כולל את תיאור השיטה ומתייחס אף למספר אפס. ח'ואריזמי היה לחלוץ בפיתוחו של האפס בשילובו אותו במערכת הספירה מבוססת המקום. כמו כן, תיאר ח'וארזימי שיטות לביצוע חישובים אריתמטיים כגון מציאת שורש ריבועי. המתמטיקאי בן תקופתו אבו כאמל, הבין את החוק $\ x^{n}\cdot x^{m}=x^{m+n}$. המתמטיקאי הפרסי אל-קראג'י נחשב לאדם אשר ביסס את האלגברה סופית על בסיס הפעולות האריתמטיות (כפי שהיא מוכרת לנו כיום) ולא על בסיס הגאומטריה.

המספרים האי-רציונליים היו מוכרים לעולם המוסלמי; הפרסים עומר ח'יאם וכן נסיר א-דין א-טוסי טענו שכל יחס בין גדלים ניתן להציג כמספר, רציונלי או אי-רציונלי. עם זאת, לא אימצו הערבים את קיומם של מספרים שליליים. שברים עשרוניים הופיעו בספרות המתמטית האסלאמית כבר במאה העשירית.

ת'אבת אבן קורה, אחד מהמתמטיקאים שצמחו בבית החוכמה, ידוע בגילויה של משוואה המאפשרת למצוא זוגות של מספרים ידידותיים. המתמטיקאי אל-היית'ם פיתח את הידע בנושא המספרים המושלמים והעלה את המשפט הידוע כמשפט וילסון הטוען כי אם המספר p ראשוני אזי $1+(p-1)!$ מתחלק ב-p . לא ידוע האם הוכחת המשפט הייתה ידועה לו, אך הוכחה סופית למשפט זה ניתנה רק בשנת 1771 על ידי ז'וזף לואי לגראנז'. אל-פאריסי המשיך את המחקר בתחום המספרים הידידותיים. הוא נתן הוכחה חדשה למשפטו של אבן קורה תוך שימוש ברעיונות חדשים בנוגע לפירוק לגורמים וקומבינטוריקה. הוא מצא את זוג המספרים הידידים 17,296 ו-18,416.

האינקה

קיפו. ניתן להבחין בקשרים על החבלים

האינקה הייתה אימפריה שהתקיימה משנת 1200 בערך ועד כיבושה בשנת 1532. לתקופה קצרה בהיסטוריה שלטה אימפריית האינקה על שטח גדול באמריקה הדרומית, שכלל חלקים מהמדינות המודרניות פרו, בוליביה, אקוודור, צ'ילה וארגנטינה. באימפריה זו חיו כ-6 מיליון איש בני עמים שונים, שדיברו ביותר מ-700 שפות.

באימפריית האינקה לא נעשה שימוש בכתב ולכן הדבר מקשה את הבנתנו לגבי הרמה המתמטית אליה הגיעו בני תרבות האינקה. החוקר G. Urton טוען בספרו כי לאינקה הייתה רמה מתמטית אשר כללה הבנה מופשטת של המספרים.

למרות היעדר הכתב, ניהולה של מערכת מדינית כה גדולה דרש צורה מסוימת של אחסון מידע מתמטי (כגון מסים, כלי נשק, בהמות וכו'). לצורך אחסון המידע המתמטי השתמשו האינקה בכלי הנקרא קִיפּו, מילולית: קשר. הקיפו היה עשוי חבלים כך שאחסון המידע עליו התבצע באמצעות קשירות עם מערכת מיקום עשרונית כך שגודלה המוחלט של ספרה בוטא על ידי מספר קשרים רצופים. לדוגמה: שלושה קשרים רצופים בתחילת החבל ייצגו שלושה אחדות, חמישה קשרים רצופים המופיעים אחריהם ייצגו חמש עשרות וכו'. אפס בוטא על ידי השארת מרווח גדול בין הקשרים. כיוון שבקיפו נכרכו יחדיו מספר חבלים, הבידול ביניהם (כך שניתן יהיה לזכור איזה חבל מיצג איזה מספר) נעשה על ידי קשירת חבלים בצבעים שונים. דרך נוספת לבידול החבלים הייתה על ידי יצירת "חבלי משנה" אשר חוברו ל"חבל ראשי" באמצעו.

מלך האינקה מינה פקידים אחראי קיפו אשר היו קרויים "קויפוקאמאיוק". אלה הוצבו בכל עיר וערכו רישומים שונים כאשר בערים גדולות היו מספר פקידים. הקיפו היו בשימוש גם בידי מערכת המשפט. ידוע על מכשיר בשם יוּפּנה אשר שימש את האינקה כמעין חשבונייה. ישנן מספר השערות לגביו, לגבי תפקידו ואופן פעולתו.

האריתמטיקה ביהדות

האריתמטיקה במקרא

מתקופת המקרא בני ישראל עשו שימוש במתמטיקה ובאריתמטיקה לצרכים שונים, בין היתר בעקבות הצורך בה בהלכה, כגון חוקי השבת האוסרים ללכת בשבת למעלה מתחום השבת, חוק הכלאים שלפיו אסור לזרוע שני מיני זרעים יחד אלא במרווח מסוים, ניתוחים אסטרונומיים לצורך חישובים הנוגעים ללוח העברי לצורכי קביעת המועדים ועוד.

העברים השתמשו בגרסה של שיטה העשרונית שהייתה בנויה על חוקי החיבור והכפל, ולמרות זאת אנו יודעים כי חלק מן המידות והמשקולות במקרא נמדדו על פי בסיס 60 ובסיס 12. אף שייתכן כי לבני ישראל הייתה, כמו לשאר עמי הסהר הפורה הקדום, ובהם הבבלים והמצרים, שיטת ספירה משלהם, התנ"ך איננו כולל סימנים אריתמטיים, והמספרים כתובים בו אך ורק במילים. כל מספר מ-1 עד 10 נקרא בתנ"ך בשם שונה. שמות המספרים מ-11 עד 19 בנויים מצירוף היחידות אל העשרת, כבעקרון החיבור. השם "עשרים" הוא צורת רבים זוגית של המילה עשר, והוא מורה על פעולת הכפל "עשר כפול שתיים". באותו האופן, גם המילה "שלושים" היא בעצם "שלוש כפול עשר", כאשר סיומת הרבים "-ים" מהווה בהקשר זה, הלכה למעשה, סימן לשוני לכפל בעשרת.

היחידה הראשונה אחרי עשר היא מאה, אחריה אלף, והשלישית והגדולה ביותר במקרא היא רבבה, וברבים רבבות או ריבוא.

מספרים עבריים במילים:

המספר:	10,000	1,000	100	20	11	10	9	8	7	6	5	4	3	2	1
המילה:	רבבה	אלף	מאה	עשרים	אחת-עשרה	עשר	תשע	שמונה	שבע	שש	חמש	ארבע	שלוש	שתיים	אחת

כתיבת מספרים גדולים במקרא התבצעה בשתי דרכים שונות. האחת היא "בסדר עולה", כלומר – מהיחידה הקטנה ביותר אל היחידה הגדולה ביותר. דוגמה: "ויחי ירד שתים ושישים שנה ומאת שנה, ויולד את חנוך" (ספר בראשית, פרק ה', פסוק י"ח). דרך זו היא הקדומה יותר והיא נובעת, ככל הנראה, מקשיי התפיסה של האדם הקדמון באשר לכמות, קרי: היה לו קל יותר לספור ראשית את היחידות – איתן התעסק רבות והכיר היטב – ובשלב הבא לעסוק במספרים בסדרי גודל היותר "מרוחקים" ממנו ושהיכרותו עמם מעורפלת יותר.

הדרך השנייה לכתיבת מספרים היא לפי "סדר יורד", כלומר – מן היחידה הגדולה ביותר לקטנה ביותר. בכל ספרי הנביאים פרט ליחזקאל, כתובים המספרים בסדר יורד. דוגמה: "ויהי משקל הזהב, אשר בא לשלמה בשנה אחת, שש מאות ושישים כיכר זהב" (ספר מלכים א', פרק י', פסוק י"ד).

במקביל, ישנם מקומות שבהם שתי הדרכים הנ"ל "מתערבבות", כלומר, חלק אחד במשפט נכתב בסדר עולה, והשני בסדר יורד. דוגמה: "ויהי כל בכור זכר במספר שמות, מבן חדש ומעלה לפקודיהם, שנים ועשרים אלף, שלושה ושבעים ומאתיים" (ספר במדבר, פרק ג', פסוק מ"ג).

השימוש באריתמטיקה בקרב בני ישראל היה רב, שכן זו היוותה כלי חשוב למתן תרומות ומעשרות, מיקח וממכר, הן עם ישראלים והן עם עמי האזור, גביית מס מארצות כבושות ועוד. איננו יודעים בוודאות כיצד ערכו העברים את חישוביהם, אך הסברה ההגיונית ביותר היא שבנוסף לעשר אצבעותיהם נעזרו באבקוס כמו המצרים והבבלים.

ישנם בתנ"ך תרגילי חשבון הערוכים במלואם, לדוגמה: "אולי יחסרון חמישים הצדיקים חמישה, התשחית בחמישה את כל העיר? ויאמר: לא אשחית אם אמצא שם ארבעים וחמישה" (ספר בראשית, פרק י"ח, פסוק כ"ח), כלומר 45=50-5.

במקביל אליהם, מופיעים בתנ"ך אף תרגילי חשבון חלקיים. למשל, ישנם בתנ"ך מופעים בהם החסירו את אחד הגורמים, כמו: "וכי יגף שור איש את שור רעהו ומת, ומכרו את השור החי וחצו את כספו" (שמות כא לה). ישנם גם פעמים בהם נתונים הגורמים, אך התוצאה חסרה, כמו: "ראה זה מצאתי, אמרה קהלת, אחת לאחת למצוא חשבון" (מגילת קהלת, פרק ז', פסוק כ"ז) ובלשון מתמטית: ?=1+1.

היחס אל האריתמטיקה כפי שמופיע בתורה ובכתבים מאוחרים יותר, הוא ברובו כאל כלי שימושי ולא כאל מדע מחקרי. ככל הנראה, קיבלו בני ישראל את מרבית ידיעותיהם האריתמטיות מהעמים הסובבים אותם.

השברים במקרא

במקרא מצויים שברים רבים והם: חצי, רבע, חמישית, שישית ועשירית. יש להניח שהשברים 1/20, 1/30 ו- 1/50 נכנסו לחישוביהם של העברים, מכיוון שהגרה הייתה החלק העשרים של השקל, הסאה – החלק השלושים של החומר והשקל – החלק החמישים של המנה.

העבריים, כמו המצרים באותה התקופה, לא השתמשו בשברים שאינם שברים יסודיים (בעלי מונה הגדול מאחד), זאת אנו למדים מאי הופעתם של שברים שאינם יסודיים במקרא. סביר להניח שזאת משום שלא הבינו את מושג השבר שמונהו גדול מ-1. השברים שמונהם גדול מאחד מצוינים במקרא על ידי המילה "ידות" המצינת ריבוי של שברים שמונהם אחד. לדוגמה:

ונתתם חמישית לפרעה, וארבע הידות יהיה לכם

— ספר בראשית, פרק מ"ז, פסוק כ"ד

"ארבע הידות", משמעו, "ארבעה חלקים". המחקר המודרני מחזק השערה בדבר אי הכרת שברים שאינם יסודיים בטיעון כי אדם מודרני היה כותב "חמישית...והשאר", או את המונה והמכנה, כפי המקובל כיום: "ונתתם חמישית לפרעה, וארבע החמישיות יהיה לכם".

איזכור ה"עשרון" בתנ"ך — "שלושה עשרונים לפר ושני עשרונים לאיל" (ספר במדבר, פרק כ"ח, פסוק כ') — איננו סותר הנחה זו, משום שהעשרון הווה יחידת מידה, ואף נקרא לעיתים בשם אחר, הלא הוא עומר: "וְהָעֹמֶר עֲשִׂרִית הָאֵיפָה הוּא" (ספר שמות, פרק ט"ז, פסוק ל"ו). בכל הנוגע למספרים מעורבים, העברים נהגו לכתוב את השלם לפני השבר. דוגמה: "ועשו ארון עצי שטים, אמתיים וחצי אורכו, אמה וחצי רוחבו, ואמה וחצי קומתו" (ספר שמות, פרק כ"ה, פסוק י').

אריתמטיקה עברית בימי הביניים

גם במקורות היהודיים נכתבו במשך הדורות קירובים שונים ל-2√ (שערכו המקורב הוא ...1.41421). במסכת אהלות נכתב הקירוב 4/3, שהוא 1.333. במסכת עירובין נ"ז ע"א נכתב: "כל אמתא בריבוע (ריבוע של 1X1), אמתא ותרי חומשי באלכסונא". כלומר, הערך המקורב בקטע זה הוא 7/5 שהוא 1.4. קירוב נוסף (106/75) מופיע בצורה עקיפה בתלמוד הירושלמי. בפירושו למסכת עירובין כותב הרמב"ם: שטח מרובע שיהיה עומד הזווית יהיה מידתו ה' אלפים אמה, לא יִוָדַע צלע אותו שטח, אלא בקרוב, לפי שה' אלפים הוא חשבון בלתי גדור וגדרו בקרוב שבעים אמה וה' שבעיות אמה. והדבר בכאן בזה החשבון כמו שזכרתי לך במה שקדם בייחוס אלכסון עגולה למסבבה. כי לא יגיע לעולם לידיעת גדר החשבון, שאינו גדור אלא בקירוב, ואין זה לחסרון דעתנו אלא מפני טבע זה החשבון. כלומר הרמב"ם מבטא את ההשערה כי השורש הריבועי של 2 איננו ניתן ל"גידור", כלומר להגדיר באמצעות שבר, אלא רק לקירוב, שכן הוא מספר אי-רציונלי. עוד הוא טען כי תופעה זו היא מעצם טבעו של החשבון, ולא טעות אנוש.

החיבור העברי "משנת המידות" נחשב לספר המתמטיקה העברי הראשון. ציטוטים ממנו משוקעים בדברי חכמי היהודים מימי הביניים, אולם במאה ה-19 התגלה לראשונה קטע כתב יד של החיבור בעצמו, מאז ועד היום נמצאו עוד שני קטעי כתב יד, היוצרים יחדיו את החיבור השלם, המכיל 6 פרקים ו-49 משניות, כאשר כתב היד המוקדם ביותר מתוארך למאה ה-12 לספירה. על זהות המחבר וזמנו חלוקות הדעות, יש המתארכים אותו לראשית התקופה המוסלמית, המאה ה-9 לספירה, ויש המקדימים ומייחסים אותו לתנא רבי נחמיה, בן המאה ה-2 לספירה.

במאה האחת עשרה ובמאה השתים עשרה פורסמו מספר כתבים חשובים בנושא האריתמטיקה על ידי אברהם בר חייא (ראב"ח) ואברהם אבן-עזרא אשר סימנו את "לידתה" של המתמטיקה העברית. בר-חייא, יליד ברצלונה, אשר נחשב לאבי המדע העברי, חיבר אנציקלופדיה מדעית וחיבורים מתמטיים רבים, בהם "יסודי התבונה ומגדל האמונה" ו"חיבור המשיחה והתשבורת" השופכים אור על המחשבה המתמטית שהונהגה באותה תקופה בארצות האסלאם המערביות. בספר זה מופיע איזכור עברי ראשון לפונקציות הטריגונומטריות.

חיבורו של אבן עזרא, יליד אראגון, "ספר המספר", פרש לראשונה את הצגתה של מערכת ספירה עשרונית תלוית-מיקום הכוללת את האפס. בספר זה מוסברים עקרונות אריתמטיים חשובים כגון ארבע פעולות חשבון, שברים, פרופורציות ושורשים ריבועיים. הרמב"ם פיתח שיטה מתמטית לחישוב מופעי הירח.

המאה הארבע עשרה אופיינה בתנופת תרגום בה תורגמו יצירות חשובות לעברית, הכוללות בין היתר כתבים מרכזיים של תלמי, אוקלידס (ובכלל זה ספרו המפורסם "יסודות") ואבו איבן אל חיתאם. פרסום יצירות אלה הכשיר את הקרקע לכתיבת יצירות מקור עבריות. בתקופה זו פרסם המלומד היהודי מטולדו יהודה בן סלומון הכהן, ראשית בערבית, אנציקלופדיה מדעית בשם "מדרש החוכמה". חיבור מתמטי בעל נדבך אריתמטי מעניין מאד מתקופה זו הוא "ספר המלכים" העוסק בתכונותיהם של מספרים טבעיים. לוי בן גרשום חיבר מספר כתבים בנושאים מדעיים, בהם אריתמטיקה. מספר שנים אחר כך עסק עמנואל בין יעקב בהצגתם של שברים עשרוניים ובתכונות המעגל.

המאה החמש-עשרה מאופיינת בהעברת עיקר "מרכז הכובד" המחקרי לאיטליה, שם המשיך תרגומן של יצירות חשובות. בין הבולטים מבין העוסקים במלאכה, ניתן למנות את מרדכי פינזי אשר תרגם את ספרו של אבו כאמל, "אלגברה", וחיבר את היצירה החשובה, "מאמר בחשבון מדידות הגיגיות והחביות".

מבין יהודי האימפריה הביזנטית בולטת במיוחד עבודתם של אברהם קומטינו, מחבר "ספר החשבון והמידות", של אליהו מזרחי, מחבר "ספר המספר" ושל כלב אפנדופולו אשר תרגם את ספרו של ניקומכוס "מבוא לאריתמטיקה" לעברית.

גימטריה

ערך מורחב – גימטריה

גימטריה, מתן פרשנות למילה או למחרוזת מילים לפי סכום ערכן המספרי של האותיות, נפוצה מאד בהלכה ובתורת הקבלה. כמו הרומים והיוונים, השתמשו חכמי התלמוד בעשרים ושתים אותיות האלפבית העברי לסימון מספרים.

הגימטריה משמשת כדרך לקבלת רמז להבנת הכתוב וככלי פרשני שולי נמצאה בשימוש התנאים והאמוראים במדרש, אך אין לומדים הלכות מגימטריה (אלא אם כן הן מקובלות במסורת כהלכה למשה מסיני). בברייתא של רבי אליעזר הגלילי היא נמנית עם המידות שהתורה נדרשת בהן באגדה.

בפרקי אבות, לעומת זאת, מודגש ערכה השולי של הגימטריה:

ר' אלעזר חסמא אומר: קינין ופתחי נידה הן גופי הלכות, תקופות וגימטריאות - פרפראות לחכמה.

— משנה, מסכת אבות, פרק ג', משנה י"ח

אותיות האלפבית העברי משמשות לכתיבת ספרות עבריות, לפי ערכן המספרי של האותיות המופיע בטבלה:

משמעות אותיות האלפבית העברי בגימטריה:

האות:	ת		ש		ר		ק		צ		פ		ע		ס		נ		מ		ל		כ		י		ט		ח		ז		ו		ה		ד		ג		ב		א
המספר:	400		300		200		100		90		80		70		60		50		40		30		20		10		9		8		7		6		5		4		3		2		1

לעיתים נמצא בהלכה ערכים נפרדים לאותיות מנצפ"ך, כך שמתקיים: ך=500 ,ם=600 ,ן=700, ף=800 ,ץ=900.

אירופה מימי הביניים ועד לתום תקופת הרנסאנס

אנדרטה שהוקמה לזכרו של לאונרדו מפיזה

לאחר שקיעתה של תרבות יוון העתיקה, התפתחות האריתמטיקה בפרט והמתמטיקה בכלל באירופה נעצרה כליל. הסיבה לכך הייתה התפשטות הכנסייה הקתולית ברוב אזורי אירופה. ההתפתחות המדעית קפאה על שמריה, שכן בימי הביניים רובם המוחלט של האנשים המשכילים היו אנשי הכנסייה שדגלה בכפיית "משטר מחשבתי". ומשום שלא נערכו מחקרים מדעיים, לא היה צורך במתמטיקה לשם חישובים מורכבים. לכן, התעניינו אנשי אירופה של ימי הביניים באריתמטיקה לצורך חישובים יומיומיים בלבד, כגון מחירי סחורות, תרומות לכנסייה וכו'.

רוב ההתפתחות המתמטית באותה תקופה הייתה בעולם המוסלמי, בהודו ובסין. הערבים שילבו את המתמטיקה של היוונים, שהתבססה ברובה על עקרונות גאומטריים עם המתמטיקה ההודית שהתבססה ברובה על עקרונות אלגבריים, באותה התקופה, ואף הגיעו בעצמם להישגים ניכרים. השפעת המדענים המוסלמים על מדעני ספרד היהודים הייתה גדולה ומכרעת. האדם שהעביר את השיטה העשרונית ממקורות יהודים או ישירות מהמתמטיקה הערבית למתמטיקה הלטינית-נוצרית במערב אירופה היה המתמטיקאי הנוצרי לאונרדו מפיזה, הידוע גם בשם "פיבונאצ'י". ספרו "ספר החשבונייה" היה הראשון באירופה, מלבד ספרד, בה הוצגה השיטה העשרונית. הלכה למעשה, היווה ספר זה סיכום של כל הידע האריתמטי המרכזי עד לאותה התקופה. מושג האפס גם הוא יובא על ידי פיבונאצ'י, ונראה לראשונה במערב באחד מספריו.

בתקופת הרנסאנס החלה תחייה של המדעים והאומנויות באירופה. כחלק מההתחדשויות המדעיות, החלה לעלות בשנית קרנה של המתמטיקה, שהפכה שוב לגוף ידע נצרך. הדבר הוביל להתעניינות מחודשת אף באריתמטיקה, ואנשי התקופה המשיכו בחקר אריתמטי ושיפור, סיכום ופיתוח הידע שנצבר לפניהם.

העת החדשה

דף מתוך מאמרו של לייבניץ העוסק במספרים בינאריים

כריכת ספרו החשוב של גאוס "Disquisitiones Arithmeticae"

בהאצת מהפכת הדפוס, התקיים תהליך של האחדה בינלאומית בסימונים ובשיטות האריתמטיות והתקבעה מערכת אריתמטית תקנית הכוללת כתיבה בספרות הודיות, שימוש בבסיס העשרוני לצורכי חישוב יום-יומיים ולרוב הכתיבה המדעית והטכנולוגית ומערכת מוסכמת של סימונים שונים לצורכי הכתיבה האריתמטית. בד בבד לשימוש במערכת זו, נכנסו לשימוש מערכות כתיבה נוספות המשמשות בעיקר בתחומי המדע והטכנולוגיה, כגון הבסיס הבינארי וההקסדצימלי. הבסיס הבינארי, בו ישנן שתי ספרות - 0 ו- 1, פותח על ידי לייבניץ במאה ה-17 ונכנס לשימוש רב בעת החדשה בעיקר במערכות אלקטרוניקה ספרתית ובמחשבים, שם הוא משמש כחלק משפת המכונה.

ההתפתחות המתמטית בעת המודרנית הרחיבה את מושג ה"אריתמטיקה" באופן שהוא איננו עוסק עוד אך ורק בפעולות חישוב אלמנטריות, אלא כולל גם תחומים משיקים או קרובים, כך שגבולותיו כיום אינם מוגדרים לחלוטין. המינוח "אריתמטיקה", בראי מודרני, יכול להתייחס אף לתחומים כגון תורת המספרים, גאומטריה אלגברית ותחומים נוספים.

מגאוס ואילך - אריתמטיקה בראי מודרני

בשנת 1801 פרסם המתמטיקאי קארל פרידריך גאוס את ספרו Disquisitiones Arithmeticae (בעברית: "מחקרים אריתמטיים") בו דן בנושאים מרכזיים באריתמטיקה, בין היתר דן בספרו בבעיות של משוואות ריבועיות ובנייה בסרגל ומחוגה עליהן אמר:

התאוריה של חלוקת המעגל בפני עצמה ... איננה שייכת לתחום האריתמטיקה, אך עקרונותיה משליכים על אריתמטיקה גבוהה.

אותם עקרונות המתמטיקה הגבוהה שבהם דן גאוס בספרו היוו מקור להתעניינותם של מתמטיקאים נוספים אשר שאפו בחלקם לבסס את יסודותיהם של ענפים שונים במתמטיקה, בעיקר האנליזה, על מצע של אריתמטיקה איתנה. מתמטיקאים כדוגמת ארנסט קומר, לאופולד קרונקר, ויליאם ווטרהאוס ואחרים העמיקו, חקרו וביססו את האריתמטיקה המודרנית. על כך אמר המתמטיקאי דויד הילברט כי המתמטיקה של המאה התשע-עשרה התפתחה "בסימן המספרים". המתמטיקאי הגרמני פליקס קליין השתמש במינוח "אריתמטיזציה של המתמטיקה". קרונקר ודיריכלה טענו כי בסופו של יום, כל טענה באלגברה או באנליזה מבוססת על תכונותיהם של המספרים הטבעיים.

צעד חשוב נוסף לקראת ביסוס האנליזה המודרנית על בסיס אריתמטי איתן ניתן בעבודותיהם של גיאורג קנטור, אוגוסטן לואי קושי וריכרד דדקינד, שהציגו מבט חדשני על מהותם של מספרים. אחת הדוגמאות להתקדמות שכזו היא פיתוחם של חתכי דדקינד. כמו כן, בוצעה התקדמות בעיצובם של אובייקטים מתמטיים כגון סדרות. משפטים והגדרות רבים בחשבון דיפרנציאלי ואינטגרלי, למשל, ניתנים להצגה על ידי מאפייניהן של סדרות.

עבודתו המקיפה של שארל הרמיט, בהשראת כתביו של גאוס, לגראנז' ושל יעקבי הרימה אף היא תרומה משמעותית לפיתוח האריתמטיקה המודרנית ולתחומים המשיקים לה. המתמטיקאי הרוסי איגור זולוטרב תרם תרומה נוספת להבנתם של המספרים האלגבריים.

הרמן מינקובסקי פיתח את "גאומטריית המספרים" שהיא ענף חשוב באריתמטיקה המודרנית.

התפתחות סימני הפעולות

במקביל להתפתחות מערכות הספירה וסימני הספרות, גם סימוני הפעולות עברו התפתחות ארוכה במרוצת השנים, עד להתקבעות הסימונים המוסכמים כפי שהם מוכרים כיום. בתחילת דרכה של האריתמטיקה יוצגו רוב הבעיות מילולית ולא בעזרת סימנים מתמטיים מיוחדים. סימנים לחיבור וחיסור הונהגו כבר במצרים העתיקה, בעיקר כחלק משיטת הכתיבה השברית בה נהגו המצרים הקדמונים. הראשון להכניס סימוני פעולות מוסכמים לשימוש נרחב יותר היה דיופנטוס, שהכניס סימונים מקוצרים בדמות אותיות לציון פעולת החזקה כאשר חיסור בוטא על ידי הסימן ψ וחיבור על ידי כתיבת המספרים זה לצד זה.

ההודים נהגו לסמן חיסור על ידי נקודה מעל המחוסר וכפל על ידי קיצור המילה המתאימה בהודית. שברים סומנו על ידי כתיבת המכנה מתחת למונה ללא קו שבר. חזקות שונות יוחסו לצבעים שונים כך שסימון החזקה בוצע על ידי קיצורי מילים של שם הצבע.

לוקה פאצ'ולי השתמש באות p (האות הראשונה של המילה plus) כדי לסמן את פעולת החיבור, באות m (האות הראשונה של המילה minus) כדי לסמן חיסור, בסימן co (האותיות הראשונות של המילה cosa שמשמעה "משהו") כדי לסמן נעלם, בסימן ce כדי לסמן נעלם בריבוע, cu על מנת לסמן נעלם בשלישית, ae (קיצור של aequalis, שוויון) על מנת לסמן שוויון ובאות r (האות הראשונה של radix) על מנת לסמן שורש ריבועי, סימן שהתפתח לבסוף לסימון המוכר "√".

סימן האחוז התפתח בהדרגה מקיצור המילה "per cento" שמשמעותה "למאה" לאות p. הסימון המשיך להתפתח ובסביבות השנה 1650 הופיע כבר בתור הסימן "${\frac {\circ }{\circ }}$". עם השנים, הוטה הקו ונהפך לסימן המוכר כיום: "%".

ישנה מחלוקת לגבי מקור הסימונים המודרניים המשמשים לחיבור וחיסור. ההשערה המקובלת בנוגע לסימן החיבור היא כי התפתח כקיצור למילה הלטינית "et" שמשמעותה "וגם" כאשר נכתבו הבעיות בצורה מילולית, בדומה להתפתחות הליגטורה "&". בנוגע לסימן החיסור, השערה אחת היא כי התפתח מאחד הסימנים אשר שימשו בכתיבה האיטלקית כסימונים מקוצרים לפעולת החיסור: ${\tilde {m}}$ או ${\bar {m}}$, אולי אף מהאות m עצמה. השערה נוספת היא כי הסימון התפתח מהסימון ההודי של נקודה מעל המחוסר.

רוברט רקורד הכניס לשימוש את סימונם של שני קווים אופקיים מקבילים באורך זהה בתור סימן השוויון כאשר כסיבה לכך כתב:

מפני שאין שני דברים שיכולים להיות יותר שווים זה לזה.

המתמטיקאי האנגלי תומאס האריוט הכניס לשימוש את הסימונים >, < ו- $\cdot$ (עבור כפל), את האחרון בהשפעתו של כריסטופר קלאוויוס. ויליאם אאוטרד הכניס את השימוש בסימן × עבור כפל, כאשר כיום שניהם נמצאים בשימוש. כמו כן שמורה לאאוטרד הזכות על הכנסת השימוש בסימנים "≠" לציון אי-שוויון ו-"::" לציון פרופורציה. רנה דקארט הכניס לשימוש את סימון החזקה המודרני.

ראו גם

• אריתמטיקה
• היסטוריה של המדע
• היסטוריה של המתמטיקה
• פילוסופיה של המתמטיקה
• שיטות ספירה
• אפס של פונקציה

לקריאה נוספת

• אוסף מקורות לקורס "תולדות המתמטיקה", בהוצאת המכללה לחינוך על שם קיי בבאר שבע
• האנציקלופדיה העברית, הערכים אריתמטיקה ומתמטיקה
• רחל רוזנבוים, חכמת התשבורת: המתמטיקה באספקלריה יהודית, ירושלים: מוסד הרב קוק, תשס"ג 2003
• גד בן-עמי צרפתי, מונחי המתמטיקה המדעית העברית של ימי הביניים, ירושלים: י"ל מאגנס, תשכ"ט 1968
• שמעון דגן (בעריכת ד"ר דב ירדן), תולדות המתמטיקה הקדומה, הוצאת דביר, 1955
• שבתאי אונגורו, ‏מבוא לתולדות המתמטיקה, סדרת אוניברסיטה משודרת, בהוצאת משרד הביטחון – ההוצאה לאור, 1989
• בנו ארבל, קיצור תולדות המתמטיקה, מכון מופ"ת, 2005
• שמעון דגון, תולדות המתמטיקה הקדומה, הוצאת דביר, תשס"ז

• The shaping of arithmetic: after C.F. Gauss's Disquisitiones Arithmeticae, Catherine Goldstein, Norbert Schappacher, Joachim Schwermer, editors. Berlin New York: Springer, 2007
• Encyclopaedia of the history of science, technology, and medicine in non-western cultures, editor: Helaine Selinm, Dordrecht, The Netherlands: Kluwer Academic, c1997

קישורים חיצוניים

• The MacTutor History of Mathematics archive
• Harry Foundalis, Greek Numbers and Numerals (Ancient and Modern)
• Douglas Weaver with the assistance of Anthony D. Smith, The History of Mathematical Symbols
• Earliest Uses of Various Mathematical Symbols