e (קבוע מתמטי)

בערך זה |
e (נקרא גם קבוע אוילר על שם לאונרד אוילר, או קבוע נפייר על שם ג'ון נפייר) הוא קבוע מתמטי טרנסצנדנטי חשוב שערכו בקירוב 2.71828182845904, המשמש כבסיס הלוגריתם הטבעי.
ניתן להגדיר את הקבוע e בדרכים אחדות, השקולות זו לזו. הקבוע e מתאר את הגידול בסוף השנה בהפקדת סכום כסף בריבית של 100% לשנה, לו היה הבנק מחשב את סכומי הריבית המגיעים למפקיד בכל רגע ומפקיד אותם מיד באותם תנאים. באופן זה e מוגדר כגבול הערך $ \left(1+{\frac {1}{n}}\right)^{n} $ כאשר $ n $ שואף לאינסוף. מכיוון שתהליכים בטבע מצייתים לחוקי התנהגות רגעיים, הקבוע מופיע כמו מעצמו בתיאור של תופעות רבות בהן קיים שינוי רציף, כמו גם בחישובי ריבית.
הסימון באות מיוחדת עבור e הוכנס לשימוש על ידי לאונרד אוילר ב-1727.
היסטוריה
האזכור הראשון לקבוע זה פורסם ב-1618 בטבלה בסוף עבודה על לוגריתמים מאת ג'ון נפייר. אולם, הטבלה לא כללה את המספר עצמו אלא רק רשימת לוגריתמים שחושבו על פי הקבוע. ההנחה הרווחת היא שהטבלה נכתבה על ידי ויליאם אוטרד. ההתייחסות הראשונה למספר בתור קבוע הייתה של יאקוב ברנולי, כשניסה למצוא את הערך של הביטוי: $ {\displaystyle \lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}} $ השימוש הראשון לקבוע, שסומן אז בתור b, הוא במכתב ששלח גוטפריד לייבניץ אל כריסטיאן הויגנס ב-1690. לאונרד אוילר סימן לראשונה את הקבוע כ-e ב-1727, והפרסום הראשון שעשה שימוש בסימון זה היה ספרו של אוילר "מכניקה"(אנ') מ-1736. אף על פי שבשנים הראשונות חלק מן החוקרים השתמשו באות c, האות e הייתה נפוצה יותר ולבסוף הפכה לסטנדרט המדעי.
הסיבה לשימוש דווקא באות זו אינה ידועה, אבל סביר שזה בגלל היותה האות הראשונה במילה הלטינית אקספוננט. אפשרות נוספת היא שאוילר בחר אות זו היא, כי זוהי התנועה הראשונה אחרי האות a, שכבר הייתה בשימוש. לא ברור, על פי אפשרות זו, למה אוילר בחר דווקא תנועות ולא עיצורים. אפשרות נוספת היא שאוילר בחר באות זאת כי זאת האות הראשונה בשם משפחתו (euler).
הגדרה

e מוגדר כך שהשטח הצבוע בתכלת שווה ל-1
מקובלות ארבע דרכים להגדרתו המתמטית של המספר e, כולן שקולות:
1. הגבול של הסדרה הבאה: $ {\displaystyle e=\lim _{n\to \infty }\left(1+{1 \over n}\right)^{n}} $
הגדרה זו למעשה מתארת 'גידול המשכי', המופיע הן בחישובי ריבית דריבית והן בגדילה וצמיחה בעולם החי, בו התאים משכפלים את עצמם והצמיחה היא בקצב אחיד לאורך תקופות. על כך בהרחבה בהמשך.
2. מהגדרה זו נובע שעד כדי כפל בקבוע, הפונקציה $ e^{x} $ היא היחידה השווה לנגזרת של עצמה ולכן e הוא היחס $ y(1)/y(0) $ כאשר $ y(x) $ היא פונקציה המקיימת את המשוואה הדיפרנציאלית $ y'(x)=y(x) $ ואיננה זהותית 0.
3. פיתוח עובדה זו לטור טיילור (או חישוב הגבול באינסוף של הסדרה הנ"ל בעזרת הבינום של ניוטון) מספק טור אינסופי המסתכם ל-$ \sum _{n=0}^{\infty }{\frac {1}{n!}}={\frac {1}{0!}}+{\frac {1}{1!}}+{\frac {1}{2!}}+\dots =e $.
4. המספר $ \,x $ המקיים: $ {\displaystyle \int _{1}^{x}{\frac {1}{t}}\,\mathrm {d} t={1}} $
- כלומר, e הוא המספר $ \,x $ שעבורו השטח שמתחת להיפרבולה $ \,f(t)=1/t $ מ-1 ועד $ \,x $ שווה ל-1.
דרכים נוספות לחישוב e
| סכום טור אינסופי | |
$ e=\left[\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{k!}}\right]^{-1} $
| |
$ e=\left[\sum _{k=0}^{\infty }{\frac {1-2k}{(2k)!}}\right]^{-1} $
| |
$ e={\frac {1}{2}}\sum _{k=0}^{\infty }{\frac {k+1}{k!}} $
| |
$ e=2\sum _{k=0}^{\infty }{\frac {k+1}{(2k+1)!}} $
| |
$ e=\sum _{k=0}^{\infty }{\frac {3-4k^{2}}{(2k+1)!}} $
| |
$ e=\sum _{k=0}^{\infty }{\frac {3k^{2}+1}{(3k)!}} $
| |
$ e=\left[\sum _{k=0}^{\infty }{\frac {4k+3}{2^{2k+1}\,(2k+1)!}}\right]^{2} $
| |
$ e={\cfrac {-12}{\pi ^{2}}}\left[\sum _{k=1}^{\infty }{\cfrac {1}{k^{2}}}\ \cos \left({\cfrac {9}{k\pi +{\sqrt {k^{2}\pi ^{2}-9}}}}\right)\right]^{-1/3} $
| |
$ e=\sum _{k=1}^{\infty }{\frac {k^{2}}{2(k!)}} $
| |
| שבר משולב אינסופי | $ e=2+{\cfrac {1}{1+{\cfrac {1}{2+{\cfrac {2}{3+{\cfrac {3}{4+{\cfrac {4}{5+_{\ddots }}}}}}}}}}} $
|
| גבול | $ e=\lim _{n\to \infty }n\cdot \left({\frac {\sqrt {2\pi n}}{n!}}\right)^{1/n} $
|
$ e=\lim _{n\to \infty }{\frac {n}{\sqrt[{n}]{n!}}} $
| |
$ e=\lim _{x\to \infty }{\biggl (}1+{\frac {1}{x}}{\biggr )}^{x} $
| |
$ e=\lim _{x\to -\infty }{\biggl (}1+{\frac {1}{x}}{\biggr )}^{x} $
| |
$ e=\lim _{x\to 0}{\sqrt[{x}]{1+x}} $
| |
| מקסימום | $ e=\max {\sqrt[{x}]{x}} $
|
תכונות
 ערך מורחב – טרנסצנדנטיות של e
ערך מורחב – טרנסצנדנטיות של e
e הוא מספר אי-רציונלי. יתרה מכך, הוא גם מספר טרנסצנדנטי, כלומר – e אינו שורש של פולינום בעל מקדמים רציונליים.
לפונקציה המעריכית $ \!\,e^{x} $ (אקספוננט) יש תכונה מיוחדת: הנגזרת שלה שווה לפונקציה עצמה. כלומר: $ \!\,(e^{x})'=e^{x} $. תכונה זו ייחודית לפונקציית האקספוננט (ולכפולות שלה בקבועים). את פונקציית האקספוננט נהוג לרשום גם כ-$ \ \exp(x) $ ואז $ \,\exp(1)=e $. רישום זה נפוץ בספרים ישנים, שבהם היה קושי להציג נוסחאות מורכבות בגלל מגבלות ההדפסה.
הפונקציה ההפוכה לפונקציית האקספוננט היא פונקציית הלוגריתם הטבעי $ \!\,\log _{e}x $, המסומנת בקיצור כ-$ \!\,\ln x $.
הפונקציה $ \ e^{x} $ גם משמשת להגדרת הפונקציות הטריגונומטריות (סינוס וקוסינוס) כאשר הארגומנט הוא מספר מדומה, באמצעות נוסחת אוילר:
- $ \ e^{i\theta }=\cos \theta +i\sin \theta =cis\theta $
כאשר נציב בנוסחה זו $ \ \theta =\pi $ נקבל את הקשר בין חמשת הקבועים הבסיסיים של המתמטיקה, הידוע בשם זהות אוילר: $ {\displaystyle \ e^{i\pi }+1=0} $
הוכחת אי-רציונליות
בשנת 1737 הוכיח אוילר ש-e הוא מספר אי-רציונלי. הוכחתו התבססה על הצגתו של e כשבר משולב.[1] להלן הוכחתו המאוחרת יותר של ז'וזף פורייה לטענה זו. נניח בשלילה כי e הוא רציונלי. e הוא בבירור מספר חיובי, ולפיכך קיימים מספרים טבעיים a ו-b כך ש $ e={\frac {a}{b}} $. נסמן
- $ \,x=b!\left(e-\sum _{n=0}^{b}{\frac {1}{n!}}\right) $
- כעת נראה כי x הוא מספר שלם:
- $ x=b\,!\left(e-\sum _{n=0}^{b}{\frac {1}{n!}}\right)=b\,!\left({\frac {a}{b}}-\sum _{n=0}^{b}{\frac {1}{n!}}\right)=a(b-1)!-\sum _{n=0}^{b}{\frac {b!}{n!}} $
והביטוי האחרון הוא מספר שלם משום ש-n קטן או שווה ל-b.
- כפי שהוגדר לעיל, x הוא בבירור מספר חיובי. להלן נראה כי x קטן מ-1, ומכיוון שאין מספרים שלמים בין 0 ל-1 הרי שבכך נקבל סתירה ונסיק ש e הוא אי-רציונלי:
כזכור, $ e=\sum _{n=0}^{\infty }{\frac {1}{n!}} $, ולפיכך $ x=b!\sum _{n=b+1}^{\infty }{\frac {1}{n!}} $
לכן נוכל לכתוב:
$ {\begin{aligned}x=\sum _{n=b+1}^{\infty }{\frac {b!}{n!}}&={\frac {b!}{(b+1)!}}+{\frac {b!}{(b+2)!}}+\dots =\\&={\frac {1}{b+1}}+{\frac {1}{(b+1)(b+2)}}+{\frac {1}{(b+1)(b+2)(b+3)}}+\dots <\\&<{\frac {1}{b+1}}+{\frac {1}{(b+1)^{2}}}+{\frac {1}{(b+1)^{3}}}+\dots \end{aligned}} $
הביטוי האחרון הוא טור הנדסי שאיברו הראשון הוא $ {\frac {1}{b+1}} $ ומנתו היא $ {\frac {1}{b+1}}<1 $, ולפיכך, על פי נוסחת הסכום של טור הנדסי, סכומו הוא $ {\frac {\frac {1}{b+1}}{1-{\frac {1}{b+1}}}}={\frac {1}{b}} $ לכן $ x<{\frac {1}{b}}\leq 1 $, כלומר x הוא מספר חיובי שלם הקטן מ-1. זוהי סתירה ולפיכך e הוא מספר אי-רציונלי.
הוכחת טרנסצנדנטיות
העובדה שהקבוע e הוא מספר טרנסצנדנטי, מספר שאין אפשרות להגדיר אותו באמצעות פעולות אלגבריות של חיבור, חיסור, כפל, חילוק והעלאה בחזקה, נתגלתה בידי שארל הרמיט בשנת 1873. בהמשך המתמטיקאי פרדיננד לינדמן השתמש בעובדת היותו של e מספר טרנסצנדנטי ובאמצעות נוסחת אוילר הקושרת את הקבוע e עם הקבוע פאי, הוכיח שגם פאי הוא מספר טרנסצנדנטי.
שימושים
הקבוע e מופיע בניתוחים ומשמש בחישובים של בעיות מתחומים שונים, בעיקר מתחום הניתוח ההסתברותי, הכלכלה ומדעי החיים והטבע, הקשורים בגידול המשכי.
גידול המשכי
תהליכי גידול המשכי (נקראים גם גידול מעריכי או גידול אקספוננציאלי) הם תהליכי צמיחה בהם כמות הצמיחה הנוכחית תלויה באופן קבוע בכמות הצמיחה הקודמת. גידול המשכי מתואר כך: יחידה מקורית צומחת בקצב מסוים, וכל חלק חדש הנובע מהצמיחה, עם היווצרו צומח אף הוא באותו הקצב. בתחום הכלכלה ובחישובי ריבית דריבית היחידה המקורית נקראת הקרן. הקבוע e מתאר את כמות הצמיחה כאשר קצב הגידול הוא של הכפלה עצמית בתקופה הנמדדת.
דוגמה: יחידה מקורית צומחת ומכפילה את עצמה במהלך תקופה של אלף ימים. היחידה בנויה מאלף תתי יחידות, אשר לאחר אלף ימים ישוכפלו כולן. בכל יום משוכפלת תת-יחידה אחת, אך מיד עם שכפולה, ברגע שנוצרת תת-היחידה החדשה, גם זו תתחיל בשכפול עצמה בקצב של היחידה המקורית, כלומר ביום הבא, בנוסף לשכפול תת-יחידה, יחל שכפול של אלפית מתת היחידה הקודמת שנוצרה לפני יום.
וכך:
- ביום הראשון תשוכפל תת-יחידה אחת.
בסיכומו של היום הראשון נקבל 1.001 - ביום השני תשוכפל תת-יחידה אחת, אך בנוסף תצמח גם אלפית נוספת מתת היחידה של היום הראשון.
בסיכומו של היום השני נקבל 1.002001 - ביום השלישי תשוכפל תת-יחידה אחת, אלפית מכל אחת משתי תתי היחידה שהצטברו ביום השני, ובנוסף גם אלפית מן האלפית (כלומר אחד חלקי מיליון) שצמחה ביום השני.
בסיכומו של היום השלישי נקבל 1.003003001 - ביום הרביעי תשוכפל תת-יחידה אחת, אלפית מכל שלש תתי היחידה שהצטברו ביום השלישי, אחד ממיליון מכל אחד משלש האלפיות שהצטברו, ועוד חלק אלפית המיליון מחלק המיליון שנוסף ביום השלישי.
בסיכומו של היום הרביעי נקבל: 1.004006004001
וכן הלאה.
לאחר אלף ימים, בנוסף ליחידה המשוכפלת יהיו גם תתי היחידות הנוספות שצמחו. סך כל הצמיחה שנוצרה יהיה e, מעט יותר מפעמיים וחצי מספר תתי היחידות המקורי, ובקירוב: 2718 תתי יחידות, חישוב מקורב של e כפול אלף.
הגידול ההמשכי יכול לתאר תהליכי צמיחה, כאשר כל העת מתווספות יחידות חדשות, או דעיכה, כאשר יחידות הולכות ונחסרות.
גידול המשכי קיים בתחומים רבים, בהם בטבע ובעולם החי, בנוסחאות מתמטיות וחישוביות, וכן בתופעות אקראיות החוזרות על עצמן ומצטברות. משום כך הקבוע e מופיע בחישובי הסתברות, בניתוחי צמיחה בכלכלה ובמדעי הטבע החיים והסביבה, ותופס מקום חשוב בחשבון דיפרנציאלי ואינטגרלי.
ריבית דריבית
בחישובי ריבית דריבית e מהווה קבוע לחישוב החוב כעבור זמן מסוים או כעבור מספר מחזורים מסוים. הקבוע e נתגלה בידי יאקוב ברנולי בעת ניתוח חישובי ריבית דריבית.
לדוגמה, אם אדם מפקיד בבנק סכום של שקל אחד (הקרן היא שקל אחד) ומקבל ריבית של 100% המחושבת אחת לשנה, הוא יצבור סכום של שני שקלים בסוף השנה. אם הבנק יחשב את הריבית מדי חצי שנה בריבית דריבית, כלומר ריבית של 50% בחצי הראשון של השנה שלאחריו יהיה בבנק שקל וחצי, וחישוב ריבית של 50% בחצי השני של השנה, הפעם 50% על שקל וחצי, שהם 50% על הקרן – השקל, ועוד 50% על הריבית שנצברה – חצי השקל שהתקבל בחלק הראשון של השנה. בתום החצי השני של השנה יהיו ברשותו 2.25 שקלים. אם חישוב הריבית יבוצע מדי רבע שנה, יסיים עם 2.44 שקלים. אם חישובי הריבית יבוצעו במרווחי הזמן הקטנים ביותר הסכום שיתקבל יתקרב ל-e כפול הקרן. בדוגמה שלנו הקרן הוא שקל אחד, ולכן בסוף השנה המפקיד יקבל מהבנק e שקלים לפי הנוסחה: $ e=\lim _{n\to \infty }\left(1+{1 \over n}\right)^{n} $ שהם בקירוב 2 שקלים ו-72 אגורות.
חישובי הסתברות
התפלגות נורמלית
בתורת ההסתברות, פונקציית צפיפות ההסתברות של התפלגות נורמלית נתונה על ידי $ {\displaystyle \ f(x)={\frac {1}{\sqrt {2\pi \sigma ^{2}}}}e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}} $ פונקציה זו נקראת "פעמון גאוס" או "גאוסיאן" על שם המתמטיקאי הנודע קרל פרידריך גאוס. פונקציה זו שימושית ביותר – הן לצורכי תאוריה והן לצרכים ניסיוניים, שכן לפי משפט הגבול המרכזי הממוצע של מספר גורמים אקראיים, בלתי תלויים ובעלי אותה התפלגות, שואף לאחר נירמול מתאים להתפלגות נורמלית.
הקבוע e משמש גם כאן, כתוצאה מ'גידול המשכי' בהגדרת פעמון גאוס, כאשר הצמיחה הולכת וקטנה בתלות בצמיחה הקודמת, ובכך מגדירה את צורת העקומה.
הסתברות לזכייה של אדם המשתתף במספר רב של הגרלות
נניח שאדם מסוים משתתף באופן עקבי בהגרלות כך שבסופו של דבר הוא צפוי להשתתף ב- $ \,n $ הגרלות. נניח שההסתברות של אותו אדם לזכות בהגרלה בודדת היא $ \,p={k \over n} $. לצורך הפשטות, נניח הנחה ריאלית ש-$ \,{0<k<1} $. הקבוע e משמש לחישוב הסתברות שאותו אדם יזכה מתוך כל ההגרלות שבהן ישתתף לפחות בהגרלה אחת. אם נניח שאין תלות בין התוצאות של ההגרלות וש-$ \,n $ הוא מספר מספיק גדול, אז ההסתברות שמשתתף מסוים לא יזכה באף אחת מההגרלות, קרובה ל- $ \,{\frac {1}{e^{k}}} $ וההסתברות שאותו המשתתף יזכה לפחות באחת מההגרלות היא בקירוב $ 1-{\frac {1}{e^{k}}} $.
החישוב:
אם משתתף מסוים משתתף ב-$ \,n $ הגרלות, ההסתברות שהמשתתף לא יזכה באף אחת מן ההגרלות מחושבת כך:
- ההסתברות של האדם לזכות בִהגרלה מסוימת היא $ \,p={k \over n} $.
- ההסתברות שהאדם לא יזכה בהגרלה מסוימת היא $ 1-p=1-{k \over n} $.
- כאמור בהנחה שאין תלות בתוצאות של כל ההגרלות, ההסתברות שהאדם לא יזכה באף אחת מ- $ \,n $ הגרלות שבהן השתתף היא $ \left(1-{k \over n}\right)^{n} $.
- כאשר $ \,n $ שואף לאינסוף ו- $ \,k $ נשאר קבוע, גבול ההסתברות שמשתתף מסוים לא יזכה באף אחת מההגרלות, כאשר $ \,n $ שואף לאינסוף, הוא:
דוגמה:
נניח שאדם משתתף ב-$ \,n=2,500 $ הגרלות, כשהסתברות הזכייה שלו בהגרלה בודדת היא $ \,p=10^{-4} $. בתנאים אלו,
$ \,k=np=0.25 $. ההסתברות שלא יזכה באף אחת מההגרלות היא בקירוב $ \,{\frac {1}{e^{k}}}\cong 0.779 $. ההסתברות שהאדם יזכה בהגרלה אחת לפחות היא $ \,1-{\frac {1}{e^{k}}}\cong 0.221 $.
בעיית הדוור
 ערך מורחב – בלבול (קומבינטוריקה)
ערך מורחב – בלבול (קומבינטוריקה)
בעיה דומה לבעיה הקודמת, נתגלתה בידי פייר ריימונד דה מונטמורט יחד עם ברנולי, ונקראת בעיית הדוור, או בעיית 'בדיקת הכובעים':
דוור מבולבל מחלק באקראי n מכתבים ל-$ \,n $ תיבות. הקבוע e משמש לחישוב ההסתברות שאף מכתב לא יגיע ליעדו.
את חישוב ההסתברות ניתן למצוא באמצעות עקרון ההכלה וההפרדה. מקבלים כי ההסתברות שווה לסכום הטור:
טור זה הוא טור טיילור של הפונקציה $ \ e^{-x} $ בנקודה 1 (או טור טיילור של הפונקציה $ \ e^{x} $ בנקודה $ \,-1 $). על כן, כאשר $ \,n $ שואף לאינסוף, שואף סכום הטור ל-$ {\frac {1}{e}} $.
חישוב עצרת לערכים גדולים (נוסחת סטירלינג)
נוסחת סטירלינג נותנת קירוב לפונקציית העצרת. במשפט אודות העצרת נקבע כי עבור $ \ n $ גדול, מתקיים $ n!\approx {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n} $. את המשפט מוכיחים בעזרת פונקציית גמא (המאפשרת ליצור הכללה של פונקציית העצרת למספרים שאינם שלמים): $ {\displaystyle \ \Gamma (n+1)=\int _{0}^{\infty }t^{n}e^{-t}\,\mathrm {d} t} $ אשר עבור n טבעי מקיימת: $ \ \Gamma (n+1)=n! $.
כל מספר עצרת, מכפיל את כל המספרים הקודמים לו,
- $ a_{n}=n=(n-1)+1=a_{n-1}+1 $
- $ x!=a_{1}(a_{1}+1)((a_{1}+1)+1)...(((...a_{1}+1)+1)+...) $
וכך עצרת למעשה מהווה פונקציה הקשורה בגידול המשכי, ומכאן הקשר לקבוע e.
חישובים במדעי הטבע והחיים
בפיזיקה
הקבוע e משמש לחישוב דעיכת מהירות חלקיק בזמן, בעקבות חיכוך המשכי, על פי חוקי ניוטון.
לפי החוק השני של ניוטון, התאוטה (כלומר השינוי במהירות) של חלקיק הנע בהשפעת כוח חיכוך המתכונתי למהירותו (כלומר כאשר כוח החיכוך תלוי במהירות הנוכחית), נקבע לפי:
$ {\displaystyle \ m{\frac {\mathrm {d} v}{\mathrm {d} t}}=-\mu v} $
כאשר $ \ v $ מהירות החלקיק, $ \ m $ המסה שלו ו-$ \ \mu $ מקדם החיכוך. המהירות החדשה, בהנחה שהמהירות ההתחלתית של החלקיק היא $ \ v_{0} $ הוא:
כלומר, המספר $ \ e $ משמש לתיאור דעיכת מהירות החלקיק בזמן.
כמו כן, הקבוע משמש למדידת הדעיכה של זרם כפונקציה של זמן במעגל חשמלי במהלך טעינה או פריקה של קבל לפי נוסחה דומה: $ \ I(t)=I_{0}e^{-{\frac {t}{\tau }}} $ כאשר $ I_{0} $ הוא הזרם ההתחלתי ו-$ \tau $ הוא קבוע הזמן ששווה ל-$ RC $ – הנגד השקול במעגל כפול הקיבול של הקבל השקול.
במדעי החיים והסביבה
הקבוע e משמש לחישוב הצמיחה והדעיכה של אוכלוסיות, צמחים, איברים ובעלי חיים, כאשר מדובר בתהליכי גידול המשכי. אלו קיימים במקרים רבים בעולם החי, כאשר תאים משכפלים את עצמם ומכפילים את כמותם בקצב קבוע, וגם כאשר התופעות הנמדדות אינן של הכפלה עצמית, אך קצב הצמיחה או הדעיכה שלהן תלוי באוכלוסייה הקודמת. בחישובים אלו, $ g=ce^{f(x)} $ מגדיר את הגדילה, כאשר
- g הוא התוצר (growth),
- c הוא קבוע כלשהו הקשור לקצב הגדילה, ובנוסף,
- (f(x היא פונקציה המגדירה את מספר המחזורים וקצב הגדילה.
במדעי הסביבה, וכן בחישובי התפשטות מחלות במדעי הרפואה, במצבים של משאב מתכלה גידול האוכלוסייה בזמן נתון לפי עקומת גאוס, שנוסחתה תלויה בקבוע e, כאשר בתקופת הצמיחה האוכלוסייה צומחת בגידול המשכי, ואילו לאחר הרוויה היא דועכת באופן דומה.
במתמטיקה
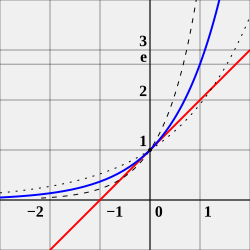
כאמור, הקבוע e הוא המספר היחיד שאם מציבים אותו במקום $ a $ בפונקציה $ f(x)=a^{x} $ וגוזרים את הפונקציה לפי $ x $, תתקבל אותה פונקציה עצמה. במילים אחרות, השיפוע של הגרף של $ y=e^{x} $ בכל נקודה נתונה שווה בערכו לגובה הגרף באותה נקודה. בשל כך, הוגדר הלוגריתם הטבעי להיות לוגריתם בבסיס e, והוא בעל חשיבות גדולה בענפי מתמטיקה רבים, בהם חשבון אינפיניטסימלי, ובמיוחד לגבי מספרים מרוכבים – הצגת המספרים המרוכבים באופן גאומטרי, וחישובי פונקציות עם מספרים מרוכבים.
נוסחת אוילר וזהות אוילר
באמצעות הגדרתו במשפט טיילור של הקבוע e, ניתן להסיק את משפט אוילר הקובע כי $ e^{ix}=\cos x+i\sin x $ לכל x שהוא.
המקרה הפרטי בו $ x=\pi $ נקרא זהות אוילר, הקובעת כי $ e^{i\pi }+1=0 $, וקושרת חמישה קבועים חשובים במתמטיקה: היחידה (המספר אחד), אפס, קבוע אוילר, פאי (היחס בין הקוטר להיקף המעגל) והיחידה המדומה (המספר $ i $).
ייצוג גאומטרי של מספרים מרוכבים באמצעות הקבוע e
 ערך מורחב – מספר מרוכב
ערך מורחב – מספר מרוכב
בייצוג גאומטרי של מספרים מרוכבים במישור המרוכב, חיבור שקול לתזוזה במישור המרוכב בשיעור אחד המספרים, ותזוזה נוספת בשיעור המספר האחר. תוצאת פעולת הכפל היא מספר שגודלו הוא מכפלת הערכים המוחלטים של שני המספרים, והזווית שלו מחלקו החיובי של הציר האופקי ("ציר ה-x") היא סכום זוויות אלו של שני המספרים.
בנוסף, ניתן להגדיר כל מספר מדומה $ z $ באמצעות הגאומטריה במישור המרוכב:
- $ z=r(\cos \varphi +i\sin \varphi )\, $ כאשר,
- $ r $ הוא הגודל המוחלט (ובשמות אחרים: המרחק, המקדם או המודולוס) של המספר המרוכב, והוא מסומן גם כ-$ |z| $.
- $ \varphi $ הוא הפאזה (או הזווית או הארגומנט) שלו, ומסומן גם כ-$ \mathrm {arg} (z) $.
מכאן, לפי משפט אוילר, ניתן לייצג את אותו המשתנה z באמצעות הנוסחה:
- $ z=re^{i\varphi }\, $
בכיוון ההפוך, ניתן לעבור ליצוג המספרים המרוכבים דרך המתמטיקה של חזקות הקבוע e. אם $ w=a+ib $ הוא מספר מרוכב כלשהו, כך ש-$ a $ ו-$ b $ הם ממשיים, אז מגדירים, כמו במספרים הממשיים,
- $ z=e^{w}=e^{a+ib}=e^{a}e^{ib} $
ולכן מתקיים:
- $ a=\ln |z| $
- $ b=\mathrm {arg} (z) $
בעקבות הזהות הזו, וכללי החזקה המתקיימים גם במספרים מרוכבים, ניתן להבין את הסיבה לפעולת החיבור בין הזוויות הנדרשת כדי לפתור פעולת כפל בין שני מספרים מרוכבים, כפי שמחברים את המעריכים כאשר שני מספרים בעלי אותו הבסיס (במקרה זה הקבוע $ e $) מוכפלים זה בזה. באותו הזמן פעולת הכפל הרגילה נדרשת על מנת לבצע את מכפלת הערכים (המרחקים). באופן זה בייצוג הגאומטרי על המישור המרוכב, פעולות מכפלה של מספרים מרוכבים הופכות לפעולות סיבוב (רוטציה) ומתיחה (סקאליזציה).
קוריוזים מתמטיים
לכל $ x $ מתקיים $ e^{x}\geqslant x^{e} $. זהו המספר היחיד המקיים תכונה זו.
בדומה לקירוב הידוע של $ \pi $ $ \ {\frac {355}{113}} $, הנותן את $ \pi $ בדיוק של 6 ספרות מימין לנקודה העשרונית, קיים הקירוב ל-$ e $: $ \ {\frac {878}{323}}=2.718266... $, הנותן את e בדיוק של 4 ספרות מימין לנקודה העשרונית.
המספר $ \ e^{\pi } $ (או $ (-1)^{i} $ לפי זהות אוילר) ידוע כקבוע גלפונד, והטרנסצנדנטיות שלו נובעת ממשפט גלפונד-שניידר. על המספר $ \ \pi ^{e} $ לא ידוע האם הוא אלגברי או טרנסצנדנטי.
e בפולקלור
למרות חשיבותו של הקבוע $ e $ הוא פחות ידוע יחסית לקבוע π (פַּאי), המופיע רבות בפולקלור המתמטי. זריקת עידוד לפרסומו ניתנה על ידי חברת גוגל, שבהנפקת ניירות ערך הראשונה שלה, ציינה את סכום ההנפקה כ-$2,718,281,828, קירוב של e מיליארד דולר. שימוש נוסף שגוגל עשו במספר הוא פרסום מודעה גדולה בלב עמק הסיליקון הקוראת לגלוש לאתר שכתובתו "עשר הספרות הרצופות הראשונות במספר e היוצרות יחדיו מספר ראשוני" (התשובה מגיעה רק בספרה ה-101: 7427466391). מי שפתר את החידה נשלח לפתור חידה קשה יותר, ורק אז הגיע לאתר של Google Labs שם הוזמן לשלוח קורות חיים כדי להתקבל לעבודה אצלם.
מדען המחשב דונלד קנות' ממספר את הגרסאות של תוכנת Metafont כך שילכו ויתקרבו ל-e: גרסה 2, גרסה 2.7, גרסה 2.71, וכו'. נכון ל-2020, הגרסה היציבה האחרונה (מתאריך 2014-01-07) היא 2.7182818.
ראו גם
לקריאה נוספת
- Eli Maor, e: The Story of a Number, Princeton University Press, 1994. מסת"ב 0-691-05854-7
קישורים חיצוניים
- ממיליון ועד עשרה מיליון הספרות הראשונות של e
 e ומספרים טרנסצנדנטיים, סרטון באתר יוטיוב (באנגלית)
e ומספרים טרנסצנדנטיים, סרטון באתר יוטיוב (באנגלית) ניסיון לתאר את זהות אוילר והקבוע e, באופן פשוט ומובן, סרטון באתר יוטיוב (באנגלית)
ניסיון לתאר את זהות אוילר והקבוע e, באופן פשוט ומובן, סרטון באתר יוטיוב (באנגלית) קבוע אוילר, סרטון באתר יוטיוב
קבוע אוילר, סרטון באתר יוטיוב- E, באתר MathWorld (באנגלית)
- סדרת הספרות של הקבוע e באתר OEIS – האנציקלופדיה המקוונת לסדרות של מספרים שלמים
 ריבית דריבית והמספר e | החסכן המשקיען | פרק 4, סרטון בערוץ "דביר רוס", באתר יוטיוב
ריבית דריבית והמספר e | החסכן המשקיען | פרק 4, סרטון בערוץ "דביר רוס", באתר יוטיוב
הערות שוליים
- ↑ Ed Sandifer, How Euler Did It: Who proved e is Irrational?, MAA Online, February 2006
| מספרים אי-רציונליים נודעים | ||
|---|---|---|
| מספרים אלגבריים | 2√ • 3√ • יחס הזהב 𝜑 • יחס הכסף δAg • היחס הפלסטי 𝜌 | 
|
| מספרים טרנסצנדנטיים | בסיס הלוגריתם הטבעי 𝑒 • פאי 𝜋 • קבוע גאוס • קבוע אומגה Ω • קבוע ליוביל | |
| מספרים אי-רציונליים, שלא ידוע האם הם אלגבריים או טרנסצנדנטיים |
קבוע אפרי (3)ζ • קבוע ארדש-בורוויין | |
| טריגונומטריה | קבועים טריגונומטריים מדויקים | |
E (קבוע מתמטי)36208916Q82435
