אפיגרף (מתמטיקה)
מראה
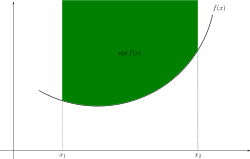
במתמטיקה, האֶפִּיגְרָף של פונקציה f : Rn→R היא קבוצת הנקודות שנמצאות מעל או על הגרף:
האפיגרף המוגבל הוא האפיגרף ללא הגרף עצמו:
הגדרה זהה קיימת לפונקציה שלוקחת ערכים מהתחום R ∪ ∞., ובמקרה זה, האפיגרף הוא הקבוצה הריקה אם ורק אם f זהה לאינסוף (). אפשר גם להגדיר את האפיגרף כאשר התמונה היא כל מרחב וקטורי. בצורה דומה, אפשר להגדיר את קבוצת הנקודות שמתחת לגרף, שהיא ההיפוגרף. מאפיינים של האפיגרף הם:
- פונקציה היא קמורה אם ורק אם האפיגרף שלה היא קבוצה קמורה.
- פונקציה היא פונקציה רציפה למחצה אם ורק אם האפיגרף שלה היא קבוצה סגורה.
אפיגרף (מתמטיקה)41928905Q1347059


