רשת עצבית מלאכותית

תרשים המדגים את אופן הפעולה של רשת עצבית מלאכותית.

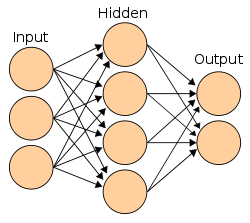
רשת עֲצַבִּית מלאכותית (ANN – Artificial Neural Network), רשת נוירונים או רשת קשרית הוא מודל מתמטי חישובי, שפותח בהשראת תהליכים מוחיים או קוגניטיביים המתרחשים ברשת עצבית טבעית ומשמש במסגרת למידת מכונה. רשת מסוג זה מכילה בדרך כלל מספר רב של יחידות מידע (קלט ופלט) המקושרות זו לזו, קשרים שלעיתים קרובות עוברים דרך יחידות מידע "חבויות" (Hidden Layer). צורת הקישור בין היחידות, המכילה מידע על חוזק הקשר, מדמה את אופן חיבור הנוירונים במוח. השימוש ברשתות עצביות מלאכותיות נפוץ בעיקר במדעים קוגניטיביים, ובמערכות תוכנה שונות – בהן: מערכות רבות של אינטליגנציה מלאכותית המבצעות משימות מגוונות – זיהוי תווים, זיהוי פנים, זיהוי כתב יד, חיזוי שוק ההון, מערכת זיהוי דיבור, זיהוי תמונה, ניתוח טקסט ועוד.

רקע

ערך מורחב – רשת עצבית

רשת עצבית היא רשת של מעבדים מקושרים: כל מעבד ברשת מסוגל לבצע פעולה מתמטית פשוטה, אך בהיקשרם יחד הם מסוגלים להתנהגות מורכבת.

רשת עצבית טיפוסית

במוח, תאי עצב או נוירונים הם התאים שמהם מורכבת מערכת העצבים, ויש כמאה מיליארד מהם אצל אדם ממוצע. כל אחד מהם התפתח להיות מעבד אלקטרוני. הדֶנדריטים מקבלים מידע מהעולם החיצון ומהווים את מערכת הקלט של הנוירון. כשמתקבלים מספיק גירויים בדנדריטים, גוף התא מייצר אות חשמלי שנע לאורך האַקסוֹן לדנדריטים של תאים אחרים או לשרירים ומגרה אותם. ככל שהנוירונים מקבלים יותר גירויים מהדנדריטים, הם מייצרים יותר אותות חשמליים בשנייה אחת.

כיצד נוירון מעבד מידע

ההבדל העיקרי ביותר בין רשת עצבית ביולוגית לבין רשת עצבית מלאכותית הוא שמחשבים פועלים בעיקר בעיבוד טורי, או עם כמות קטנה של עיבוד מקבילי, ואילו מוחות של יצורים פועלים בעיבוד מקבילי. על פי התזה של צ'רץ' וטיורינג, המודל שקול למכונת טיורינג, (כיוון שכל חישוב שיכול להעשות בידי מחשב מקבילי יכול להעשות גם בידי מחשב טורי).

ישנם עוד כמה הבדלים חשובים בין רשתות עצביות במוח לרשתות מלאכותיות. במוח יש מספר עצום של מרכיבים (בערך 10¹¹), שכל אחד מהם מחובר למרכיבים רבים (בין 1,000 ל־10,000 בממוצע). כל אחד מהמרכיבים האלה מבצע חישוב פשוט למדי, שטבעו עדיין אינו ברור לחלוטין, יחסית באיטיות (פחות מקילוהרץ אחד), המבוסס בעיקר על מידע שהוא מקבל מהחיבורים המקומיים שלו. במערכות מלאכותיות, תאי העצב מחוברים ביניהם באופן אחיד, וכולם מבצעים את אותה הפעולה החישובית. לכל חיבור מיוחס משקל מספרי כלשהו. הפלט של כל תא הוא ערך מספרי יחיד, שמחושב כתוצאה של סכום הפעולות של תאי הקלט והמשקל היחסי שלהם. אפשר גם לחלק את רשתות תאי העצב לשתי קבוצות שונות, בעלות למידה מונחית או לא מונחית. רשתות מונחות, כמו הפרספטרון, משתמשות באלגוריתם למידה מונחה, כלומר שהמערכת צריכה לקלוט ולפלוט מידע בשלב הלמידה. לעומת זאת, רשתות לא מונחות, כמו רשת קוהונן, מצריכות רק שמידע יקלט, ללא פלט. מערכות אלה מארגנות את המידע הנקלט בעצמן, על פי מדד דמיון.

היסטוריה

פרק זה לוקה בחסר. אנא תרמו למכלול והשלימו אותו. ייתכן שתמצאו פירוט בדף השיחה. הסיבה היא: פרק ההיסטוריה נפסק באמצע וחסר התפתחויות חשובות משנות האלפיים.

שנת 1943 – ההתפתחות מדע רשתות העצביות

בשנת 1943 פרסמו שני חוקרים אמריקאים, ורן מקלוך וולטר פיטס מאמר, שהיווה בסיס להתפתחותו של מדע הרשתות העצביות. המאמר הציע מודל פשוט של פעולת הנוירון, שעליו מבוססות הרשתות המלאכותיות עד היום:

דוגמה לנוירון מלאכותי בסיסי. ארבעה נתוני קלט, המסומנים ב: i₁ עד i₄. אלו מייצגים את הדנדריטים ויכולים להיות מחוברים לעולם החיצון או לנוירונים אחרים. לקלט "משקל" יחסי, המבוטא על ידי משקולות המסומנות ב: w₁ עד w₄. משקולות אלו מייצגות את עוצמת הקשרים בין הדנדריטים של נוירון אחד לגוף התא בנוירון אמיתי שני

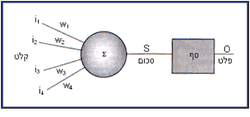
הנוירון מקבל קלטים (נהוג לסמן ב־i), כשלכל אחד מהם משקל יחסי (נהוג לסמן ב־w). כל נתון נשקל על ידי הכפלתו במשקולת המתאימה לו, כאשר התוצאה מסכום הקלטים המשוקללים:

סכום = $\langle i,w\rangle =\sum _{j}i_{j}w_{j}=O$.

אם סכום זה (המהווה במובן הביולוגי את הגירוי הכולל המגיע לנוירון) גבוה מסף ידוע כלשהו, הנוירון מעביר פלט "1"; אם לא, הפלט הוא "0".

תהליך זה מזכיר פעולה של נוירון אמיתי, המפיק אות חשמלי כשהגירוי מספיק.

שימוש בנוירון לזיהוי תבנית. ניתן לקודד את הפיקסלים הכהים ב־1 ואת הבהירים ב־0. כעת, אם נחבר את הנוירון שלנו כמוצג בשרטוט ב', הוא ייתן פלט "1" בכל פעם שיראה תבנית זו. גם אם התבנית אינה מושלמת – האחדים אינם בדיוק אחד, והאפסים אינם בדיוק אפס – הנוירון עדיין יזהה את התבנית (במקרה זה נאמר, כי הנוירון עמיד לרעש). אולם, אם נכניס תבנית שונה לחלוטין כמו זו המוצגת בשרטוט 6ג', הנוירון לא יזהה אותה.

סידור המשקולות מהותי לתפקוד הרשת. המשקולות הן אלו שקובעות מהי התבנית שתזוהה, וקביעתן היא המשימה המרכזית של תוכנית הרשת העצבית.

שנת 1969 – נטישת הרשתות בעקבות מאמר על המגבלות ברשתות נוירונים

בשנת 1969 פרסמו מרווין מינסקי וסימור פפרט (Minsky and Papert) את ספרם "Perceptrons", שבו תקפו את הרעיונות העומדים מאחורי הרשתות העצביות. הספר הציג פגם בנוירון הבסיסי.

הבעיה הייתה זו: לא משנה אילו משקולות נשים על הקלט, לא נוכל ליצור את השער הלוגי Exclusive OR) XOR) עבור רשת עם שכבה יחידה. בנוסף טענו, שלמחשבים אין די כוח חישוב כדי להתמודד עם רשתות מורכבות. טיעונים אלו ונוספים עיכבו את המשך התפתחותן של הרשתות העצביות במשך שנים רבות. חוקרים רבים נטשו את התחום בחשבם כי אם הנוירון לא יכול לבצע משימה פשוטה זו, אין טעם בהמשך המחקר.

למעשה, מה שהיה נחוץ כדי להתגבר על בעיה זו ועל בעיות דומות לה הוא לא נוירון אחד, כי אם רשת של נוירונים, והמתמטיקאי הרוסי אנדריי קולמוגורוב כבר הראה כי רשת נוירונים ב־3 שכבות תוכל לפתור XOR.

נוירון יחיד אינו יכול לדַמוֹת שער XOR

רשת עצבית רב־שכבתית

שנת 1982 – עלייתן מחדש של רשתות הנוירונים בשנות השמונים

אף על פי שהפתרון היה ידוע, רק בשנים 1982–1983 התעורר שוב העניין במחקר הרשתות העצביות. בזמן זה, "אלגוריתם הפעפוע לאחור" זכה לפרסום נרחב.

דוגמה לרשת עצבית

שנות האלפיים – למידה עמוקה

רשתות עצביות מלאכותיות זכו לעדנה מחודשת החל מהעשור הראשון של שנות ה־2000. בתקופה זו החל שימוש פופולרי במושג "deep belief nets" ובקיצור רשתות עמוקות שנטבע במאמר המשפיע מ־2006 של הינטון, אוסינדרו וטה. במסגרת למידה עמוקה נעשה נפוץ השימוש ברשתות עצביות מלאכותיות שבהן מספר שכבות חבויות. מאז 2012, כל המנצחות בתחרויות ראייה ממוחשבת גדולות בתחום זיהוי אובייקטים, כגון תחרות ImageNet, מבוססות על למידה עמוקה. מאז שב-2012, "למידה עמוקה" הצליחה לשפר את אחוזי הדיוק בבעיות זיהוי עצמים, תחרות ImageNet, ארכיטקטורות הרשתות זכתה לתשומת לב רבה, הן באקדמיה והן בתעשייה.

מבנה רשת עצבית

רשת נוירונים מורכבת ממספר רב של תאי בסיס, כך שכל תא בסיס מבצע חישוב פשוט יחסית. לכל תא מספר כניסות ויציאה אחת שערכה הוא פונקציה כלשהי של הכניסות. יציאה של תא מסוים יכולה להזין מספר כניסות של תאים שונים.

ישנם מודלים רבים של רשתות עצביות. המשותף לכולם הוא קיומן של יחידות עיבוד בדידות (המקבילה במודל לנוירונים הביולוגיים) הקשורות ביניהן בקשרים (בדומה לקשרים הקיימים בין הנוירונים הביולוגיים). הפרטים – מספר הנוירונים, מספר הקשרים, מבנה הרשת (סידור בשכבות, מספר השכבות) – משתנים ממודל למודל. מקובל להשתמש בכלים מתחום האלגברה הליניארית כגון מטריצות ווקטורים על־מנת לייצג את הנוירונים והקשרים ביניהם. הפעולה שמבצע כל נוירון על הקלט שלו בדרך כלל מיוצגת על ידי פונקציה.

רשת נוירונים מאופיינת על ידי:

• חיבורים – אופן החיבור בין הנוירונים ברשת
• משקלים – השיטה הקובעת את משקלי החיבורים בין הנוירונים
• פונקציית האקטיבציה, העשויה להיות שונה בכל שכבה (פונקציה לא ליניארית, לרוב logsig או סיגמואיד)

רשתות נוירונים מורכבות ממספר רב של יחידות עיבוד פשוטות הנקראות נוירונים, אשר מחוברות באופן היררכי ומובנות בשכבות. השכבה הראשונה נועדה לקלוט מידע לרשת, השכבה האמצעית ידועה כשכבה החבויה (במודלים שונים עשויים להיות יותר מאחת כזו), ולבסוף השכבה האחרונה אשר נועדה להחזיר את המידע המעובד כפלט. הצמתים בכל שכבה מחוברים באופן מלא לצמתים בשכבות הסמוכות באמצעות חיבור ישיר בין הנוירונים, כאשר לכל קשר קיים משקל מסוים. המשקל בכל קשר קובע עד כמה רלוונטי המידע שעובר דרכו, והאם על הרשת להשתמש בו על מנת לפתור את הבעיה. כל צומת בשכבת הקלט (השכבה הראשונה) מייצג תכונה שונה מהמבנה, ושכבת הפלטים מייצגת את הפתרון של הבעיה. בשכבה האמצעית והחיצונית קיימים "ערכי סף" הניתנים לכיול במערכת ממוחשבת, וקובעים את חשיבות הקשרים השונים,

ברשת ישנם שלושה סוגי שכבות:

1. שכבת כניסה (Input Layer) – לכל תא בשכבה זו כניסה אחת. וקטור הכניסות הוא הקלט לרשת. מספר התאים: כמספר המאפיינים (Features). מומלץ לבצע מחקר בנוגע להשפעתם של המאפיינים השונים על השגיאה, הקשרים וההיררכיה ביניהם. כלל אצבע הוא כי המספר הכולל של המאפיינים לא יעלה על עשירית ממספר הדוגמאות בסדרת הלימוד.
2. שכבות חבויות (Hidden Layers) – לכל תא בשכבה זו מספר כניסות, כמספר תאי הכניסה (Fully Connected). רשת נוירונים ללא שכבות חבויות מאוד מוגבלת והיא נקראת פרספטרון. מספר התאים: כמספר התאים בשכבת הכניסה בתוספת תא אחד או שניים. מספר השכבות: מ־0 ועד לאינסוף. בכל השכבות החבויות בדרך כלל אותו מספר תאים. מומלץ לבצע מחקר בנוגע להשפעתם של מספר התאים ומספר השכבות החבויות על השגיאה. מספר השכבות ומספר התאים מגדירים את גודל הרשת. יש לבחור רשת גדולה מספיק, אך לא גדולה מדי. רשת קטנה מדי לא תוכל לקרב בדיוק מספיק את המיפוי הנדרש, ואילו רשת גדולה מדי תמנע לימוד יעיל (זהו ה־Bias Trade Off). רשתות רב־שכבתיות אופייניות הן בעלות שכבה חבויה אחת או שתיים, ומספר הנוירונים בשכבות הנסתרות במקרים רבים אינו עולה על 10 (אלא אם כן קיימת חלוקה מודולרית למספר תת־רשתות). בעיות זיהוי תמונה בדרך כלל מאופיינות עם מספר שכבות גבוה מאוד (מאות שכבות). כוונון מספר הנוירונים ומבנה הרשת יעשה לרוב אמפירית, תוך שימוש בדוגמאות ולידציה (Validation) או באמצעות אימות־צולב (Cross Validation).
3. שכבת יציאה (Output Layer) – לכל תא בשכבה זו מספר כניסות, כמספר תאי השכבה המוסתרת (Fully Connected). וקטור מוצאי התאים בשכבה זו הוא וקטור היציאה של הרשת. מספר התאים: כמספר ה־Classes.

פונקציית אקטיבציה

כמה מהתכונות שעשויות להיות שימושיות לפונקציית אקטיבציה:

• לא ליניארית – כאשר הפונקציה אינה ליניארית, ניתן להוכיח שרשת עצבית של שתי שכבות היא משערך אוניברסלי. פונקציית הזהות אינה מקיימת את תכונה זו. כאשר מספר שכבות משתמשות באקטיבציה של פונקציית זהות, הרשת שקולה למודל של שכבה אחת.
• גזירה ברציפות – זו תכונה רצויה המסייעת לאופטימיזציה מבוססת גרדיאנט. פונקציה מדרגה בינארית אינה גזירה ב-0, והנגזרת שלה היא 0 עבור ערכים אחרים, ולכן שיטות מבוססות גרדיאנט עשויות להיתקע.
• טווח – כאשר הטווח של פונקציית האקטיבציה סופי, שיטות אימון מבוססות גרדיאנט נוטות להיות יציבות יותר, כי ייצוג התבנית מושפע מאוד ממשקולות מוגבלים. כאשר הטווח אינסופי, האימון בדרך כלל יעיל יותר כיוון שייצוג תבניות משפיע על רוב המשקולות.
• מונוטונית – כאשר פונקציית האקטיבציה היא מונוטונית, שטח השגיאה הקשור במודל עם שכבה יחידה מובטח להיות קמור.
• קרובות לזהות ליד נקודת הראשית – כאשר פונקציית האקטיבציה ניחנת בתכונה זו, הרשת לומדת ביעילות כאשר המשקולות מאותחלים לערכים אקראיים קטנים. כאשר תכונה זו לא מתקיימת בפונקציית האקטיבציה, נדרשת תשומת לב באתחול ערכי המשקולות. בטבלה שלהלן, פונקציות אקטיבציה שבהן $f(0)=0$ וגם $f'(0)=1$ וגם $f'$ רציפה ב-0 מופיע סימון הרומז על קיום תכונה זו.

הטבלה הבאה משווה את התכונות של מספר פונקציות אקטיבציה:

שם	איור	משוואה	נגזרת (ביחס ל x)	טווח	פונקציה חלקה	מונוטונית	נגזרת מונוטונית	קרובות לזהות ליד הראשית
זהות		$f(x)=x$	$f'(x)=1$	$(-\infty ,\infty )$	$C^{\infty }$	כן	כן	כן
מדרגה		$f(x)={\begin{cases}0&{\text{for }}x<0\\1&{\text{for }}x\geq 0\end{cases}}$	$f'(x)={\begin{cases}0&{\text{for }}x\neq 0\\?&{\text{for }}x=0\end{cases}}$	$\{0,1\}$	$C^{-1}$	כן	לא	לא
לוגיסטית (או סיגמואיד)		$f(x)=\sigma (x)={\frac {1}{1+e^{-x}}}$	$f'(x)=f(x)(1-f(x))$	$(0,1)$	$C^{\infty }$	כן	לא	לא
TanH		$f(x)=\tanh(x)={\frac {(e^{x}-e^{-x})}{(e^{x}+e^{-x})}}$	$f'(x)=1-f(x)^{2}$	$(-1,1)$	$C^{\infty }$	כן	לא	כן
ArcTan		$f(x)=\tan ^{-1}(x)$	$f'(x)={\frac {1}{x^{2}+1}}$	$\left(-{\frac {\pi }{2}},{\frac {\pi }{2}}\right)$	$C^{\infty }$	כן	לא	כן
Softsign		$f(x)={\frac {x}{1+|x|}}$	$f'(x)={\frac {1}{(1+|x|)^{2}}}$	$(-1,1)$	$C^{1}$	כן	לא	כן
Rectified linear unit ‏(ReLU)		$f(x)={\begin{cases}0&{\text{for }}x<0\\x&{\text{for }}x\geq 0\end{cases}}$	$f'(x)={\begin{cases}0&{\text{for }}x<0\\1&{\text{for }}x\geq 0\end{cases}}$	$[0,\infty )$	$C^{0}$	כן	כן	לא
Parameteric rectified linear unit ‏(PReLU)		$f(\alpha ,x)={\begin{cases}\alpha x&{\text{for }}x<0\\x&{\text{for }}x\geq 0\end{cases}}$	$f'(\alpha ,x)={\begin{cases}\alpha &{\text{for }}x<0\\1&{\text{for }}x\geq 0\end{cases}}$	$(-\infty ,\infty )$	$C^{0}$	כן אם ורק אם $\alpha \geq 0$	כן	כן אם ורק אם $\alpha =1$
Randomized leaky rectified linear unit ‏(RReLU)		$f(\alpha ,x)={\begin{cases}\alpha x&{\text{for }}x<0\\x&{\text{for }}x\geq 0\end{cases}}$	$f'(\alpha ,x)={\begin{cases}\alpha &{\text{for }}x<0\\1&{\text{for }}x\geq 0\end{cases}}$	$(-\infty ,\infty )$	$C^{0}$	כן	כן	לא
Exponential linear unit ‏(ELU)		$f(\alpha ,x)={\begin{cases}\alpha (e^{x}-1)&{\text{for }}x<0\\x&{\text{for }}x\geq 0\end{cases}}$	$f'(\alpha ,x)={\begin{cases}f(\alpha ,x)+\alpha &{\text{for }}x<0\\1&{\text{for }}x\geq 0\end{cases}}$	$(-\alpha ,\infty )$	${\begin{cases}C_{1}&{\text{when }}\alpha =1\\C_{0}&{\text{otherwise }}\end{cases}}$	כן אם ורק אם $\alpha \geq 0$	כן אם ורק אם $0\leq \alpha \leq 1$	כן אם ורק אם $\alpha =1$
Scaled exponential linear unit ‏(SELU)		$f(\alpha ,x)=\lambda {\begin{cases}\alpha (e^{x}-1)&{\text{for }}x<0\\x&{\text{for }}x\geq 0\end{cases}}$ with $\lambda =1.0507$ and $\alpha =1.67326$	$f'(\alpha ,x)=\lambda {\begin{cases}\alpha (e^{x})&{\text{for }}x<0\\1&{\text{for }}x\geq 0\end{cases}}$	$(-\lambda \alpha ,\infty )$	$C^{0}$	כן	לא	לא
SoftPlus		$f(x)=\ln(1+e^{x})$	$f'(x)={\frac {1}{1+e^{-x}}}$	$(0,\infty )$	$C^{\infty }$	כן	כן	לא

הטבלה הבאה מרכזת פונקציות אקטיבציה שאינן פונקציות של משתנה x יחיד מהשכבה או השכבות הקודמות:

שם	משוואה	נגזרת	טווח	פונקציה חלקה
Softmax	$f_{i}({\vec {x}})={\frac {e^{x_{i}}}{\sum _{j=1}^{J}e^{x_{j}}}}$ for i = 1, …, J	${\frac {\partial f_{i}({\vec {x}})}{\partial x_{j}}}=f_{i}({\vec {x}})(\delta _{ij}-f_{j}({\vec {x}}))$	$(0,1)$	$C^{\infty }$
Maxout	$f({\vec {x}})=\max _{i}x_{i}$	${\frac {\partial f}{\partial x_{j}}}={\begin{cases}1&{\text{for }}j={\underset {i}{\operatorname {argmax} }}\,x_{i}\\0&{\text{for }}j\neq {\underset {i}{\operatorname {argmax} }}\,x_{i}\end{cases}}$	$(-\infty ,\infty )$	$C^{0}$

ארכיטקטורות רשת

ארכיטקטורות רשת בולטות כוללות את "המשפחות" שלהלן:

ארכיטקטורה טיפוסית של רשת CNN

Long short-term memory unit

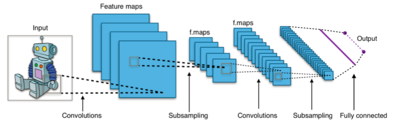
• רשת קונבולוציה – רשתות אלו מתאימות ללמידה של מידע שהוא אינווריאנטי בזמן או במרחב והן מתאימות לעיבוד תמונות.
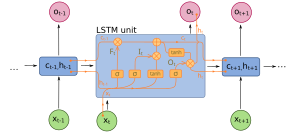
• Recurrent Neural Network – רשתות אלו נועדו "לפענח" מידע סדרתי – כלומר, להביא בחשבון את "סדר ההופעה" של התופעה בה מטפלים. רשתות אלו כוללות מרכיב של זיכרון – כך שהרשת "יודעת להתחשב" בהיסטוריה. רשתות אלו מתאימות במיוחד לקריאת כתב – כאשר יש חשיבות רבה לסדר הופעת האותיות, להפיכת "שמע" לטקסט וכדומה. ז'אנר ספציפי של רשתות אלו הן Bidirectional recurrent neural networks. מכיוון שהרשת מקבלת קטע לפענוח שהוא בעל אורך נתון – היא יכולה להביא בחשבון גם את סדר ההופעה "הרגיל", כלומר, להביא בחשבון את העבר לגבי "מה צפויה" להיות האות הבאה ובמקביל, היא יכולה "להסתכל" על הנתונים גם בכיוון ההפוך (למשל – מסוף המילה אל תחילתה). בנוסף, רשתות אלו מאפשרות להביא בחשבון זמנים (או יחסי קרבה) בעלי אורך משתנה, כלומר, לדוגמה, בהקשר של קריאת כתב, להביא בחשבון הן את האות הקרובה לאות שמנסים לפענח והן אותיות או חלקי מילים רחוקות יותר.
• Autoencoder – רשתות אלו בנויות בארכיטקטורה כזו שגודל השכבות החבויות יורד והולך ואחר כך, הוא גדל חזרה, בדרך כלל, לגודל המקורי, כלומר, רשת בארכיטקטורה הכוללת "צוואר בקבוק". במצב זה, החלק של הרשת מהשכבה של כניסת הנתונים ועד לצוואר בקבוק מהווה "מקודד" של המידע ואילו השכבה מצוואר הבקבוק ועד לשכבת יציאת הנתונים מהווה "מפענח". לרשתות כאלה יש שימושים רבים ולדוגמה, ניתן לאמן את הרשת על תמונות רבות של ואן גוך, מה שיגרום ל"מקודד" "להבין" מה מצויר בתמונה ואילו ה"מפענח" ילמד איך לקחת מידע מקודד שמבטא את "מה מצויר בתמונה" ולהפוך אותו לציור "בסגנון של ואן גוך". רשת כזו, לאחר שאומנה, יכולה לקלוט ציור או צילום אחר כלשהו, "להבין" מה יש בציור ואז "לפתוח מחדש" את המידע המקודד כך שבסופו של התהליך יתקבל הציור/ צילום המקורי – אבל בסגנון של "ואן גוך". שיטה זו מאפשרת להמיר צילומי יום לתמונות שכאילו צולמו בלילה וכדומה.
• Generative adversarial network – רשתות הכוללות שתי ארכיטקטורות נפרדות. רשת אחת מהווה "גנרטור". רשת זו יודעת לייצר בעצמה את הישות שבה מתעניינים – נניח למשל תמונה של פרח. רשת שנייה מהווה "שופט" והיא מנסה להשוות בין התוצרים של ה"גנרטור" לבין תמונות אמיתיות של פרחים. אם השופט מצליח להבין איזה תמונה יוצרה על ידי הגנרטור ואיזה תמונה היא "אמיתית" – משפרים את ה"גנרטור", אם השופט לא מצליח להבחין בין התמונות האמיתיות לבין התמונות שהגנרטור מייצר – משפרים את "השופט" וחוזר חלילה. רשתות כאלה יכולות "לייצר בעצמן" ישויות מגוונות, דומות להפליא למציאות עצמה. נכון ל-2019, הודגמו כבר יכולות לייצר פורטרטים של אנשים לא קיימים, ציפורים, פרחים, קולות וכיוצא באלו. ארכיטקטורה זו פותחה ופורסמה לראשונה על ידי איאן גודפלו בשנת 2014.
• רשת נוירונית מבוססת על מתמיר (Transformer based neural networks) – רשתות נוירונים שהתפתחו בעולם הבנת השפה והן מתאימות במיוחד לטיפול במידע שמגיע כזרם של אלמנטים שונים (לדוגמה מילים במשפט). ברשתות נוירונים מסוג זה אלמנטים מרוחקים בקלט יכולים להשפיע על הפלט ללא איבוד הקשר. רשתות מסוג זה משמשות במודלי שפה גדולים כמו GPT, Bert, ועוד. ליבת המודל היא מציאת ההשפעה של אלמנטים בהיסטוריה על הפלט עבור ערך קלט נוכחי. כיוון שכל אלמנט בקלט משתתף במשפר הקשרים שונים, לדוגמה במשפט "האנשים נעלו את ביתם שבמושבה ונסעו לטיול במכונית" המילה ביתם מתייחסת לעזיבה בהקשר אחד ולמושבה בהקשר אחר", המודל מחשב במקביל מספר הקשרים שונים.

אלגוריתם ללימוד הרשת

מערך השכבות בתצורת "Feed Forward"

הקלטים לנוירון מסוכמים בסכום משוקלל, ואם התוצאה עוברת ערך סף מסוים, הקלט מועבר ליציאה. תצורת הרשת המקובלת ביותר היא זרימה קדימה (Feed Forward) – זאת אומרת, שכבות של נוירונים עם חיבור של כולם עם כולם בין שכבות צמודות. השכבות שבין שכבת הקלט לשכבת הפלט נקראות שכבות חבויות. בהינתן רשת בה כוונו המשקולות, חישוב על ידה מתבצע על ידי הזנת הקלטים לשכבת הקלט וקבלת התוצאה שחלחלה ברשת לשכבת הפלט. מספר נוירונים רב מדי בשכבות החבויות יכול לגרום להתאמת יתר (over-fitting) על סדרת הלימוד. ישנה חשיבות לכך שפונקציית הסף ביציאה מהנוירון תהיה לא ליניארית כדי לפתור בעיות ברמת קושי גבוהה בעזרת הרשת.

הפונקציה אותה מממש כל תא היא פונקציית סיגמואיד (Sigmoid) המתוארת בשרטוט "Sigmoid Unit":

Sigmoid Unit

הביטויים המפורשים הם:

$${\begin{aligned}n_{j}=\mathrm {net} &=\sum _{i}w_{i}x_{i}\\o=\mathrm {output} &=\sigma (\mathrm {net} )\\\sigma (x)&={\frac {1}{1+e^{-x}}}\end{aligned}}$$

הפונקציה $\sigma$ מקיימת תכונה יפה:

$\sigma '(x)={\frac {d\sigma (x)}{dx}}=\sigma (x)\cdot (1-\sigma (x))$.

אם כן, הרשת בה השתמשנו היא רשת בעלת 3 שכבות, בכל שכבה מספר תאים כשכל תא מממש Sigmoid unit.

המשקולות שעל הקשרים בין הנוירונים (המשקולות הסינופטיות) הן אלה שאוגרות את הידע של הרשת במודל המפושט, לכן אלגוריתמי הלימוד השונים מבצעים את כוונון המשקולות לערכים שנותנים תוצאות חישוב טובות עבור מערך דוגמאות הלימוד. משימה זאת אינה פשוטה בגלל השכבות החבויות.

אחד מאלגוריתמי הלימוד המקובלים ביותר הוא אלגוריתם "פעפוע לאחור" (Back-Propagation או BP). זהו אלגוריתם ללימוד מונחה (Supervised Learning). הוא מעביר את קלט הלימוד במורד רשת עם משקולות אקראיות, ומשווה את הפלט המתקבל לפלט הרצוי בכך שהוא מחשב את הטעות עבור כל נוירון פלט.

הרעיון העיקרי של BP הוא שהטעויות מחלחלות חזרה במעלה הרשת כך שמתבצעים כוונוני משקלות בעזרת אלגוריתם Gradient descent, שמנסה להקטין את הטעויות בפלט. אם תיקוני המשקולות נעשים בשיעור מספיק קטן, גדלים הסיכויים להתכנסות של הרשת לטעות מינימלית. אומנם תיתכן התכנסות למינימום מקומי בלבד, אך למעשה השיטה נותנת תוצאות טובות כיוון שניתן להפעילה שוב עם משקולות התחלתיות שונות. אף על פי שהלימוד בשיטה זו דורש משאבים רבים, ובעל זמן ריצה לא זניח, השימוש ברשת אחרי הלימוד הוא מהיר יותר.

אלגוריתם Gradient Descent

ערך מורחב – Gradient descent

את הרשת מאמנים על ידי עדכון המשקולות w_i. הרשת מוזנת בווקטור כניסה מסוים ונבחן מוצאה. בהתאם למוצא הדרוש עבור וקטור כניסה זה מעדכנים את המשקולות. אנו נדון רק באפשרות של עדכון המשקולות על מנת לצמצם את השגיאה הריבועית בין מוצא הרשת למוצא הדרוש. הניסוח המתמטי ל־Gradient Descent הוא:

1. מתחילים עם וקטור משקולות ${\vec {w}}=(w_{i})_{i\in I}$.
2. חשב את השגיאה (או ה"עונש") על ידי $E({\vec {w}})={\frac {1}{2}}\sum _{d}(t_{d}-o_{d})^{2}$ כאשר t_d הוא הערך הרצוי ו־o_d הוא הפלט שבפועל מפיקה הרשת.
3. "אימון הרשת": עדכן את המשקולות
   $$w_{i}\leftarrow w_{i}+\Delta w_{i}$$
   כאשר
   $$.\Delta w_{i}=-\eta {\frac {\partial E}{\partial w_{i}}}$$
   זה למעשה גרדיאנט שכן
   $$.\Delta {\vec {w}}=-\eta {\vec {\nabla }}E({\vec {w}})$$
   ומכאן שם השיטה.

עבור סיגמואיד נקבל

$${\begin{aligned}{\frac {\partial E}{\partial w_{i}}}&={\frac {\partial }{\partial w_{i}}}{\frac {1}{2}}\sum _{d}(t_{d}-o_{d})^{2}={\frac {1}{2}}\sum _{d}{\frac {\partial }{\partial w_{i}}}(t_{d}-o_{d})^{2}\\&={\frac {1}{2}}\sum _{d}2(t_{d}-o_{d}){\frac {\partial }{\partial w_{i}}}(t_{d}-o_{d})=\sum _{d}(t_{d}-o_{d})\left(-{\frac {\partial o_{d}}{\partial w_{i}}}\right)\\&=-\sum _{d}(t_{d}-o_{d}){\frac {\partial o_{d}}{\partial n_{d}}}{\frac {\partial n_{d}}{\partial w_{i}}}\end{aligned}}$$

כאשר $n_{d}=\mathrm {net} _{d}$. אבל אנו יודעים ש־

$${\frac {\partial o_{d}}{\partial n_{d}}}={\frac {\partial \sigma (n_{d})}{\partial n_{d}}}=o_{d}\cdot (1-o_{d})\ ,\quad {\frac {\partial n_{d}}{\partial w_{i}}}={\frac {\partial ({\vec {w}}\cdot {\vec {x}}_{d})}{\partial w_{i}}}=x_{i,d}$$

ולכן

$$.{\frac {\partial E}{\partial w_{i}}}=-\sum _{d}(t_{d}-o_{d})\cdot o_{d}\cdot (1-o_{d})x_{i,d}$$

.

בסך הכל:

$$.w_{i}\leftarrow w_{i}+\eta \sum _{d}(t_{d}-o_{d})\cdot o_{d}\cdot (1-o_{d})x_{i,d}$$

קיבלנו את המשוואה לפיה נעדכן את המשקולות בכל איטרציה כדי להביא למינימום את השגיאה הריבועית במוצא. נשים לב כי כמו בכל שימוש באלגוריתם Gradient Descent אפשר להתכנס למינימום מקומי.

אלגוריתם פעפוע לאחור (Back-Propagation)

בסעיף הקודם קיבלנו את המשוואה לעדכון המשקולות של תא מסוים בהינתן מוצאו והמוצא הדרוש ("מטרה"). עם זאת, במהלך אימון הרשת ידועה לנו רק שכבת היציאה של הרשת כולה (והמטרה שלה), ולא ידועים המוצאים/מטרות של שכבות הביניים. באמצעות אלגוריתם Back-propagation נעדכן את שכבות הביניים גם כן – שכבה אחרי שכבה.

תהליך "אימון" הרשת

תהליך זה הוא הקובע את המשקולות לזיהוי אוטומטי של תבניות ברשת העצבית. להלן דוגמה פשוטה על האופן בו התהליך עשוי להתבצע. דמיינו אלגוריתם הנועד ללמד את הנוירון לעיל לזהות את התבנית המיועדת לו:

1. הצב בהתחלה משקולות רנדומליות בין הנוירונים.
2. אם הפלט נכון, אל תעשה כלום.
3. אם הפלט גבוה אך אמור להיות נמוך, הנמך את המשקולות הקשורות לנתוני הקלט הגבוהים.
4. אם הפלט נמוך אך אמור להיות גבוה, הגבה את המשקולות הקשורות לנתוני הקלט הנמוכים.

כל זאת, כאשר המצב ההתחלתי של ערכי המשקולות אקראי. חלקי המאמר הבאים עוסקים בשיטות שונות לאימון הרשת. יש שתי נקודות נוספות, שכדאי לשים לב אליהן כאן. ראשית, בעזרת קביעת משקולות מתאימה, נוכל ליצור מהרשתות כמעט כל שער לוגי. לכן, אל לנו להתייחס לרשתות העצביות כאמצעי לזיהוי בלבד – הן דבר יותר גמיש מכך. למעשה, הן יותר כמו מעגל לוגי מצרפי הניתן לאימון. שנית, במקום שימוש בפלט בינארי בלבד, כפי שנעשה בכל הדוגמאות בהן עסקנו, נשתמש ככלל בפונקציה המתמטית הנקראת סיגמואיד לפלט הנוירונים שלנו. כלומר הפלט יהיה:

$$o=\mathrm {output} ={\frac {1}{1+e^{-\mathrm {sum} }}}\quad \mathrm {sum} =\sum _{i}w_{i}x_{i}$$

ובכן בדוגמה בשרטוט 5^{[דרושה הבהרה]} פלט הנוירון בשימוש בפונקציית הסיגמואיד יהיה $\mathrm {output} ={\frac {1}{1+e^{-0.18}}}=0.5549$.

איור 12: הנוירון הבינארי ונוירון הסיגמואיד.

למעשה, פונקציה זו מחזירה תמיד מספר בין אפס לאחד, ולכן היא מתנהגת בדומה לפונקציית המדרגה הבינרית, היא בעלת יתרון במקרים בהם קיימות שתי תבניות דומות מאוד. במקרים אלו ניתנת לנוירון בדרך זו האפשרות להחזיר ערך ביניים. זו בעצם דרכו להגיד: "אני לא בטוח". שרטוט 12 מדגים את הרעיון.

תהליך הלמידה מתבצע על ידי "תגמול" "וענישה" של קשרים שונים ועל ידי חשיפת רשת הנוירונים לדוגמאות רבות. "תגמול" ו"ענישה" של הקשרים מתבצע על ידי שינוי המשקל של אותו הקשר, כך שכל קשר ש"מתוגמל" משקלו יגדל וכל קשר ש"נענש" משקלו ירד, תהליך זה משפיע במידה רבה על תהליך העיבוד ברשת הנוירונים ולקבלת תוצאה שונה. כל נוירון בשכבה הראשונה מתעדכן בנתון רלוונטי הנקרא קלט, ולאחר תהליך עיבוד בשכבות הביניים כל נוירון בשכבה האחרונה מיצר פלט הנקרא פתרון. כל אחד מן הנוירונים יכול להשפיע במידה מסוימת על המידע או על תהליך העיבוד שיתבצע בתא אחר בשל הקשרים הקיימים ברשת. פעולת החשיבה נעשית על ידי הזנת נתוני קלט לנוירונים שבשכבה העליונה, והעברת הנתונים בין הנוירונים ובמורד השכבות, עד שנוצר מערך של נתוני פלט בנוירונים שבשכבה התחתונה. נתוני הפלט מהווים מערך של פתרונות הרשת לנתוני הקלט. מדוגמה לדוגמה מתעדכנים "ערכי הסף" של הנוירונים שבמערכת, כך שהפלט יהיה אופטימלי. הערכים המתמטיים של ערכי הסף יכוילו, כך שכל קשר שצריך היה לאשרו יאושר, וכל קשר שצריך היה לדחותו יידחה. מעתה ואילך, אפשר לצפות שהרשת תקבל החלטות לאשר או לדחות באופן שמבטא בצורה מלאה את הניסיון הנצבר בתהליך הלמידה. יכולתה של רשת הנוירונים מושתתת על יכולתה לספק דיוק מקסימלי לכל פונקציה קיימת כאשר דיוק זה יכול להתבצע על ידי הגברת מורכבות הרשת והגדלת מספר השכבות החבויות.

יישומים

דיאגרמת בלוקים של יישום אנלוגי בשרטוט יישום נוירון בחומרה

ניתן ליישם רשתות עצביות בחומרה אנלוגית או דיגיטלית. שלושה מגברים פשוטים נותנים את המשקל לקלט. אם אנו רוצים שהמערכת תלמד בזמן אמת, המגברים צריכים להיות בעלי הגברה דיגיטלית אלקטרונית. הפלט מסוכם, והסַף מופעל על ידי מַשוֶוה (Comparator).

מעגל מסוג זה נבנה בעזרת רכיבים הנקראים מגברי פעולה אנלוגיים (Op Amps) כחלק ממעגל משולב. החיסרון בגישה זו הוא הצורך ברכיבים רבים, אם במערכת נוירונים רבים. בדרך זהה ניתן לייצר מעגלים דיגיטליים: מגברי המשקולות יוחלפו במכפילים דיגיטליים, מגבר הסכום יוחלף בסוֹכֵם, והמשווה יוחלף במפענח, שיעביר אות אם פלט הסוכם יהיה גבוה מערך סף קבוע. בדומה לרשתות האנלוגיות, גם הרשתות הדיגיטליות בזבזניות מבחינת מקום ומשאבים, כיוון שהן נשענות על מכפילים בינאריים, שהם לרוב מעגלים גדולים ומורכבים.

לכן, הדרך הנפוצה ביותר לממש רשת עצבית היא על ידי הדמיה בתוכנה. דרך זו מאפשרת למתכנת לשנות פרמטרים, דוגמת מספר הנוירונים והאופן בו הם מחוברים; פעולה זו יכולה להיעשות בקלות וללא חיווט מחדש שעלותו גבוהה, ובכך מאפשרת הדמיה של חיבור נוירונים רבים בדרך פשוטה. קיימות חבילות תוכנה לכתיבה ואימון של רשתות עצביות, בהן Torch, Theano ו־TensorFlow.

במהלך שנות ה-2000, פותחו יכולות משופרות לתמיכה של חומרה ברשתות עצביות מלאכותיות, ובהן אימון של רשתות עצביות מלאכותיות באמצעות מעבד גרפי. חברת Nvidia פיתחה מגוון מעבדים שתכליתם לתמוך, בעיקר, יישומים של רשתות עצבים מלאכותיות וכך גם אינטל (לדוגמה נרוונה סיסטמס ומובידיוס ) וגוגל (כגון Tensor processing unit ).

מימוש רשת עצבית בתוכנה

מימוש של המודל התאורטי שהוצג לעיל כתוכנת מחשב הוא למעשה אלגוריתם בינה מלאכותית ללמידה חישובית ממשפחת הלמידה המונחית.

בניגוד לפיתוח תוכנה קלאסי, אשר מתמקד במציאת פתרון אלגוריתמי לבעיות, פיתוח בעזרת רשת עצבית מתמקד באימון הרשת, הזנתה במידע מתאים וניתוח הפתרון. משימות אלו הן אמנם מורכבות וקשות לפחות כמו הגישה המסורתית, אך לעיתים קרובות ניתן למצוא בעזרת טכניקה זו פתרונות או קירובים לבעיות קשות.

הדרך הפשוטה היא לאחסן את כל הפרמטרים במערכים: את הקלט והפלט מהרשת ניתן לאחסן במערך אחד ואת המשקולות בשני. לדוגמה, נוכל לאחסן את כל המשקולות במערך תלת־ממדי עם שלושת הפרמטרים הבאים:

[Weights[layer_number, neuron_number, connection_number (מספר שכבה, מספר נוירון, מספר חיבור).

הפלט (כמו גם הקלט) מכל נוירון במערך דו־ממדי עם הפרמטרים הבאים הוא:

[Output[ layer_number, neuron_number (מספר שכבה ומספר נוירון).

אחסון המשקולות ברשת טיפוסית

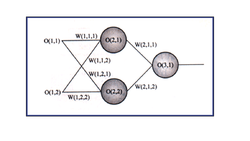
נשים לב כי השדות (O(1,1 ו־(O(1,2 הם קלט הרשת, והשדה (O(3,1 הוא הפלט.

נוכל לגרום למחשב לחשב את הפלט מרשת כזו על ידי אלגוריתם פשוט:

1. אתחל את כל המשקולות ושדות הפלט – השדות O ו־W להיות אפס.
2. קבע את הקלט – שדות (O(1,1 ו־(O(1,2 – לערכים הרצויים כאשר שכבה 1 היא הקלט.
3. קבע את המשקולות הרצויות לרשת.
4. חשב את הפלט מהרשת (בדומה לרשימת "חישוב פלט הרשת").

חישוב פלט הרשת

חבילות תוכנה

לשפת פייתון ישנן מספר חבילות שמממשות רשתות נוירונים מסוגים שונים ומאפשרות שימוש במודולים מוכנים מראש לעיצוב הרשת, אימונה ופרישתה. חבילות אלו כוללות את TensorFlow מבית גוגל ואת Keras שמתלבשת עליה ובעלת API נוח יותר, ואת PyTorch שמשמשת את מטא (פייסבוק וכו').

רשתות עצביות בתעשייה ובאקדמיה

ב־2013 העמידה פייסבוק את מדען המחשב יאן לקון בראש מעבדת הבינה המלאכותית שלה, וב־2014 צירפה למעבדה גם את ולדימיר ופניק. גוגל צירפה אליה במרץ 2013 את ג'פרי הינטון וב־2014 רכשה את DeepMind המתמחה בתחום. אילון מאסק, מייסד חברת טסלה, PayPal ו-SpaceX הקים ב-2015 מיזם לקידום נושאי בינה מלאכותית, בכלל ורשתות עצביות מלאכותיות בפרט בשם OpenAI.

נכון ל-2019 – מינוף עסקי של תחום רשתות העצבים המלאכותיות מתפשט בקצב מאיץ. בתחום פועלות, ככל הנראה, עשרות אלפי חברות ברחבי העולם. ישנן מספר "רשימות" המפרטות את החברות היותר גדולות או יותר מבטיחות בתחום ובכלל זה:

• רשימת החברות בעלות הערך הגבוה (של SingularityHub)
• רשימה של מאה חברות, לפי האתר cbinsights
• רשימה של 25 חברות מובילות, לפי האתר Datamation

אחת הדרכים המקובלות לבחינה ודירוג של האוניברסיטאות בתחום זה, היא הסתכלות על כמות הפרסומים במסגרת הוועדה השנתית שעוסקת בתחום Conference on Neural Information Processing Systems, לפי מדד זה, האוניברסיטאות המובילות בעולם בתחום הן:

• אוניברסיטת קרנגי מלון
• המכון הטכנולוגי של מסצ'וסטס
• אוניברסיטת סטנפורד
• אוניברסיטת קליפורניה בברקלי
• המכון הטכנולוגי של ציריך
• אוניברסיטת טורונטו

רשימה חלקית, על פי דירוג זה, אפשר למצוא ב-Ahead in AI Research? Insights from NIPS

פעילות בישראל

נכון לשנת 2018, לפי דו"ח של מוסד שמואל נאמן למחקר מדיניות לאומית בהמשך למחקר שהוזמן על ידי המועצה הלאומית למחקר ופיתוח אזרחי, בישראל פועלות למעלה מ-800 חברות טכנולוגיות שיש להן פעילות בתחום בינה מלאכותית.

במהלך 2018, ישראל הקימה וועדה שתכליתה לבחון איך נכון למדינה להיערך בתחום הבינה מלאכותית, בראש הוועדה עומדים הפרופסורים יצחק בן ישראל ואביתר מתניה. וועדה זו הקימה 14 וועדות משנה לבחינה של היבטים שונים הקשורים לנושא והיא אמורה להגיש את המלצותיה במהלך 2019. במקביל, הוועדה לתכנון ולתקצוב של האקדמיה, והמועצה להשכלה גבוהה אישרו, כבר במהלך 2018, 16 מסלולי לימוד לתארים אקדמאים בתחום וברוב האוניברסיטאות בישראל, אפשר ללמוד או לחקור היבטים שונים של התחום.

תחומי יישום עיקריים

נכון ל-2019, תחומי היישום העיקריים של רשתות עצבים מלאכותיות כוללים את:

• התחום הפיננסי (לדוגמה – חיזוי של ערך מניה, חיפוש אנומליות לטובת זיהוי זיופים וכיוצא באלו)
• תחום ניהול משאבים של ארגונים גדולים
• פענוח הדמייות רפואיות
• דיאגנוסטיקה רפואית
• אחזור וחיפוש מסמכים
• חיפוש אנומליות רשת לטובת הגנת סייבר
• זיהוי עצמים בתמונות ווידאו
• תחבורה והפחתת עומסי תנועה (באמצעות התאמת פעולת הרמזורים למאפייני התנועה של צומת ספציפי)
• רובוטיקה
• ניתוח נתוני עתק בשוק הקמעונאי, בין השאר לטובת חיזוי והצפת המלצות לצרכנים פוטנציאליים
• כימואינפורמטיקה: חיזוי תכונות של תרכובות כימיות, פיתוח תרופות וחומרים חדשים, תכנון סינתזה כימית

ראו גם

• רשת עצבית
• פרספטרון
• Word2vec

לקריאה נוספת

• Supervised learning in multilayer feedforward networks – "backpropagation", Bruno A. Olshausen, 1998.
• Neural Networks for Pattern Recognition, Bishop, C.M., 1996
• Elektor Electronics 1/2003 C.McLeod and G.Maxwell
• Davies, F., & Moutinho, L., & Curry ,B., (1996). ATM user attitudes: a neural network analysis. Journal of Marketing Intelligence & Planning, 14(2), 26–32.

קישורים חיצוניים

• ישראל בנימיני, גלילאו, בינה מלאכותית: רשתות עצביות נגד פושעים, באתר ynet, 24 במאי 2005
• דן וינר, רשתות בשירות טכנולוגיית החשמל, באתר "סנונית" (הופיע במקור במגזין "כמעט 2000")
• אורי אליאבייב, רשתות נוירונים, Deep learning וכל מה שביניהם, באתר Machine Learning Israel, בתאריך 8 במאי 2016
• רן לוי, למידה עמוקה (Deep Learning) – המחשב והמוח, באתר "עושים היסטוריה" (שידור של הפודקאסט וטקסט מלא שלו)
• רשת עצבית מלאכותית למתחילים – חיזוי תוצאות הטוטו צבי יוליאן רובין
• רשימת סרטונים על רשתות נוירונים מלאכותיות בערוץ 3Blue1Brown ביוטיוב
• רשתות נורליות (מדעי המחשב), דף שער בספרייה הלאומית

הערות שוליים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

39638153רשת עצבית מלאכותית