מכונת וקטורים תומכים

מכונת תמך וקטורי (באנגלית Support Vector Machine, לרוב נכתב ונהגה כראשי-תבות SVM) היא טכניקה של למידה מונחית (supervised learning) המשמשת לניתוח נתונים לסיווג ולרגרסיה.

כנהוג בתחום זה, דוגמאות האימון מיוצגות כווקטורים במרחב ליניארי. עבור בעיות סיווג, בשלב האימון מתאימים מסווג שמפריד נכון ככל האפשר בין דוגמאות אימון חיוביות ושליליות. המסווג שנוצר ב-SVM הוא המפריד הליניארי אשר יוצר מרווח גדול ככל האפשר בינו לבין הדוגמאות הקרובות לו ביותר בשתי הקטגוריות. כאשר מוצגת נקודה חדשה, האלגוריתם יזהה האם היא ממוקמת בתוך הקו המגדיר את הקבוצה, או מחוצה לו.

SVM אינו מוגבל רק לסיווג ליניארי, ויכול לבצע גם סיווג לא ליניארי באמצעות הוספת קרנל (kernel, גרעין) שבו ממופה הקלט למרחב במימד גבוה.

מוטיבציה

סיווג מידע היא פעולה נפוצה בלמידת מכונה. בהינתן אוסף נתונים אשר צריך להפריד אותם לשתי קבוצות על סמך ניסיון קודם (דוגמאות - האם דואר אלקטרוני הוא ספאם או לא; האם מוטציית גן מסוימת מסרטנת או לא; האם כלי רכב כבד הוא טנק או משאית) כאשר המטרה היא להחליט לאיזו משתי הקבוצות לשייך נקודה חדשה. כל נקודה באוסף הנתונים מיוצגת על ידי וקטור בגודל קבוע. בגישה של SVM מחלקים את הנקודות במרחב הווקטורי, באמצעות על-מישור (Hyperplane) כך שהמרווח, המרחק, בין אותו על-מישור המחלק את הנקודות לבין הנקודות הממוקמות הכי קרוב אליו, יהיה המרחק המקסימלי האפשרי.

באופן פורמלי יותר, בהינתן קבוצת אימון של n נקודות מהצורה $({\vec {x_{1}}},y_{1})...({\vec {x_{n}}},y_{n})$ כאשר:

$y_{i}$ הוא $-1$ או $+1$ ומייצג את הקבוצה לה שייכת דוגמה i.
${\vec {x_{i}}}\in \mathbb {R} ^{p}$ הוא וקטור מאפיינים (features, פיצ'רים) המתארים את נקודה i.

ה-SVM בונה על-מישור שהוא המפריד הליניארי (מפריד את המרחב לשני חצאי מרחבים שכל אחד מהם אמור להכיל בעיקר דוגמאות מסוג אחד), וכן שני על-מישורים מקבילים לו, אחד מכל צד, במרחק זהה, אשר מתלכדים עם דוגמת אימון אחת מכל מחלקה. מטרת ה-SVM היא להגדיל את המרחק בין המפריד הליניארי ובין כל אחד מהמישורים המקבילים (מרחק המכונה שוליים), ולמעשה למצוא את המפריד בעל השוליים הרחבים ביותר. דוגמאות האימון המתלכדות עם מישורי השוליים נקראות וקטורים תומכים, ומכאן נגזר שם האלגוריתם.

את העל-מישור ניתן לייצג באמצעות הנקודות ${\vec {x}}$ המקיימות: ${\vec {w}}\cdot {\vec {x}}-b=0$ כאשר ${\vec {w}}$ הוא וקטור נורמלי של העל-מישור (לאו דווקא מנורמל).

הפרדה קשיחה (Hard margin)

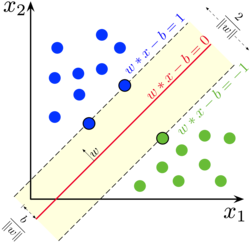
אם ניתן להפריד בצורה ליניארית בין הדוגמאות השייכות לכל קבוצה ניתן למצוא שני על־מישורים שיפרידו ביניהן, כך שהמרחק ביניהם יהיה מרבי. האזור התחום בין שני העל־מישורים קרוי שוליים, והעל מישור בעל השוליים המרביים הוא העל מישור המצוי באמצע ביניהם. את העל־מישור הנ"ל ניתן לייצג באמצעות ${\vec {w}}\cdot {\vec {x}}-b=1$ או ${\vec {w}}\cdot {\vec {x}}-b=-1$ . גאומטרית המרחק בין שני העל־מישורים הנ"ל הוא ${\frac {2}{\|{\vec {w}}\|}}$ , כך שעל מנת למקסם את המרחק מחפשים את ה- $\|{\vec {w}}\|$ המינימלי.

כדי למנוע מדוגמאות האימון להימצא בשוליים המפרידים, מוסיפים את האילוצים הבאים לכל דוגמה $i$ :

${\vec {w}}\cdot {\vec {x_{i}}}-b\geq 1$ אם הדוגמה חיובית,
${\vec {w}}\cdot {\vec {x_{i}}}-b\leq -1$ אם הדוגמה שלילית.

אילוצים אלו מחייבים שכל נקודה תימצא בצד הנכון של המפריד. לחלופין ניתן לכתוב אילוץ זהה המכסה את שני האילוצים:

y_{i}({\vec {w}}\cdot {\vec {x_{i}}}-b)\geq 1

.

הפרדה רכה (Soft margin)

ניתן להרחיב את SVM לטיפול בבעיות שבהן אין הפרדה ליניארית בין שתי הקבוצות באמצעות פונקציית hinge loss:

\max(0,1-y_{i}({\vec {w}}\cdot {\vec {x_{i}}}-b))

הפונקציה הנ"ל מתאפסת כאשר מתקיים התנאי שנדרש בהפרדה קשיחה, כלומר כאשר ${\vec {x_{i}}}$ נמצא בצד הנכון של המפריד. עבור נקודות הנמצאות בצידו הלא נכון של המפריד, מקבלת הפונקציה ערך יחסי למרחב מהמפריד.

בגישה זו ממזערים את הביטוי:

$\left[{\frac {1}{n}}\sum _{i=1}^{n}\max \left(0,1-y_{i}({\vec {w}}\cdot {\vec {x}}_{i}-b)\right)\right]+\lambda \lVert {\vec {w}}\rVert ^{2}$

כאשר $\lambda$ מגדיר את עד כמה מתירים להרחיב את השוליים. עבור $\lambda$ בעל ערך קטן מתנהגת ההפרדה הרכה באופן דומה להפרדה קשיחה כאשר הקלט הוא בר הפרדה ליניארית.

היסטוריה

הבסיס לאלגוריתם למידה חישובית זה הוצג על ידי ולדימיר ופניק ולרנר ב-1963,^[1] ופותח ב-1964 על ידי ופניק ואלכסיי צ'רבוננקיס.^[2] מאז מהווה כלי מרכזי בפתרון בעיות באמצעים סטטיסטיים. ב-1992 בוסלר, גויון וופניק הציגו כיצד ניתן לבנות מסווגים לא ליניאריים באמצעות טריק הקרנל.^[3]

חישוב המסווג

חישוב המסווג נעשה באמצעות הקטנה (מינימיזציה) של הפונקציה:

\left[{\frac {1}{n}}\sum _{i=1}^{n}\max \left(0,1-y_{i}(w\cdot x_{i}+b)\right)\right]+\lambda \lVert w\rVert ^{2}

כאשר 0,1 הם תוצאות השיוך בפועל (מתוך דוגמאות הלמידה), ו-y מייצגת את תוצאת פונקציית הגרעין. בדוגמה זו, y היא פונקציה ליניארית, אולם ניתן להשתמש בפונקציות אחרות, דרך "תעלול הגרעין" (Kernel trick). הפונקציה שאותה ממזערים היא פונקציה קמורה של ${\vec {w}}$ ושל $b$ , שאותה ניתן למזער למשל באמצעות גרדיאנט סטוכסטי (SGD).

קבוע ענישה

אלגוריתם הלמידה מנסה לספק שתי מטרות: סווג נכון של דוגמאות האימון ומיקסום של השוליים. לא אחת המטרות נמצאות בסתירה, ואז יש צורך להגדיר איזו מטרה יותר חשובה. רוב המימושים של SVM מגדירים קבוע ענישה (penalty) על סווג לא נכון (מסומן באות c). ערך c גבוה פירושו העדפת הסיווג הנכון על פני שוליים רחבים, ו c נמוך מעדיף הכללה (שוליים רחבים), גם במחיר שדוגמאות האימון הספציפיות אינן מסווגות נכון.

הפרדה לא ליניארית ותעלול גרעין

בגרסתו הראשון של המודל שהוצגה ב-1963 על ידי ופניק, הגדיר מסווג ליניארי. ב-1992 בוסלר, גויון, וופניק הציגו גישה המאפשרת להשתמש ב-SVM לסיווג לא ליניארי באמצעות שימוש ב"תעלול הגרעין" (Kernel Trick).^[3] מהלך זה מעתיק את דוגמאות האימון מהמרחב הליניארי המקורי למרחב במימד גבוה יותר, מתוך הנחה שבמרחב החדש ימצא מפריד ליניארי טוב יותר מאשר במרחב המקורי. ההעתקה נעשית בעזרת ה"תעלול" - מחליפים את המכפלה הפנימית בה משתמשים עבור המפריד הליניארי, בפונקציית גרעין (kernel function) אשר מדמה את פיזורם מחדש של הווקטורים המקוריים במרחב עשיר יותר, ללא עלות חישובית משמעותית. עם זאת המעבר למימד גבוה עלול לגרום להגדלה של טעות ההכללה.

המפריד הליניארי במרחב הווקטורי החדש הוא מפריד לא ליניארי במרחב המקורי. את מלאכת הסיווג מבצעים אף היא בעזרת אופרטור הגרעין.

פונקציות קרנל נפוצות:

פולינום הומוגני: $k({\vec {x_{i}}},{\vec {x_{j}}})=({\vec {x_{i}}}\cdot {\vec {x_{j}}})^{d}$
פולינום לא הומוגני: $k({\vec {x_{i}}},{\vec {x_{j}}})=({\vec {x_{i}}}\cdot {\vec {x_{j}}}+1)^{d}$
פונקציית בסיס רדיאלי גאוסייני (RBF; radial basis function): $k({\vec {x_{i}}},{\vec {x_{j}}})=\exp(-\gamma \|{\vec {x_{i}}}-{\vec {x_{j}}}\|^{2})$ כאשר $\gamma >0$ . לעיתים מסומן באמצעות $\gamma =1/{2\sigma ^{2}}$ . כך שכיוונון המערכת מתבצע דרך מציאת ערך לקבוע הענישה (C) ול $\sigma$
טנגנס היפרבולי: $k({\vec {x_{i}}},{\vec {x_{j}}})=\tanh(\kappa {\vec {x_{i}}}\cdot {\vec {x_{j}}}+c)$ עבור $\kappa >0$ ו- $c<0$

מימושים נבחרים

ספריית libsvm, תומכת בסיווג ורגרסיה בעזרת סוגים שונים של SVM. הספרייה נכתבה במקור ב C++ וקיימות עבורה תוכנות מעטפת במגוון רב של שפות תכנות ופלטפורמות.
svmlight

הערות שוליים

^ V. N. Vapnik, A. Ya. Lerner, “Recognition of Patterns with help of Generalized Portraits”, Avtomat. i Telemekh., 24:6 (1963), 774–780, www.mathnet.ru
^ History of Support Vector Machines
^ ^3.0 ^3.1 Bernhard E. Boser, Isabelle M. Guyon, Vladimir N. Vapnik, A Training Algorithm for Optimal Margin Classifiers, Proceedings of the Fifth Annual Workshop on Computational Learning Theory, COLT '92, ACM, 1992, עמ' 144–152 doi: 10.1145/130385.130401

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

30655421מכונת וקטורים תומכים

[1] V. N. Vapnik, A. Ya. Lerner, “Recognition of Patterns with help of Generalized Portraits”, Avtomat. i Telemekh., 24:6 (1963), 774–780, www.mathnet.ru

[2] History of Support Vector Machines

[הערה_מספר_20171206064630:0-3] 3.0 ^3.1 Bernhard E. Boser, Isabelle M. Guyon, Vladimir N. Vapnik, A Training Algorithm for Optimal Margin Classifiers, Proceedings of the Fifth Annual Workshop on Computational Learning Theory, COLT '92, ACM, 1992, עמ' 144–152 doi: 10.1145/130385.130401

[1]

[2]

[3]

מכונת וקטורים תומכים

תוכן עניינים