התפלגות בטא

התפלגות בטא

פונקציית צפיפות ההסתברות
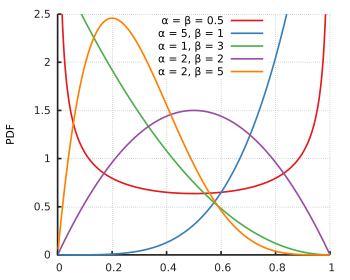פונקציית ההסתברות המצטברת
מאפיינים
פרמטרים	α > 0 β > 0
תומך	$x\in [0,1]$ או $x\in (0,1)$

בתורת ההסתברות ובסטטיסטיקה, התפלגות בטא היא משפחה של התפלגויות רציפות, המוגדרות על הקטע [0,1] ובעלות שני פרמטרים המשפיעים על צורת ההתפלגות: α ו-β. קבוע הנרמול של פונקציית צפיפות ההסתברות הוא פונקציית בטא של הפרמטרים, ומכאן שמה של ההתפלגות.

להתפלגות בטא תפקידים רבים בבחינת התנהגות של משתנים מקריים המוגבלים למרווחים סופיים בדיסציפלינות רבות. הרחבה של ההתפלגות נקראת התפלגות דיריכלה , על שמו של המתמטיקאי הגרמני-צרפתי יוהאן דיריכלה.

מאפיינים

פונקציית הצפיפות

עבור $0\leq x\leq 1$ ועבור הפרמטרים $\alpha ,\beta >0$, פונקציית הצפיפות של ההתפלגות מוגדרת כך:

${\begin{aligned}f(x;\alpha ,\beta )&={\frac {x^{\alpha -1}(1-x)^{\beta -1}}{\displaystyle \int _{0}^{1}u^{\alpha -1}(1-u)^{\beta -1}\,du}}\\[6pt]&={\frac {\Gamma (\alpha +\beta )}{\Gamma (\alpha )\Gamma (\beta )}}\,x^{\alpha -1}(1-x)^{\beta -1}\\[6pt]&={\frac {1}{\mathrm {B} (\alpha ,\beta )}}x^{\alpha -1}(1-x)^{\beta -1}\end{aligned}}$

כאשר $\Gamma (z)$ היא פונקציית גמא ו-B היא פונקציית בטא.

פונקציית הצפיפות המצטברת

פונקציית הצפיפות המצטברת מוגדרת על ידי הנוסחה:

$F(x;\alpha ,\beta )={\dfrac {\mathrm {B} {}(x;\alpha ,\beta )}{\mathrm {B} {}(\alpha ,\beta )}}=I_{x}(\alpha ,\beta )$

כאשר $\mathrm {B} (x;\alpha ,\beta )$ היא פונקציית הבטא הלא שלמה.

התוחלת

התוחלת של ההתפלגות היא פונקציה של היחס β/α:

${\begin{aligned}\mu =\operatorname {E} [X]&=\int _{0}^{1}xf(x;\alpha ,\beta )\,dx\\&=\int _{0}^{1}x\,{\frac {x^{\alpha -1}(1-x)^{\beta -1}}{\mathrm {B} (\alpha ,\beta )}}\,dx\\&={\frac {\alpha }{\alpha +\beta }}\\&={\frac {1}{1+{\frac {\beta }{\alpha }}}}\end{aligned}}$

כאשר הפרמטרים שווים, התוחלת שווה ל-1/2, מה שאומר כי במקרה זה ההתפלגות היא סימטרית והתוחלת היא מרכז התפלגות.

השונות

השונות של ההתפלגות מוגדרת כך:

$\operatorname {var} (X)=\operatorname {E} [(X-\mu )^{2}]={\frac {\alpha \beta }{(\alpha +\beta )^{2}(\alpha +\beta +1)}}$

כאשר $\alpha =\beta$, השונות היא:

$\operatorname {var} (X)={\frac {1}{4(2\alpha +1)}},$

קישורים חיצוניים

מדיה וקבצים בנושא התפלגות בטא בוויקישיתוף

• התפלגות בטא, באתר MathWorld (באנגלית)

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

התפלגות בטא32778802Q756254