התפלגות דיריכלה
| פונקציית צפיפות ההסתברות | |
 | |
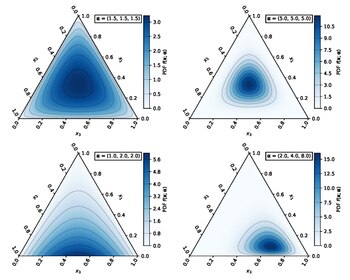| מאפיינים | |
|---|---|
| פרמטרים |
$ K\geq 2 $ מספר הקטגוריות (מספר שלם) $ {\boldsymbol {\alpha }}=(\alpha _{1},\ldots ,\alpha _{K}) $ פרמטרים של ריכוז, כאשר $ \alpha _{i}>0 $ |
| תומך | $ x_{1},\ldots ,x_{K} $ where $ x_{i}\in [0,1] $ and $ \sum _{i=1}^{K}x_{i}=1 $ |
|
פונקציית צפיפות הסתברות (pdf) |
$ {\frac {1}{\mathrm {B} ({\boldsymbol {\alpha }})}}\prod _{i=1}^{K}x_{i}^{\alpha _{i}-1} $ where $ \mathrm {B} ({\boldsymbol {\alpha }})={\frac {\prod _{i=1}^{K}\Gamma (\alpha _{i})}{\Gamma {\bigl (}\alpha _{0}{\bigr )}}} $ where $ \alpha _{0}=\sum _{i=1}^{K}\alpha _{i} $ |
| תוחלת |
=$ \operatorname {E} [X_{i}]={\frac {\alpha _{i}}{\alpha _{0}}} $ $ \operatorname {E} [\ln X_{i}]=\psi (\alpha _{i})-\psi (\alpha _{0}) $ (כאשר $ \psi $ היא פונקציית דיגמה) |
| ערך שכיח | $ x_{i}={\frac {\alpha _{i}-1}{\alpha _{0}-K}},\quad \alpha _{i}>1. $ |
| שונות |
$ \operatorname {Var} [X_{i}]={\frac {{\tilde {\alpha }}_{i}(1-{\tilde {\alpha }}_{i})}{\alpha _{0}+1}}, $ $ \operatorname {Cov} [X_{i},X_{j}]={\frac {\delta _{ij}\,{\tilde {\alpha }}_{i}-{\tilde {\alpha }}_{i}{\tilde {\alpha }}_{j}}{\alpha _{0}+1}} $ כאשר $ {\tilde {\alpha }}_{i}={\frac {\alpha _{i}}{\alpha _{0}}} $, ו- $ \delta _{ij} $ היא הדלתא של קרונקר |
| אנטרופיה |
$ H(X)=\log \mathrm {B} ({\boldsymbol {\alpha }}) $$ +(\alpha _{0}-K)\psi (\alpha _{0})- $$ \sum _{j=1}^{K}(\alpha _{j}-1)\psi (\alpha _{j}) $ כאשר $ \alpha _{0} $ מוגדר כמו בשונות, למעלה; ו- $ \psi $ היא פונקציית דיגמה |
|
פונקציה יוצרת מומנטים (mgf) | $ \alpha _{i}=E[X_{i}]\left({\frac {E[X_{j}](1-E[X_{j}])}{V[X_{j}]}}-1\right) $ where $ j $ is any index, possibly $ i $ itself |
בתורת ההסתברות ובסטטיסטיקה, התפלגות דיריכלה (על שם Peter Gustav Lejeune Dirichlet ), מסומנת לעיתים קרובות $ \operatorname {Dir} ({\boldsymbol {\alpha }}) $, היא משפחה של התפלגויות רב-משתניות רציפות המוגדרות על ידי וקטור $ {\boldsymbol {\alpha }} $ של ממשיים חיוביים. זוהי הכללה רב-משתנית של התפלגות ביתא,[1] ומכאן שמה החלופי - התפלגות בטא רב-משתנית (MBD). [2] התפלגות Dirichlet משמשת בדרך כלל כהתפלגות פריורית בסטטיסטיקה בייסיאנית, ולמעשה, התפלגות Dirichlet היא ההתפלגות הצמודה של ההתפלגות הקטגוריאלית וההתפלגות המולטינומית.
ההכללה האינסוף-ממדית של התפלגות דיריכלה היא תהליך דיריכלה.
הגדרות
פונקציית צפיפות הצפיפות
להתפלגות דיריכלה מסדר $ K\geq 2 $ עם פרמטרים $ 0<\alpha _{1},...\alpha _{K} $, יש פונקציית צפיפות, לפי למידת לבג במרחב האוקלידי $ \mathbb {R} ^{K-1} $, המתוארת באמצעות:
- $ f\left(x_{1},\ldots ,x_{K};\alpha _{1},\ldots ,\alpha _{K}\right)={\frac {1}{\mathrm {B} ({\boldsymbol {\alpha }})}}\prod _{i=1}^{K}x_{i}^{\alpha _{i}-1} $
- כאשר $ \{x_{k}\}_{k=1}^{k=K} $ שייכים לסימפלקס $ K-1 $ תקני, או באופן שקול, לכל $ {\textstyle i\in \{1,\dots ,K\}} $, $ {\textstyle \sum _{i=1}^{K}x_{i}=1{\mbox{, }}x_{i}\in \left[0,1\right]} $.
הקבוע המנרמל הוא פונקציית בטא רב-משתנית, שניתן לבטאו במונחים של פונקציית גמא :
- $ \mathrm {B} ({\boldsymbol {\alpha }})={\frac {\prod \limits _{i=1}^{K}\Gamma (\alpha _{i})}{\Gamma \left(\sum \limits _{i=1}^{K}\alpha _{i}\right)}},\qquad {\boldsymbol {\alpha }}=(\alpha _{1},\ldots ,\alpha _{K}) $
קישורים חיצוניים
הערות שוליים
- ↑ S. Kotz; N. Balakrishnan; N. L. Johnson (2000). Continuous Multivariate Distributions. Volume 1: Models and Applications. New York: Wiley. ISBN 978-0-471-18387-7. (Chapter 49: Dirichlet and Inverted Dirichlet Distributions)
- ↑ Olkin, Ingram; Rubin, Herman (1964). "Multivariate Beta Distributions and Independence Properties of the Wishart Distribution". The Annals of Mathematical Statistics. 35 (1): 261–269. doi:10.1214/aoms/1177703748. JSTOR 2238036.
התפלגות דיריכלה38156061Q981016