MISTY (צופן)

MISTY היא משפחה של צפני בלוקים שפותחו על ידי מיצורו מצואי (Mitsuru Matsui) ועמיתיו מתאגיד מיצובישי יפן. הגרסה הראשונה MISTY פותחה ב-1996 והוצעה לפרויקט NESSIE האירופאי ונכללה בשנת 2003 ברשימה המומלצת של הפרויקט. גרסה אחרת של הצופן הנקראת KASUMI פותחה ב-1999 במיוחד עבור תקן 3GPP לתקשורת סלולרית מסוג GSM, GPRS והדור השלישי UMTS להגנה על פרטיות ואימות שיחה סלולרית.

MISTY הוא צופן בלוקים בסגנון רשת פייסטל רקורסיבית המותאם במיוחד לחומרה. הקלט שלו הוא בלוק טקסט קריא באורך 64 סיביות ומפתח סודי באורך 128 סיביות והפלט הוא טקסט מוצפן באורך 64 סיביות. מספר הסבבים בהגדרה יכול להשתנות, אך מקובל בדרך כלל שמונה סבבים. הבסיס התאורטי של הצופן נשען על נוסחה מתמטית המאפשרת הוכחת עמידות נגד קריפטואנליזה דיפרנציאלית וליניארית. ברמה העליונה הצופן כולל שמונה סבבים של פונקציה אי-ליניארית בולאנית שהיא עצמה מורכבת מ"סולם" דמוי רשת פייסטל בשלושה סבבים של פונקציה פנימית אחרת (כמתואר בתרשימים). באותו סגנון הפונקציה הפנימית בתורה מורכבת גם היא ממספר סבבים של החלפה תוך שימוש בשתי תיבות החלפה S7 ו-S9 המורכבות מטבלה של $7\times 7$ סיביות וטבלה של $9\times 9$ סיביות בהתאמה.

שם הצופן יכול להתפרש כראשי התיבות "Mitsubishi Improved Security TechnologY" או האותיות הראשונות של שמות צוות הפיתוח Matsui Mitsuru, Ichikawa Tetsuya, Sorimachi Toru, Tokita Toshio, Yamagishi Atsuhiro.

גרסאות

תרשים סכמטי של צופן MISTY-1 וצופן MISTY-2. ההבדל ביניהם שהימני מאפשר הפעלה מקבילית ולכן ביישום ממוטב יכול להיות מהיר פי שניים מהשמאלי.

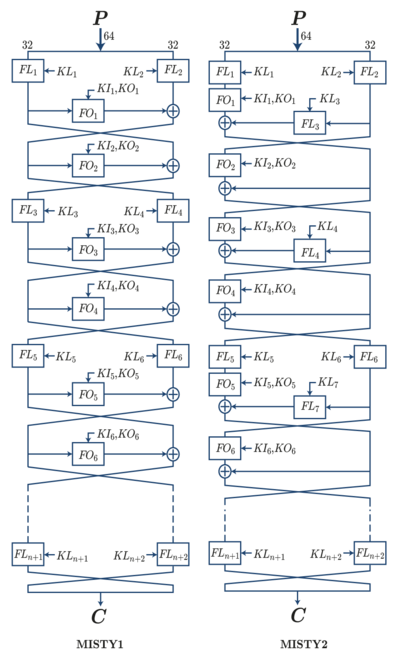
בתחילה פותחו הגרסאות MISTY1 ו-MISTY2 שההבדל ביניהן הוא בעיקר ש-MISTY2 מאפשרת הפעלה מקבילית של הפונקציה הפנימית בעוד ש-MISTY1 איננה מקבילית. ב-2005 פותחה הגרסה KASUMI שהיא חלק מ-A5/3, תקן תקשורת מאובטחת לרשתות סלולריות מהדור השלישי שמחליף את האלגוריתמים A5/1 ו-A5/2. ב-1998 פורסם צופן E2 שהיה מועמד ל-AES ובשנת 2000 פותח על בסיס דומה צופן קמליה שנחשב לבטוח ברמה של AES ונכלל בתקנים רבים וב-SSL.

ערכי תיבות ההחלפה שונים בגרסאות השונות. המפתח הסודי לאחר הרחבה מעורבב עם הקלט בשלבים שונים של הצופן. ב-MISTY1, KASUMI וקמליה קיימת פונקציה נוספת שתפקידה להוסיף טרנספורמציה ליניארית תלוית מפתח. שכבות הפונקציה הליניארית מפרידות כל זוג סבבים של הצופן, למשל ב-KASUMI הפונקציה הליניארית נוספת לפני הפונקציה הפנימית בסבב אי-זוגי ואחריה בסבב זוגי. הבדל נוסף קיים בפונקציית הרחבת המפתח, כאשר ב-MISTY1 ו-MISTY2 היא כוללת טרנספורמציה אי-ליניארית. לעומת זאת מסיבות של יעילות ב-KASUMI פונקציית הרחבת המפתח ליניארית לחלוטין, מה שמהווה נקודת תורפה.

כל הגרסאות של הצופן רשומות כפטנט על ידי NTT ומיצובישי אלקטרוניקה, חלקן הותרו לשימוש תחת רישיונות FreeBSD או לשימוש אקדמי/שלא למטרות רווח.

בטחון

לפי הצהרת מיצואי, הצופן הוכח בטוח נגד התקפה דיפרנציאלית/ליניארית וכן נגד התקפות מודרניות נוספות. בשמונה סבבים הסיבוכיות הדיפרנציאלית והליניארית שלו הן בסדר גודל של $2^{-140}$ בהשוואה ל-DES שהן $2^{-62}$ ו-$2^{-46}$ בהתאמה. MISTY1 נחקר במשך שנים רבות מאז הוצע לראשונה ולא נמצאו בו פגמים רציניים. ההתקפה הטובה יותר הידועה היא "התקפה אינטגרלית" של קנודסן ווגנר מ-2002 נגד גרסה מצומצמת של הצופן בחמשה סבבים, בסיבוכיות של $2^{48}$ ובסיבוכיות מקום של $2^{34}$. אותה התקפה נגד MISTY2 בשישה סבבים אפשרית בסיבוכיות של $2^{71}$ ומקום בסדר גודל של $2^{34}$. נגד KASUMI התגלו מספר התקפות חלקן תאורטיות כלומר בסיבוכיות טובה מכוח גס ($2^{100}$ עם $2^{28}$) וחלקן מעשיות כמו ההתקפת Related-key של אור דונקלמן, נתן קלר ועדי שמיר משנת 2010 שהיא בסיבוכיות של $2^{32}$ ומקום בסדר גודל של $2^{30}$ עם 4 מפתחות קשורים. ראוי לציין שההתקפה האחרונה אינה ישימה נגד MISTY1, כמו כן היא מסתמכת על כמות נכבדה של טקסט מוצפן בשילוב עם מפתחות קשורים, לכן ייתכן שהיא אינה אפשרית נגד יישום A5/3 בגרסה הנוכחית, אך יש להביא בחשבון את האיום. על כל פנים ההתקפה מוכיחה שהשינויים שנעשו על ידי המפתחים במעבר מ-MISTY ל-KASUMI כדי לשפר ביצועים בחומרה למעשה החלישו את בטחון הצופן משמעותית. מסיבה זו הוחלט על מעבר לצופן חזק יותר SNOW 3G.

תיאור הצופן

בפיתוח הצופן הושם דגש בעיקר על יישום יעיל, במיוחד בחומרה. הפעולות הנפוצות בצופן בלוקים מתחלקות לארבע קטגוריות עיקריות; פעולות אריתמטיות, פעולות הזזה (Shift), פעולות לוגיות (כמו XOR) וטבלאות החלפה (S-box). מתוכן שתי הפעולות האחרונות עדיפות מהיבט של חומרה ולכן נבחרו. האסטרטגיה הבסיסית בפיתוח הצופן הייתה בנייה מלמטה למעלה, מהמרכיבים הקטנים לגדולים בצורה רקורסיבית, כך שיהיה קל להעריך את בטחון ההצפנה במונחים של הסתברות דיפרנציאלית/ליניארית.

כמו ברשת פייסטל טיפוסית, הקלט $P$ באורך 64 סיביות מחולק לשני חצאים בגודל 32 סיביות כל אחד והפונקציה הפנימית מופעלת על המחצית האחת והפלט שלה משמש כמפתח הצפנה להצפנת המחצית השנייה, תוך שימוש בפעולות XOR ועם שתי תת-שגרות $FO$ ו-$FL$. פלט הצופן $C$ הוא באורך 64 סיביות. בפונקציה $FO$ מחלקים את הקלט שוב לשני חצאים באורך 16 סיביות, כל אחד מהווה קלט לפונקציה קטנה יותר הנקראת $FI$ המשתמשת בתיבות ההחלפה (להלן), היות ש-16 סיביות הן ערן גדול מדי, מחלקים שוב את הקלט הפעם לשני חלקים לא שווים, 9 סיביות ו-7 סיביות בהתאמה אותם מחליפים לפי תיבות ההחלפה בהתאמה. הסיבה לחלוקה לא מאוזנת זו נובעת מהעובדה שתיבות החלפה המייצגות פונקציה חד-חד-ערכית ועל אי ליניארית, טובות יותר באורך אי זוגי מהיבט של קריפטונאליזה דיפרנציאלית/ ליניארית, אולם מאידך חסרונן הוא בהפחתה ביעילות יישום הן בחומרה והן בתוכנה. לפי בדיקות שנעשו על מחשב פנטיום מהירות ההצפנה הייתה 20Mbps בקירוב, על חומרה המהירויות הן 450Mbps בקירוב. מבנה MISTY2 מאפשר הפעלה מקבילית ולכן מהיר פי שניים בהצפנה, אך לא בפענוח כי הפונקציה ההופכית לא ניתנת להפעלה מקבילית, מסיבה זו MISTY2 עדיף ליישום במצבי הפעלה OFB או CFB הפועלים כצופן זרם בהם נדרשת רק פונקציית ההצפנה.

תיבות החלפה

תיבות ההחלפה הן למעשה חזקות מעל שדה סופי. התיבות חושבו כך שההסתברות הדיפרנציאלית/ליניארית הממוצעת תהיה מינימלית וכן שיהיו ממעלה גבוהה ככל האפשר ושיהיה להן עיכוב מינימלי בביצוע בחומרה. החיפוש התמקד בפונקציות ליניאריות מהצורה $S_{i}(x)=A\circ x^{\alpha }\ (i=7,9)$. הטבלה S7 כוללת אוסף של 7 פונקציות ממעלה 10 מהצורה $A\circ x^{\alpha }$ מעל השדה $GF(2^{7})$ בבסיס פולינומי, כאשר ${\text{GCD}}(2^{7}-1,\alpha )=1$. באותה דרך הטבלה S9 כוללת אוסף של 9 פונקציות ממעלה לכל היותר 13 מעל השדה $GF(2^{9})$. אפשר להפעיל את ההחלפה ישירות באמצעות הפונקציות האמורות ללא שימוש בזיכרון (כאשר החומרה מוגבלת משאבים) או שאפשר להמירן לטבלאות חיפוש אם הזיכרון זמין. להלן הטבלאות S7 ו-S9:

S7

0 1 2 3 4 5 6 7 8 9 a b c d e f 00: 1b 32 33 5a 3b 10 17 54 5b 1a 72 73 6b 2c 66 49 10: 1f 24 13 6c 37 2e 3f 4a 5d 0f 40 56 25 51 1c 04 20: 0b 46 20 0d 7b 35 44 42 2b 1e 41 14 4b 79 15 6f 30: 0e 55 09 36 74 0c 67 53 28 0a 7e 38 02 07 60 29 40: 19 12 65 2f 30 39 08 68 5f 78 2a 4c 64 45 75 3d 50: 59 48 03 57 7c 4f 62 3c 1d 21 5e 27 6a 70 4d 3a 60: 01 6d 6e 63 18 77 23 05 26 76 00 31 2d 7a 7f 61 70: 50 22 11 06 47 16 52 4e 71 3e 69 43 34 5c 58 7d

S9

0 1 2 3 4 5 6 7 8 9 a b c d e f 000: 1c3 0cb 153 19f 1e3 0e9 0fb 035 181 0b9 117 1eb 133 009 02d 0d3 010: 0c7 14a 037 07e 0eb 164 193 1d8 0a3 11e 055 02c 01d 1a2 163 118 020: 14b 152 1d2 00f 02b 030 13a 0e5 111 138 18e 063 0e3 0c8 1f4 01b 030: 001 09d 0f8 1a0 16d 1f3 01c 146 07d 0d1 082 1ea 183 12d 0f4 19e 040: 1d3 0dd 1e2 128 1e0 0ec 059 091 011 12f 026 0dc 0b0 18c 10f 1f7 050: 0e7 16c 0b6 0f9 0d8 151 101 14c 103 0b8 154 12b 1ae 017 071 00c 060: 047 058 07f 1a4 134 129 084 15d 19d 1b2 1a3 048 07c 051 1ca 023 070: 13d 1a7 165 03b 042 0da 192 0ce 0c1 06b 09f 1f1 12c 184 0fa 196 080: 1e1 169 17d 031 180 10a 094 1da 186 13e 11c 060 175 1cf 067 119 090: 065 068 099 150 008 007 17c 0b7 024 019 0de 127 0db 0e4 1a9 052 0a0: 109 090 19c 1c1 028 1b3 135 16a 176 0df 1e5 188 0c5 16e 1de 1b1 0b0: 0c3 1df 036 0ee 1ee 0f0 093 049 09a 1b6 069 081 125 00b 05e 0b4 0c0: 149 1c7 174 03e 13b 1b7 08e 1c6 0ae 010 095 1ef 04e 0f2 1fd 085 0d0: 0fd 0f6 0a0 16f 083 08a 156 09b 13c 107 167 098 1d0 1e9 003 1fe 0e0: 0bd 122 089 0d2 18f 012 033 06a 142 0ed 170 11b 0e2 14f 158 131 0f0: 147 05d 113 1cd 079 161 1a5 179 09e 1b4 0cc 022 132 01a 0e8 004 100: 187 1ed 197 039 1bf 1d7 027 18b 0c6 09c 0d0 14e 06c 034 1f2 06e 110: 0ca 025 0ba 191 0fe 013 106 02f 1ad 172 1db 0c0 10b 1d6 0f5 1ec 120: 10d 076 114 1ab 075 10c 1e4 159 054 11f 04b 0c4 1be 0f7 029 0a4 130: 00e 1f0 077 04d 17a 086 08b 0b3 171 0bf 10e 104 097 15b 160 168 140: 0d7 0bb 066 1ce 0fc 092 1c5 06f 016 04a 0a1 139 0af 0f1 190 00a 150: 1aa 143 17b 056 18d 166 0d4 1fb 14d 194 19a 087 1f8 123 0a7 1b8 160: 141 03c 1f9 140 02a 155 11a 1a1 198 0d5 126 1af 061 12e 157 1dc 170: 072 18a 0aa 096 115 0ef 045 07b 08d 145 053 05f 178 0b2 02e 020 180: 1d5 03f 1c9 1e7 1ac 044 038 014 0b1 16b 0ab 0b5 05a 182 1c8 1d4 190: 018 177 064 0cf 06d 100 199 130 15a 005 120 1bb 1bd 0e0 04f 0d6 1a0: 13f 1c4 12a 015 006 0ff 19b 0a6 043 088 050 15f 1e8 121 073 17e 1b0: 0bc 0c2 0c9 173 189 1f5 074 1cc 1e6 1a8 195 01f 041 00d 1ba 032 1c0: 03d 1d1 080 0a8 057 1b9 162 148 0d9 105 062 07a 021 1ff 112 108 1d0: 1c0 0a9 11d 1b0 1a6 0cd 0f3 05c 102 05b 1d9 144 1f6 0ad 0a5 03a 1e0: 1cb 136 17f 046 0e1 01e 1dd 0e6 137 1fa 185 08c 08f 040 1b5 0be 1f0: 078 000 0ac 110 15e 124 002 1bc 0a2 0ea 070 1fc 116 15c 04c 1c2

הכנת מפתח

בהינתן המפתח הסודי המסופק על ידי המשתמש באורך 128 סיביות, מרחיבים אותו ל-256 סיביות באמצעות הזזה מעגלית וחיבור XOR עם פונקציה ליניארית. השימוש בו הוא באופן שכל סבב מושפע מכל סיביות המפתח ומחלק גדול של המפתח המורחב. ההגבלה ל-256 סיביות נובעת בשל הצורך בהתחשבות בחומרה מוגבלת משאבים כמו כרטיס חכם. הרחבת המפתח נעשית באופן הבא:

${\text{For }}i=0{\text{ to }}7{\text{ do: }}$

$EK[i]=K[i\cdot 2]\cdot 256+K[i\cdot 2+1]$

${\text{For }}i=0{\text{ to }}7{\text{ do: }}$

$EK[i+8]=\mathbf {FI} (EK[i],EK[(i+1){\text{ mod }}8]$

$EK[i+16]=EK[i+8]\land {\text{0x1FF}}$

$EK[i+24]=EK[i+8]\gg 9$

תהליך הרחבת המפתח של MISTY

‏

הצפנה ופענוח

הפונקציה FO מקבלת שני פרמטרים, קלט באורך 32 סיביות FO_IN ואינדקס $k$ לחלק המתאים במפתח המורחב EK ומחזירה את FO_OUT כדלהלן:

$\mathbf {FO} (\mathbf {FO\_IN} ,\mathbf {k} )$

$t_{0}=FO\_IN\gg 16$

$t_{1}=FO\_IN\land {\text{0xFFFF}}$

$t_{0}=t_{0}\oplus EK[k]$

$t_{0}=\mathbf {FI} (t_{0},EK[(k+5){\text{ mod }}8+8])$

$t_{0}=t_{0}\oplus t_{1}$

$t_{1}=t_{1}\oplus EK[(k+2){\text{ mod }}8]$

$t_{1}=\mathbf {FI} (t_{1},EK[(k+1){\text{ mod }}8+8])$

$t_{1}=t_{1}\oplus t_{0}$

$t_{0}=t_{0}\oplus EK[(k+7){\text{ mod }}8]$

$t_{0}=\mathbf {FI} (t_{0},EK[(k+3){\text{ mod }}8+8])$

$t_{0}=t_{0}\oplus t_{1}$

$t_{1}=t_{1}\oplus EK[(k+4){\text{ mod }}8]$

$FO\_OUT=(t_{1}\ll 16)\lor t_{0}$

${\text{Return }}FO\_OUT$

הפונקציות הפנימיות של MISTY

‏

‏

‏

הפונקציה FI מקבלת שני פרמטרים; קלט באורך 16 סיביות F_IN וחלק מהמפתח המורחב FI_KEY ומחזירה פלט באורך 16 סיביות FI_OUT. הפונקציה משתמשת בשני משתני עזר מקומיים d_7 באורך 7 סיביות ו-d_9 באורך 9 סיביות וכן מנצלת את תיבות ההחלפה המתוארות לעיל. בגלל האורך השונה של המשתנים d_7 ו-d_9 יש צורך להפעיל פונקציה כלשהי שמרחיבה או מכווצת את המשתנה בהתאם לפני שמבצעים XOR. הרחבה נעשית על ידי הוספת שני אפסים משמאל (בצד המשמעותי של המספר) וכיווץ נעשה על ידי חיתוך שתי הסיביות המשמעותיות.

$\mathbf {FI} (\mathbf {FI\_IN,FI\_KEY} )$

$d_{9}=FI\_IN\gg 7$

$d_{7}=FI\_IN\land {\text{0x7F}}$

$d_{9}={\text{S9TABLE}}[d_{9}]\oplus d_{7}$

$d_{7}={\text{S7TABLE}}[d_{7}]\oplus d_{9}$

$(d_{7}=d_{7}\land {\text{0x7F}})$

$d_{7}=d_{7}\oplus (FI\_KEY\gg 9)$

$d_{9}=d_{9}\oplus (FI\_KEY\land {\text{0x1FF}})$

$d_{9}={\text{S9TABLE}}[d_{9}]\oplus d_{7}$

$FI\_OUT=(d_{7}\ll 9)\lor d_{9}$

${\text{Return }}FI\_OUT$

הפונקציה FL מקבלת שני פרמטרים; קלט באורך 32 סיביות FL_IN ואינדקס k לחלק המתאים במפתח המורחב ומחזירה את FL_OUT באורך 32 סיביות.

$\mathbf {FL} (\mathbf {FL\_IN,k} )$

$d_{0}=FL\_IN\gg 16$

$d_{1}=FL\_IN\land {\text{0xFFFF}}$

${\text{If k is even then: }}$

$d_{1}=d_{1}\oplus (d_{0}\land EK[k/2])$

$d_{0}=d_{0}\oplus (d_{1}\lor EK[(k/2+6){\text{ mod }}8+8])$

${\text{Else}}$

$d_{1}=d_{1}\oplus (d_{0}\land EK[((k-1)/2+2){\text{ mod }}8+8])$

$d_{0}=d_{0}\oplus (d_{1}\lor EK[((k-1)/2+4){\text{ mod }}8])$

$FL\_OUT=(d_{0}\ll 16)\lor d_{1}$

${\text{Return }}FL\_OUT$

במצבי הפעלה ECB ו-CBC בפענוח צריך להשתמש בפונקציה ההופכית FLINV הבאה:

$\mathbf {FLINV} (\mathbf {FL\_IN,k} )$

$d_{0}=FL\_IN\gg 16$

$d_{1}=FL\_IN\land {\text{0xFFFF}}$

${\text{If k is even then: }}$

$d_{0}=d_{0}\oplus (d_{1}\lor EK[(k/2+6){\text{ mod }}8+8])$

$d_{1}=d_{1}\oplus (d_{0}\land EK[k/2])$

${\text{Else}}$

$d_{0}=d_{0}\oplus (d_{1}\lor EK[((k-1)/2+4){\text{ mod }}8])$

$d_{1}=d_{1}\oplus (d_{0}\land EK[((k-1)/2+2){\text{ mod }}8+8])$

$FL\_OUT=(d_{0}\ll 16)\lor d_{1}$

${\text{Return }}FL\_OUT$

באופן רגיל התהליך האמור מבוצע שמונה פעמים. בכל סבב מתבצעת הקריאה לפונקציה FO. בנוסף בכל סבב זוגי מתבצעת קריאה לפונקציה FL. לאחר הסבב האחרון מתבצעת קריאה נוספת לפונקציה FL. לצורך המחשה אם הקלט חולק לשני חצאים R ו-L בהתאמה, שמונה הסבבים של הצופן נראים כך:

הצפנה	פענוח
R = P & 0xffffffff L = P >> 32 // 1. R = FL(R, 0) L = FL(L, 1) L = L ^ FO(R, 0) 2. R = R ^ FO(L, 1) 3. R = FL(R, 2) L = FL(L, 3) L = L ^ FO(R, 2) 4. R = R ^ FO(L, 3) 5. R = FL(R, 4) L = FL(L, 5) L = L ^ FO(R, 4) 6. R = R ^ FO(L, 5) 7. R = FL(R, 6) L = FL(L, 7) L = L ^ FO(R, 6) 8. R = R ^ FO(L, 7) R = FL(R, 8) L = FL(L, 9) C = (R << 32) | L	R = C & 0xffffffff L = C >> 32 // R = FLINV(R, 8) L = FLINV(L, 9) R = R ^ FO(L, 7) L = L ^ FO(R, 6) R = FLINV(R, 6) L = FLINV(L, 7) R = R ^ FO(L, 5) L = L ^ FO(R, 4) R = FLINV(R, 4) L = FLINV(L, 5) R = R ^ FO(L, 3) L = L ^ FO(R, 2) R = FLINV(R, 2) L = FLINV(L, 3) R = R ^ FO(L, 1) L = L ^ FO(R, 0) R = FLINV(R, 0) L = FLINV(L, 1) P = (R << 32) | L

ראו גם

• צופן בלוקים
• GSM
• KASUMI

הערות שוליים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0