אלגוריתם פוליג-הלמן

שיטת פוליג הלמן

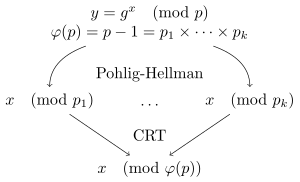
בתורת החבורות ובקריפטוגרפיה אלגוריתם פוליג-הלמן (באנגלית: Pohlig–Hellman algorithm) הוא אלגוריתם לפתרון בעיית הלוגריתם הבדיד במקרה הפרטי כאשר סדר החבורה הוא מספר חלק (שגורמיו הראשוניים קטנים). האלגוריתם הומצא ב-1978 על ידי סטיבן פוליג ומרטין הלמן.

בעיית הלוגריתם הבדיד

ערך מורחב – בעיית הלוגריתם הבדיד

בעיית הלוגריתם הבדיד נחשבת במקרה הכללי לבעיה קשה. האלגוריתם הטוב ביותר הידוע לפתרון הבעיה כאשר סדר החבורה הוא מספר ראשוני הוא אלגוריתם רו של פולרד המבוסס על אלגוריתם צעד-קטן צעד-גדול.

בעיית הלוגריתם הבדיד הכללית היא: בהינתן חבורה ציקלית $\mathbb {G}$ מסדר $q$ ויוצר $g$ ויהי $h\in \mathbb {G}$ איבר כלשהו. מצא $x$ המקיים $h=g^{x}$. הוא נקרא הלוגריתם הבדיד של $h$ בבסיס $g$ בקיצור $\log _{g}h$. אם $q$ ראשוני, אלגוריתם צעד-קטן צעד-גדול פותר את הבעיה בסיבוכיות זמן של ${\sqrt {q}}$ צעדים ובסיבוכיות מקום זהה. אלגוריתם רו של פולרד פותר את הבעיה בזמן דומה אך ללא צריכת זיכרון.

רקע מתמטי

אלגוריתם פוליג הלמן מנסה להאיץ את חישוב הלוגריתם הבדיד במקרה שסדר החבורה $q$ אינו ראשוני וידועים גורמים לא טריוויאליים שלו. ידוע שהסדר של האיבר $g$ הוא השלם $i$ הקטן ביותר המקיים $g^{i}=1$. יהי $q$ הסדר של $g$ ונניח שקיים שלם $p$ שהוא מחלק שלו ($p|q$) אז הסדר של $g^{p}$ הוא $q/p$. הכללה של משפט השאריות הסיני אומרת שאם ידוע הפירוק: $\textstyle q=\Pi _{i=1}^{k}q_{i}$ כאשר כל $q_{i}$ זר יחסית לגורמים האחרים (כלומר ${\text{gcd}}(q_{i},q_{j})=1$ עבור כל $i\neq j$) כאשר gcd היא מחלק משותף מקסימלי, אז קיימת התאמה או איזומורפיזם בין החבורות $\mathbb {Z} _{q_{i}}$ למכפלה הקרטזית שלהם $\mathbb {Z} _{q_{1}}\times \mathbb {Z} _{q_{2}}\times \cdots \times \mathbb {Z} _{q_{k}}$ וקיימת דרך יעילה לעבור בין הייצוגים השונים.

בהינתן היוצר $g$ ואיבר כלשהו נניח $h$ ואנחנו מעוניינים למצוא את $x$ כך שמתקיים $g^{x}=h$, נניח שהסדר של $g$ הוא $q$ וידועים לנו הגורמים שלו: $\textstyle q=\Pi _{i=1}^{k}q_{i}$ (הגורמים לא חייבים להיות ראשונים כל עוד הם זרים זה לזה), אז ידוע שמתקיים:

$(g^{q/q_{i}})^{x}=(g^{x})^{q/q_{i}}=h^{q/q_{i}}$ עבור כל $i=1,...,k$.

אם $g_{i}=g^{q/q_{i}}$ עבור כל $i$ אז מתקבלות $k$ בעיות של לוגריתם בדידי ב-$k$ חבורות, כל אחת מסדר $q_{i}$, שים לב שהסדר שלהן קטן משמעותית מ-$q$. אם נפתור את $k$ המופעים הללו בעזרת כל אלגוריתם כוח גס לפתרון בעיית לוגריתם בדיד, נוכל לפתור את הבעיה בחבורה הגדולה (נובע ממשפט השאריות הסיני). כלומר הלוגריתמים הבדידיים $x_{i}$ מ-1 עד $k$ מקיימים: $g_{i}^{x_{i}}=h^{q/q_{i}}=g_{i}^{x}$. היות ש-$x$ שקול ל-$x_{i}$ מודולו $q_{i}$ עבור כל $i$ לפי משפט השאריות הסיני למערכת המשוואות הבאה:

$x\equiv x_{1}{\text{ mod }}q_{1}$ $\vdots$ $x\equiv x_{k}{\text{ mod }}q_{k}$

יש פתרון יחיד $x$ מודולו $q$. כך שאפשר לחשב אותו מתוך $x_{1},...,x_{k}$ עם אלגוריתם כמו אלגוריתם גאוס או אלגוריתם של גרנר (מתואר בהמשך).

תיאור האלגוריתם

תיאור אלגוריתם פוליג-הלמן מתוך הספר "מבוא למתמטיקה של ההצפנה". תהי $\mathbb {G}$ חבורה ונניח שיש לנו אלגוריתם לפתרון בעיית הלוגריתם הבדיד ב-$\mathbb {G}$ עבור כל איבר מסדר שהוא חזקה ראשונית (מתואר בהמשך). למשל אם $g\in \mathbb {G}$ הוא מסדר $q^{e}$ ונניח שיש לנו אלגוריתם שפותר את הבעיה $g^{x}=h$ בסיבוכיות של $q^{e/2}$. אם הסדר של $g\in \mathbb {G}$ הוא $N$ שניתן לפירוק מהצורה $N=q_{1}^{e_{1}}\cdot q_{2}^{e_{2}}\cdots q_{k}^{e_{k}}$ אז אפשר לפתור את בעיית הלוגריתם הבדיד $g^{x}=h$ בסיבוכיות של

$O(\sum _{i=1}^{k}q_{i}^{e_{i}/2}+\log N)$ צעדים.

השיטה היא כדלהלן:

1. עבור $i=1$ עד $k$ בצע:
   1. $g_{i}=g^{N/q_{i}^{e_{i}}}$ וכן $h_{i}=h^{N/q_{i}^{e_{i}}}$
   2. שים לב, היות שכל $g_{i}$ הוא מסדר חזקה ראשונית, אפשר להשתמש באלגוריתם לפתרון בעיית הלוגריתם הבדיד עם סדר מחזקה ראשונית שמתואר להלן, כתת-שגרה שלו, כדי לפתור את הבעיה $g_{i}^{y}=h_{i}$.
   3. יהי $y=y_{i}$ הפתרון למשוואה זו.
2. משתמשים במשפט השאריות הסיני כדי לפתור את מערכת המשוואות המודולרית:

$\ \ \ \ \ \ \ \ \ \ \ \ x\equiv y_{1}{\text{ (mod }}q_{1}^{e_{1}})$, $\ \ \ \ \ \ \ \ \ \ \ \ x\equiv y_{2}{\text{ (mod }}q_{2}^{e_{2}})$, $\ \ \ \ \ \ \ \ \ \ \ \ \vdots$ $\ \ \ \ \ \ \ \ \ \ \ \ x\equiv y_{k}{\text{ (mod }}q_{k}^{e_{k}})$.

אלגוריתם פוליג-הלמן בעצם מצמצם את בעיית הלוגריתם הבדיד של איבר מסדר כלשהו לבעיית הלוגריתם הבדיד של איבר מסדר שהוא חזקה של ראשוני. לכן בעיית הלוגריתם הבדיד בחבורה $\mathbb {G}$ קלה לפתרון אם הסדר של החבורה הוא כפולה של ראשוניים קטנים. למשל במקרה של השדה $\mathbb {F} _{p}$ אם $p-1$ מתפרק לגורמים קטנים אז לא מומלץ להשתמש בשדה הזה אם רוצים חבורה שבה הבעיה נחשבת קשה. מה שאפשר לעשות זה למצוא שדה כזה כך שהראשוני $p$ שווה $2q+1$ כאשר $q$ ראשוני וכן לבחור יוצר מסדר $q$ ואז עובדים בתת-חבורה מסדר $q$ של $\mathbb {F} _{p}$ וסיבוכיות פתרון בעיית הלוגריתם הבדיד בתת-חבורה זו יהיה מסדר $O({\sqrt {q}})$. בגלל שאלגוריתם תחשיב אינדקסים הוא תת-מעריכי $q$ צריך להיות גדול.

יתרה מזו אפשר לצמצם את בעיית הלוגריתם הבדיד של איבר מסדר חזקה ראשונית לסדר ראשוני בסיבוכיות $O(e{\sqrt {q}})$ (להיפטר מהחזקה). בגלל הטריק הבא: אם $g$ הוא מסדר $q^{e}$ אז $g^{q^{e-1}}$ הוא מסדר $q$. אם חוזרים על פעולה זו מספר פעמים אפשר להגיע לפתרון הלוגריתם הבדיד. הרעיון הוא לכתוב את המעריך $x$ בצורה:

$x=x_{0}+x_{1}q+x_{2}q^{2}+\cdots x_{e-1}q^{e-1}$ כאשר $0\leq x_{i}<q$.

ואז לחשב רקורסיבית את $x_{0},x_{1},x_{2},...$. היות ש-$g^{q^{e-1}}$ הוא מסדר $q$ מזה נובע ש:

$h^{q^{e-1}}=\left(g^{x}\right)^{q^{e-1}}$ $\ \ \ \ \ \ \ \ =\left(g^{{x_{0}}+x_{1}q+x_{2}q^{2}+\cdots +x_{e-1}q^{e-1}}\right)^{q^{e-1}}$ $\ \ \ \ \ \ \ \ =g^{x_{0}q^{e-1}}\cdot \left(g^{q^{e}}\right)^{x_{1}+x_{2}q+\cdots +x_{e-1}q^{e-2}}$ $\ \ \ \ \ \ \ \ =\left(g^{q^{e-1}}\right)^{x_{0}}$

הראשון נובע מהעלאת שני האגפים של $g^{x}=h$ בחזקת $q^{e-1}$. השני נובע מההצגה המורחבת של $x$ השלישי נובע מהעובדה ש-$g^{q^{e}}=1$. לכן המשוואה:

$\left(g^{q^{e-1}}\right)^{x_{0}}=h^{q^{e-1}}$

הוא לוגריתם בדיד שהבסיס שלו הוא איבר מסדר $q$. ההנחה היא שאפשר לפתור בעיה זו ב-${\sqrt {q}}$ צעדים. אם פתרנו את המשווה הזו נוכל למצוא את $x_{0}$ עם המאפיין:

$g^{x_{0}q^{e-1}}=h^{q^{e-1}}$ בחבורה $\mathbb {G}$.

בשלב הבא מבצעים חישוב דומה והפעם מעלים את שני האגפים של $g^{x}=h$ בחזקת $q^{e-2}$ ומקבלים את:

$h^{q^{e-2}}=\left(g^{x}\right)^{q^{e-2}}$ $=\left(g^{{x_{0}}+x_{1}q+x_{2}q^{2}+\cdots +x_{e-1}q^{e-1}}\right)^{q^{e-2}}$ $=g^{x_{0}q^{e-2}}\cdot g^{x_{1}q^{e-1}}\cdot (g^{q^{e}})^{x_{2}+x_{3}q+\cdots +x_{e-1}q^{e-3}}$ $=g^{x_{0}q^{e-2}}\cdot g^{x_{1}q^{e-1}}$.

היות שאנחנו כבר יודעים את ערכו של $x_{0}$, כדי למצוא את $x_{1}$ אנחנו צריכים לחשב את הלוגריתם הבדיד

$\left(g^{q^{e-1}}\right)^{x_{1}}=\left(h\cdot g^{-x_{0}}\right)^{q^{e-2}}$.

עבור הנעלם $x_{1}$. שוב אפשר עם האלגוריתם לפתרון לוגריתם בדיד מסדר ראשוני ב-${\sqrt {q}}$ צעדים למצוא את $x_{1}$ ואז קיבלנו את $x_{0}$ ו-$x_{1}$ המקיימים:

$g^{(x_{0}+x_{1}q)q^{e-2}}=h^{q^{e-2}}$ ב-$\mathbb {G}$.

באותה דרך אפשר למצוא את $x_{2}$, באופן כללי אחרי שאנחנו יודעים מהם הערכים של $x_{0},...,x_{i-1}$ אז אפשר לחשב את $x_{i}$ על ידי פתרון:

$(g^{q^{e-1}})^{x_{i}}=(h\cdot g^{-x_{0}-x_{1}q-\cdots -x_{i-1}q^{i-1}})^{q^{e-i-1}}$ בחבורה $\mathbb {G}$. כל לוגריתם כזה ניתן לפתרון בזמן שורש $q$ צעדים. לכן אחרי $e{\sqrt {q}}$ צעדים אפשר לקבל את המעריך $x=x_{0}+x_{1}q+\cdots +x_{e-1}q^{e-1}$ המקיים $g^{x}=h$.

דוגמאות להמחשה

נתונים הערכים:

$p=11251,g=23,h=9689$.

$N=(p-1)=q_{1}^{e_{1}}q_{2}^{e_{2}}q_{3}^{e_{3}}=2\cdot 3^{2}\cdot 5^{4}$

והבעיה היא לפתור את המשוואה $g^{x}=9689$ בשדה $\mathbb {F} _{11251}^{*}$ שהוא מסדר 11250. במקרה זה פותרים את הלוגריתם הבדיד של תת-בעיות מסדר נמוך לפי הגורמים הראשוניים של $N$. שני הגורמים הראשונים קטנים לכן הפתרון שלהם טריוויאלי. להלן דוגמה לפתרון בעיית הלוגריתם הבדיד בסדר של הגורם השלישי. אנחנו מנסים לפתור את המשוואה $5448^{x}=6909$ בשדה $\mathbb {F} _{11251}^{*}$. היות שהראשוני $p=11251$ נבחר בצורה כזו ש-$p-1$ מתחלק ב-$5^{4}$ ולכן $5448$ הוא מסדר $5^{4}$ בשדה $\mathbb {F} _{11251}^{*}$. פותרים אותו בהדרגה כדי לקבל את $x$ כדלהלן:

1. הצעד הראשון הוא לפתור את המשוואה $(5448^{5^{3}})^{x_{0}}=6909^{5^{3}}$, שמצטמצמת למשוואה $11089^{x_{0}}=11089$ זה קל כי $x_{0}=1$ הוא הפתרון היחיד ובשלב זה ערכו של $x$ הוא $x=x_{0}=1$.

2. בצעד השני מנסים לפתור את:

$\left(5448^{5^{3}}\right)^{x_{1}}=\left(6909\cdot 5448^{-x_{0}}\right)^{5^{2}}=\left(6909\cdot 5448^{-1}\right)^{5^{2}}$,

שמצטמצמת למשוואה $11089^{x_{1}}=3742$. כל מה שצריך לבדוק עבור $x_{1}$ זה ערכים בטווח 1 עד 4. כך שאפשר לפתור את זה בכוח גס די בקלות. במקרה זה הפתרון הוא $x_{1}=2$, לכן בשלב זה ערכו של $x$ הוא $x=11=1+2\cdot 5$.

3. ממשיכים לצעד הבא ומנסים לפתור את:

$\left(5448^{5^{3}}\right)^{x_{2}}=\left(6909\cdot 5448^{-x_{0}-x_{1}\cdot 5}\right)^{5}=\left(6909\cdot 5448^{-11}\right)^{5}$,

שמצטמצמת למשוואה $11089^{x_{2}}=1$ לכן $x_{2}=0$ והמשמעות במקרה זה היא שערכו של $x$ נשאר 11 בשלב זה.

4. הצעד הבא והאחרון הוא לפתור את:

$\left(5448^{5^{3}}\right)^{x_{3}}=6909\cdot 5448^{-x_{0}-x_{1}\cdot 5-x_{2}\cdot 5^{2}}=6909\cdot 5448^{-11}$.

5. התוצאה האחרונה היא $11089^{x_{3}}=6320$, שהפתרון שלה הוא $x_{3}=4$ לכן התשובה הסופית היא:

$x=511=1+2\cdot 5+4\cdot 5^{3}$.

אפשר לראות שמתקיים $5448^{511}=6909$ בשדה $\mathbb {F} _{11251}^{*}$.

להלן דוגמה לאלגוריתם פוליג הלמן המשתמש במשפט השאריות הסיני כדי לחבר ביחד את כל הפתרונות לפתרון השלם. בטבלה הבאה מוצגים פתרונות שלוש תת-הבעיות:

$q$	$e$	$g^{N/q^{e}}$	$h^{N/q^{e}}$	$(g^{N/q^{e}})^{x}=h^{N/q^{e}}$
2	1	11250	11250	1
3	2	5029	10724	4
5	4	5448	6909	511

הבעיה המופיעה בשורה השלישית היא הבעיה מהדוגמה הקודמת.

בשלב זה מנצלים את משפט השאריות הסיני כדי לפתור את מערכת המשוואות המודולרית:

$x\equiv 1{\text{ (mod }}2)$ $x\equiv 4{\text{ (mod }}3^{2})$ $x\equiv 511{\text{ (mod }}5^{4})$

והפתרון הוא $23^{4261}=9689$ מודולו $11251$.

אלגוריתם גרנר לפתרון CRT

אלגוריתם גרנר לפתרון מערכת משוואות מודלרית לפי משפט השאריות הסיני.

קלט: שלם חיובי $m$ שהוא כפולה של $t$ שלמים חיוביים זרים זה לזה $m_{1}\cdot m_{2}\cdots m_{t}$ וייצוג מודולרי $v(x)=(v_{1},v_{2},...,v_{t})$ (השאריות) של $x$ מודולו כל $m_{i}$.

פלט: שלם $x$ המקיים את משוואת CRT.

1. עבור $i=2$ עד $t$ מצבעים:
   1. $C_{i}=1$
   2. עבור $j=1$ עד $(i-1)$ מבצעים:
      1. $u=m_{j}^{-1}{\text{ mod }}m_{i}$
      2. $C_{i}=u\cdot C_{i}{\text{ mod }}m_{i}$
2. $u=v_{1},x=u$
3. עבור $i=2$ עד $t$ מחשבים את: $u=(v_{i}-x)C_{i}{\text{ mod }}m_{i},x=x+u\Pi _{j=1}^{i-1}m_{j}$.
4. מחזירים את $x$.

הערות שוליים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

25215840אלגוריתם פוליג-הלמן