פונקציית גיבוב קריפטוגרפית

פונקציית גִּבּוּב קריפטוגרפית היא פונקציית גיבוב חד-כיוונית הממירה קלט באורך כלשהו לפלט קצר, באורך קבוע, הנקרא קוד גיבוב או ערך גיבוב. ערך הגיבוב משרת כייצוג קומפקטי של הקלט או כאמצעי זיהוי ייחודי שלו, מעין טביעת אצבע דיגיטלית. יש נוהגים לכנותו תמצית-מסר (message digest) ועיקר השימוש בו הוא להוכחת שלמות ואימות הקלט. אם נעשה שינוי כלשהו אפילו מינורי בתוכן הקלט לפונקציה, בסבירות גבוהה מאוד הפלט יהיה שונה לגמרי ולכן ניתן יהיה להבחין בזאת בקלות. בניגוד לפונקציית גיבוב רגילה, פונקציית גיבוב קריפטוגרפית חייבת להיות חד-כיוונית במובן שבהינתן הפלט יהיה קשה מבחינה חישובית למצוא את קלט המקור שלו ולכן יהיה קשה ביותר לגורם זדוני לזייף קלט באופן כזה שיתקבל ממנו ערך גיבוב זהה.

פונקציות גיבוב קריפטוגרפיות ממלאות תפקיד חשוב בקריפטוגרפיה מודרנית, הן מהוות חלק בלתי נפרד מפרוטוקולים קריפטוגרפיים רבים; חתימה דיגיטלית, קוד אימות מסרים, הגנה על סיסמאות, מחולל פסאודו-אקראי, אנטי-וירוס, קוד תיקון שגיאות, סכמת התחייבות ועוד.

כמו פונקציית גיבוב קונבנציונלית הנפוצה ביישומי מחשב לא קריפטוגרפיים, תפקידה העיקרי הוא למפות תחום גדול לטווח קטן, אך הן נבדלות במספר היבטים חשובים. פונקציית גיבוב כללית מקבלת קלט באורך שרירותי ומפיקה פלט באורך קבוע. בניסוח פורמלי עבור התחום $D$ והטווח $R$ תמיד מתקיים $h:D\rightarrow R,|D|>|R|$ . לפי עקרון שובך היונים העובדה שהפונקציה ממפה מקורות רבים לתמונות מעטות משמעה שבהכרח קיימות התנגשויות - שני קלטים שונים שהפונקציה מפיקה מהם פלט זהה. בהנחה שפונקציית הגיבוב רנדומלית, אם $t$ הוא אורך הקלט בסיביות ו- $n$ אורך הגיבוב בסיביות הרי שבמקרה הממוצע $2^{t-n}$ קלטים ימופו באופן זהה. במילים אחרות ההסתברות להתנגשות היא $2^{-n}$ ללא תלות ב- $t$ .

תכונות בסיסיות

השאלה האם קיימת פונקציה חד-כיוונית מוכחת מבחינה מתמטית, נובעת מהשאלה הפתוחה האם P=NP. לאור זאת לא ידוע אם ניתן ליצור פונקציית גיבוב קריפטוגרפית חד-כיוונית 'אמיתית'. עם זאת, קיימות פונקציות הנחשבות כחד-כיווניות לכל צורך מעשי שביטחונן מתואר במונחים של כח המחשוב הדרוש כדי להפוך אותן. מסיבה זו ככל שכח המחשוב עולה, נדרש להחליפן מעת לעת בפונקציות חזקות יותר. פונקציית גיבוב תקרא קריפטוגרפית אם היא מקיימת שלוש תכונות בסיסיות (לפחות את שתי הראשונות), מהקל אל הכבד:

קושי בהיפוך (preimage resistance); בהינתן פלט מסוים, מציאת הקלט המקורי שלו, קשה מבחינה חישובית. או בניסוח פורמלי, אם נתונה פונקציה הסתברותית כלשהי $h$ והמקור $x$ , מציאת $x'$ כאשר $x'\neq x$ כך שמתקיים $y=h(x')$ היא משימה קשה.
קושי במציאת מקור נוסף (2nd-preimage resistance); בהינתן קלט כלשהו יהיה קשה חישובית למצוא קלט אחר המוביל לאותו פלט, בניסוח פורמלי: בהינתן $x$ , מציאת $x'$ כאשר $x'\neq x$ כך שיתקיים $h(x)=h(x')$ .
קושי במציאת התנגשויות (collision resistance); מציאת שני קלטים שונים כלשהם המפיקים פלט זהה קשה מבחינה חישובית. בניסוח פורמלי מציאת מקורות $x,x'$ כך שמתקיים $h(x)=h(x')$ . שים לב שבניגוד להגדרה הקודמת שני הקלטים חופשיים ויכולים להיות כל ערך לפי בחירה.

מלבד זאת, פונקציית גיבוב קריפטוגרפית מקיימת את התכונות הבסיסיות של פונקציית גיבוב בכלל. קרי, כיווץ וקלות ביצוע. פונקציית גיבוב אמורה להפיק פלט שהוא קטן יותר מהקלט וכן זמן ביצועה צריך להיות יעיל במונחי מחשוב.

פונקציה חד-כיוונית העמידה בפני התנגשויות (הגדרה 3) היא החזקה ביותר והיא אינה הכרחית בכל המקרים. המודל המקובל להגדרת קושי מבחינה חישובית הוא במונחים של סיבוכיות זמן. כלומר אם נתונה הפונקציה $h:X\rightarrow Z$ , זמן הריצה האידיאלי למציאת מקור (הפיכת הפונקציה) צריך להיות מסדר גודל של $2^{|Z|}$ . לעומת זאת זמן הריצה במקרה הגרוע למציאת התנגשות מתקצר משמעותית, רק $\textstyle 2^{\frac {|Z|}{2}}$ . זאת בגלל התקפת יום הולדת שמבוססת על פרדוקס יום ההולדת.

התקפת יום הולדת

פרדוקס יום ההולדת אומר שהסיכויים שיימצאו בחדר אחד שניים מתוך 23 אנשים שלהם יום הולדת זהה, הם בערך 0.507 (מעל 50 אחוז), שזה באופן מפתיע גבוה מהאינטואיציה הראשונית (מסיבה זו נקרא 'פרדוקס'). היות שלא מדובר על יום הולדת ספציפי אלא כל זוג תואם, מספר הזוגות האפשריים בקבוצה כזו הוא רק $23\times 22/2=253$ . במילים אחרות כדי שההסתברות ששני משתנים מקריים יהיו זהים מעל מרחב הסתברות $U$ בהתפלגות אחידה בהסתברות גבוהה מחצי נדרשים לפחות $1.2\cdot |U|^{1/2}$ מאורעות. במקרה של יום הולדת השורש הריבועי של 365 הוא בערך 19.10 ולכן צריכים להיות לפחות 23 אנשים, אך בכל הקשור לימי הולדת נתון זה אינו מדויק כיוון שהתפלגות הלידות אינה אחידה (למשל באוקטובר נולדים כ-5% יותר תינוקות בממוצע מאשר בחודשים האחרים בשנה^[1]).

העובדה שמבחינה סטטיסטית היתכנות של התנגשויות גבוהה יחסית ניתנת לניצול לשבירת פונקציית גיבוב (או כל פונקציה חד-כיוונית). הרעיון הוא שהמתקיף שמקבל לידיו קלט מסוים נניח $m$ אותו הוא מעוניין לזייף ואת ערך הגיבוב שלו נניח $h(m)$ המשמש כהוכחה למקוריותו. הוא מכין תחילה $r_{1}$ וריאציות של $m$ וכן $r_{2}$ וריאציות של הקלט המזויף $m'$ אותו הוא מעוניין להחליף איתו. את כל הערכים הוא מגבב ומאחסן בטבלה ממוינת. לאחר מכן הוא מחפש בטבלה שני קלטים האחד מקורי והשני מזויף שלהם ערך גיבוב זהה. במידה שנמצא זוג תואם כזה נניח $(m_{i},m_{i}')$ הוא יכול לשייך את ערך הגיבוב של $m_{i}$ לקלט $m_{i}'$ ולטעון שהוא מקורי היות שמתקיים $h(m_{i}')=h(m_{i})$ . ההבדלים בין הקלטים יכולים להיות כל הבדל קל שאינו משנה את משמעות התוכן כמו רווחים כפולים, שורות ריקות וכדומה. מבחינה הסתברותית מספר ההתנגשויות הצפוי הוא $r_{1}\cdot r_{2}/n$ והסיכוי למצוא התנגשות אחת הוא בסדר גודל $1-\exp(-r_{1}\cdot r_{2}/2^{n})$ שהוא בערך 63% עם זיכרון בסדר גודל של $O(r)$ כאשר $r=r_{1}=r_{2}=2^{n/2}$ . יש להביא בחשבון גם את מיון הערכים שהוא בסיבוכיות של $O(r\log r)$ וכן החיפוש שהוא בסיבוכיות $O(\log r)$ אך פעולות אילו אינן משמעותיות ואפשר להתעלם מהן. את ההתקפה פיתח גידעון יובל ב-1979^[2].

יתרה מזו, אפשר לצמצם את דרישות הזיכרון באופן משמעותי אם ממירים את בעיית חיפוש ההתנגשויות לבעיה אחרת מאוד דומה שנקראת בעיית מציאת מחזוריות של פונקציה אקראית. אם נתונה פונקציה אקראית $x_{0},x_{1}=f(x_{0}),x_{2}=f(x_{1}),...$ , קיימים אלגוריתמים מהירים^[3] למציאת שני ערכים $x_{i},x_{j}$ כך שמתקיים $f(x_{i})=f(x_{j})$ כאשר $i\neq j$ וזאת ללא צורך בזיכרון כלל. בנוסף אפשר ליישם את אלגוריתם החיפוש באופן מקבילי^[4]. לדוגמה בטכנולוגיה של 1994 אפשר היה לבנות בעלות של 10 מיליון דולר, חומרה ייעודית למציאת התנגשויות בפונקציית הגיבוב MD5 כאשר $n=128$ בתוך 21 יום. בשנת 2004 במחיר נמוך מזה אפשר היה למצוא התנגשויות בתוך 4 שעות.

להתקפה זו השלכה מהותית על ביטחון כל פונקציית גיבוב. אם פונקציית גיבוב מפיקה פלט של $n$ סיביות, בהנחה שלא קיימת נגדה התקפה טובה מכוח גס אז אומרים שביטחונה המרבי הוא בפקטור של כמחצית $n$ ללא תלות באיכותה. למשל ב-SHA-1 פלט הפונקציה המינימלי הוא 160 סיביות ועל כן מציאת התנגשות בכוח גס היא בסיבוכיות של $2^{80}$ . נכון לשנת 2015 מקובל להשתמש בערכי גיבוב באורך של לפחות 256 סיביות כדי לקבל ביטחון ברמה של $2^{128}$ שהוא המינימום הנדרש כיום. ליתר דיוק מספיק שהזיכרון הפנימי של האלגוריתם יהיה גדול כדי לסכל התקפה זו ואילו ערך הגיבוב המתקבל ממנו ניתן ל"קיטום" לגודל הרצוי. הוכח שאם פונקציית הגיבוב בטוחה, הרי שאפשר ליטול רק חלק מתוצאת הגיבוב מבלי להסתכן בירידה בביטחון כל עוד אורך הגיבוב שמשתמשים בו מספיק גדול כדי למנוע ניחוש בכוח גס, למעשה זו השיטה הרווחת כיום.

שימושים

הבטחת שלמות. השימוש העיקרי בפונקציית גיבוב הוא הבטחת שלמות של פיסת מידע דיגיטלי כמו קובץ, הודעת דואר, מפתח הצפנה או מסר כלשהו. תחילה מפיקים מהמסמך תמצית קצרה אותה שולחים יחד עם המסמך או מאחסנים במקום שמור. בנקודת זמן כלשהי, אם מעוניינים לוודא את שלמות המסמך מחשבים את פונקציית הגיבוב מתוכן המסמך הנוכחי ומשווים את התוצאה מול התמצית השמורה, אם ישנו הבדל משמע שבוצע שינוי. פונקציית הגיבוב מבטיחה מעצם הגדרתה שניסיון לבצע שינוי זדוני במסמך מבלי שהמשתמשים הלגיטימיים יבחינו בו יתגלה מיד היות שתמצית המסמך השמורה לא תתאים למסמך לאחר השינוי. אלא אם כן המתקיף מסוגל לשנות גם את התמצית. היות שהתמצית בדרך כלל מאומתת בדרך כלשהי לא סביר שהוא יצליח.
חתימה דיגיטלית. פונקציית גיבוב בדרך כלל מהירה מאוד לכן מסיבות של יעילות כאשר רוצים לחתום חתימה דיגיטלית על מסמך גדול, עדיף תחילה להכין מהמסמך תמצית ולחתום עליה במקום לחתום על המסמך כולו. היות שיש התאמה חד-ערכית בין המסמך לתמצית שלו אם החתימה על התמצית נמצאת תקפה, הרי שעובדה זו מבטיחה שהמסמך עצמו אותנטי. בנוסף פונקציית גיבוב יכולה לשמש כבסיס לחתימה דיגיטלית חד-פעמית. הרעיון לחתימה דיגיטלית חד-פעמית מבוססת פונקציית גיבוב עלה כבר ב-1979 והסיבה שהיא אינה בשימוש נרחב כיום נובע בעיקר בגלל מפתחות חתימה ואימות הגדולים מדי. לאורך השנים נעשו מאמצים להקטין את המפתחות, ביניהם הרעיון של שימוש בעץ גיבוב.
הגנה על סיסמאות. שיטה ותיקה לניהול סיסמאות נעשית באמצעות פונקציית גיבוב. סיסמאות לא נשמרות במצב גלוי מחשש לפריצה למערכת וגנבתן. לא מקובל להשתמש בפונקציית הצפנה כדי להגן על סודיות הסיסמאות מפני שלוש סיבות. א. אין צורך בפענוח כלל כי אפשר להשאיר את הסיסמאות במצב מוצפן. בכל ניסיון אימות השרת יכול להצפין את הסיסמה שהוקלדה על ידי המשתמש ולהשוות את התוצאה עם הסיסמה המוצפנת השמורה במערכת. מסיבה זו פונקציית גיבוב מועדפת כי אינה זקוקה למפתח הצפנה כלל. ב. יש עניין של מגבלות חוקיות על הצפנה חזקה במדינות מסוימות כמו ישראל לכן כל דרך שנמנעת מהצפנה עדיפה. ג. פונקציית גיבוב מהירה, פשוטה ויעילה יותר מפונקציית הצפנה. לכן מקובל שהשרת מאחסן רק את קוד הגיבוב של הסיסמאות וכאשר משתמש מעוניין להתחבר הוא מתבקש להקליד סיסמה, השרת מחשב את פונקציית הגיבוב של הסיסמה שהקליד ובודק האם הערך שהתקבל תואם לזה השמור במערכת, אם כן השרת מאשר את ההתחברות. אמנם זו שיטה יעילה ומקובלת בעולם כיום אך היא אינה מספקת הגנה הרמטית. למעשה אינה מונעת לחלוטין התקפת כוח גס על קובץ הסיסמאות כולו, גם אם הסיסמאות אינן שמורות במצב קריא. המתקיף יכול לגנוב את קובץ הסיסמאות המוצפנות, לנחש סיסמאות כלשהן, לבצע גיבוב שלהן ולבדוק האם התוצאה מופיעה בקובץ, גם אם לא של משתמש ספציפי. היות שהתקפה כזו יכולה להתבצע בצורה לא מקוונת, למתקיף יש זמן בשפע.
אימות זהויות. דרך יותר בטוחה מאימות באמצעות סיסמה המציעה מה שקרוי "אימות חזק" היא סיסמה חד-פעמית. הרעיון הוצע לראשונה על ידי לזלי למפורט^[5] והוא שימוש בפונקציית גיבוב לצורך אימות זהויות ברשת לא בטוחה מבלי להשתמש בסיסמה קבועה. דוגמה למערכת כזו היא S/KEY.
סכמת התחייבות. אפשר להכין סכמת התחייבות מפונקציית גיבוב, הרעיון הבסיסי פועל כדלהלן: אם אליס רוצה להוכיח לבוב ידיעת סוד מסוים אך אינה רוצה לחשוף אותו בפניו (כעת), היא יכולה להכין תמצית גיבוב מהסוד ולשלוח אותה לבוב כהתחייבות. בבוא העת כאשר הסוד נחשף בוב יכול לייצר ערך גיבוב חדש של הסוד ולהשוותו מול זה שאליס שלחה קודם. בדרך זו בוב יכול להבטיח שאליס לא שינתה את הסוד ולמעשה הסוד שנחשף הוא הסוד שהיא התחייבה על ידיעתו קודם לכן. לסכמות התחייבות שימושים במכרז והצבעה דיגיטליים.
מחולל פסאודו-אקראי. פונקציית גיבוב קריפטוגרפית יכולה לשמש כבסיס למחולל פסאודו-אקראי. טכניקה זו מנוצלת בהרבה פרוטוקולים. במחולל פסאודו אקראי קריפטוגרפי מקובל לא להשתמש ישירות בערכים אקראיים שנאספו ממקורות שונים (כגון מחולל אקראי פיזי, פונקציה קריפטוגרפית או נתוני מערכת אקראיים חסרי חשיבות) זאת בגלל שההתפלגות הסטטיסטית שלהם עלולה להיות נמוכה, אלא תחת זאת מעבירים אותם בפונקציית גיבוב ותוצאת הגיבוב היא פלט המחולל הסופי (דוגמאות; האלגוריתמים Yarrow ו-TrueRand).
פונקציית גזירת מפתח - Key derivation function (בקיצור KDF). פונקציית גיבוב קריפטוגרפית טובה לגזירת מפתחות הצפנה רבים מתוך מפתח מאסטר יחיד. כל אימת שזקוקים למפתח חדש מבצעים גיבוב של המפתח הקודם ולוקחים חלק מהתוצאה לפי הצורך כמפתח חדש. בגלל החד-כיווניות של פונקציית הגיבוב, יהיה קשה למתקיף לנסות לנחש את המפתחות שהופקו. אך אם עלה בידו לנחש את מפתח המאסטר יהיה קל לו לנחש את כל המפתחות כי הוא פשוט יכול להריץ את פונקציית הגיבוב בעצמו.

סוגי פונקציות

פונקציות גיבוב קריפטוגרפיות מתחלקות לשתי משפחות עיקריות:

פונקציית גיבוב ללא מפתח; נקראת גם modification detection code בקיצור MDC. תפקידה להוות ייצוג תמציתי של המסר כך שיהיה אפשר לחשוף כל שינוי אפילו קל ביותר בסבירות גבוהה. דוגמאות שימוש; הגנה על סיסמאות וחתימה דיגיטלית. בסיסמאות למשל הן אינן נשמרות במצב גלוי אלא רק ערך הגיבוב שלהן נשמר ובחתימה דיגיטלית מסיבות של יעילות, החתימה מתבצעת על תמצית מהמסר במקום על המסר עצמו.

פונקציית גיבוב ללא מפתח מוגדרת באופן כללי כך:

H:\{0,1\}^{*}\rightarrow \{0,1\}^{n}

הכוכבית מציינת שאורך המידע אינו קבוע ו-

n

הוא אורך התג בסיביות (למשל 160 סיביות ב-SHA-1 או 256 סיביות ב-SHA-2).

פונקציית גיבוב עם מפתח; נקראת גם message authentication code בקיצור MAC ומשמשת בעיקר לאימות מסרים. היא מוגדרת באופן כללי כך:

H:\{0,1\}^{k}\times \{0,1\}^{*}\rightarrow \{0,1\}^{n}

k

הוא אורך המפתח בסיביות ויכול להיות בכל אורך שרירותי שמתאים לגודל הבלוק שפונקציית הגיבוב מקבלת. אפשר להפוך כל פונקציית גיבוב לפונקציית MAC עם מפתח. דרך אחת נקראת HMAC והיא שילוב בטוח של המפתח הסודי עם המסר וערכים קבועים נוספים, על ידי XOR.

מבנה מרקל-דמגרד

ערך מורחב – שיטת מרקל-דמגרד

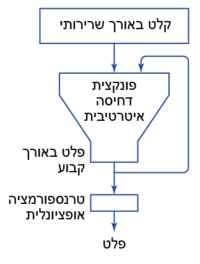
מבנה טיפוסי של פונקציית גיבוב קריפטוגרפית מורכב משלושה שלבים עיקריים; שלב הכנה, הליבה שנקראת 'פונקציית תמצות' ושלב סיום אופציונלי. היות שבדרך כלל המסר גדול במידה נכרת מהקלט אותו מקבלת פונקציית התמצות הפנימית יש צורך ליישם שיטה כלשהי לחלוקה לבלוקים בגודל קבוע וריפוד הבלוק האחרון כאשר אורך המסר אינו מתחלק היטב. השיטה הנפוצה שנקראת MD strengthening הומצאה על ידי רונלד ריבסט והיא מיישמת את מבנה מרקל ודמגרד. בשיטה זו מחלקים את הקלט לבלוקים בגודל קבוע מוסיפים '1' בסוף המסר ומרפדים באפסים ואז מוסיפים בלוק אחד המייצג את גודל המסר בסיביות ומבצעים את פעולת הפונקציה על כל הבלוקים בזה אחר זה. מרקל ודמגרד הוכיחו שאם נתונה פונקציית כיווץ (compression function) חסינת התנגשויות (בקיצור CRHF) למשל פונקציה מהצורה $F:\{0,1\}^{n}\times \{0,1\}^{k}\rightarrow \{0,1\}^{k}$ כאשר $k<n$ , אפשר להכין ממנה פונקציית גיבוב בטוחה לגיבוב מסר בכל אורך רצוי, שגם היא חסינת התנגשויות. כלומר ביטחון המבנה האמור אינו חלש מביטחונה של הפונקציה הפנימית עצמה.

פונקציית התמצות $h$ מקבלת מחרוזת סיביות $x$ באורך קבוע וערך נוסף (בדרך כלל תוצאת הפונקציה מסבב קודם הנקרא chaining value) ומחזירה פלט באורך קבוע באמצעות חישוב אלגברי כלשהו או בהסתמך על פונקציית הצפנה, לפונקציה זו תכונה חשובה שנקראת אפקט כדור השלג, הכוונה היא שכל שינוי קל בקלט אפילו בסיבית אחת יגרום לשינוי גדול בפלט, כך בתוך מספר סבבים מיטשטש הקשר בין הקלט המקורי לפלט.

כמתואר בתרשים השיטה באופן כללי פועלת כדלהלן:

הקלט $x$ מחולק ל- $t$ בלוקים בגודל $r$ סיביות, $x=x_{1},x_{2},...,x_{t}$ .
אם $|x|$ (אורך $x$ בסיביות) אינו מתחלק ב- $r$ בשלמותו מוסיפים '1' בבלוק $x_{t}$ לאחר המידע ומשלימים באפסים. תוספת זו מכונה MD strengthening והיא הוכנסה לראשונה באלגוריתם MD4 של רונלד ריבסט.
מוסיפים בלוק $x_{t+1}$ שמכיל ייצוג של אורך המסר בסיביות.
מכינים וקטור אתחול בגודל $r$ סיביות, נקרא בקיצור $IV$ ומציבים בבלוק $H_{0}$ .
מבצעים איטרציה של הפונקציה הפנימית; עבור כל הבלוקים $x_{i}$ כאשר $i=1,...,t+1$ מבצעים $H_{i}=h(H_{i-1},x_{i})$ . בכל סבב $h$ מפיקה ערך ביניים $H_{i}$ שנקרא chaining value שהוא תוצאת החישוב על הבלוק הנוכחי בשילוב עם פלט הבלוק הקודם $H_{i-1}$ . מבנה הפונקציה הפנימית ואופן שילוב הערכים משתנה בהתאם לשיטה עליה בנוי האלגוריתם (כמתואר תרשים). בגמר כל הסבבים הפלט הוא $H_{t}$ .
לסיום טרנספומציה אופציונלית $g$ ממירה את הפלט האחרון לתוצאה הסופית $h(x)$ .

לסיכום האלגוריתם נראה כך:

H_{0}=IV,\ H_{i}=h(H_{i-1},x_{i}),\ 1\leq i\leq t;\ h(x)=g(H_{t})

פונקציית תמצות

פונקציית התמצות שנקראת גם פונקציית כיווץ (compression function) היא הליבה של פונקציית הגיבוב. אפשר להכין פונקציית תמצות חד-כיוונית וחסינת התנגשויות בשלושה אופנים עיקריים;

פונקציית תמצות מבוססת צופן בלוקים; קיימים שלושה מודלים בטוחים לבניית פונקציית תמצות על בסיס צופן בלוקים (כמתואר בתרשים).

לפי מודל מטיאס-מאייר-אוסאס (האיור השמאלי בתרשים) הפונקציה היא $H_{i}=E_{g(H_{i-1})}(x_{i})\oplus x_{i}$ .
לפי מודל דויס-מאייר הפונקציה היא $H_{i}=E_{x_{i}}(H_{i-1})\oplus H_{i-1}$ .
לפי מודל מיאגוצ'י-פרניל הפונקציה היא $E_{g(H_{i-1})}(x_{i})\oplus x_{i}\oplus H_{i-1}$ .

באופן כללי הסתמכות על צופן בלוקים לבניית פונקציית גיבוב איטית יחסית ואינה נפוצה בשימוש.

פונקציית תמצות ייעודית; זוהי פונקציה חד כיוונית חסינת התנגשויות (CRHF) שמבצעת סדרה של פעולות אריתמטיות בסיסיות תוך מתן דגש על ביצוע יעיל וקל ליישום במחשב הן בתוכנה והן בחומרה. קיימים מספר אלגוריתמים פופולריים שמסתמכים על פונקציית תמצות ייעודית. ביניהם אפשר למנות את משפחת תמצית המסרים של רונלד ריבסט, MD4 ו-MD5 וכן משפחת SHA בה כלולים שלושה אלגוריתמים SHA-2, SHA-1 ו-SHA-3 וכן RIPE-MD. שני האחרונים במשפחת SHA מומלצים כתקן גיבוב רשמי של ממשלת ארצות הברית המנוהל על ידי NIST.
פונקציית גיבוב מבוססת אריתמטיקה מודולרית. פונקציה חד כיוונית שמסתמכת על בעיה מתורת המספרים שמאמינים שהיא קשה. סכמות מסוג זה בדרך כלל איטיות מאוד ומגיעות לתפוקה של בערך ${\text{log}}_{2}{\text{log}}_{2}N$ סיביות פר העלאה בחזקה מודולרית אחת. $N$ נקרא המודולוס והוא בדרך כלל בסגנון RSA - כפולה של שני מספרים ראשוניים סודיים $N=pq$ . יש לציין שבמקרה של פונקציית גיבוב בעלת מבנה אלגברי כמו זו מכילה חולשה מובנית, קל להחדיר דלת אחורית לפרמטרים של הסכמה כדי לגרום להתנגשויות. מלבד זאת חלק מהפרמטרים אמורים להיות נסתרים מהעין, למשל הגורמים הראשוניים של $N$ , ואסור לאף צד לראותם. לכן יש צורך לנקוט משנה זהירות בבחירת הפרמטרים. דרך אחת היא להיעזר בצד שלישי מהימן, ודרך אחרת היא שימוש בסכמת שיתוף בטוחה.

פונקציית גיבוב מבוססת אריתמטיקה מודולרית

איוון דמגרד הציע סכמה כזו המבוססת על צופן אל-גמאל וגיבסון ובלייר הציעו מבנים דומים המבוססים על בעיית לוגריתם דיסקרטי שפועלים מעל חבורה $G$ מסדר ראשוני $p$ . הרעיון הוא להכפיל את $t$ הבלוקים של המסר עם $t$ אלמנטים אקראיים $\alpha _{i}$ מתוך $G$ . ערך הגיבוב יהיה תוצאה של:

H_{t+1}=\prod _{i=1}^{t}\alpha _{i}^{{\hat {X}}_{i}}

(מודולו

p

).

כאשר ${\hat {X}}_{i}$ הוא הבלוק $X_{i}$ של המסר לאחר שרופד ב-'1' כדי למנוע מצב שהבלוק יהיה כולו מאופס. בכל אופן מרבית הסכמות המבוססות על אריתמטיקה מודולרית כמו זו הן סכמות שפותחו בשיטות אד הוק, לא הוכחו כבטוחות וחלקן הגדול אף נפרצו בקלות. במיוחד ראוי לציון תקן איזו 4–10118 (MASH) שנפרץ פעם אחר פעם באופן מביך, לאחר שתוקן ובכל פעם התגלו בו שוב חולשות. המבנה הכללי הטוב ביותר היודע הוא מהצורה:

{\boldsymbol {H_{i}=((X_{i}\oplus H_{i-1})^{2}\ {\text{mod }}N)\oplus H_{i-1}}}

.

כאשר $H_{i-1}$ הוא ערך הביניים ו- $X_{i}$ הם הבלוקים של המסר עם יתירות מוספת. חשוב מאוד להוסיף יתירות מכוונת למסר לפני הגיבוב כדי למנוע את 'התקפת בלוק מתקן' (להלן). הגרסה העדכנית של תקן איזו 4–10118 נכון לשנת 1998 (ISO/IEC 10118-4) נקראת MASH קיצור של modular arithmetic secure hash והיא מופיעה בשתי גרסאות MASH-1 ו-MASH-2. פונקציית התמצות הפנימית של MASH היא מהצורה:

H_{i}=((({\hat {X}}_{i}\oplus H_{i-1})\lor A)^{2}\ ({\text{mod }}N))\dashv n\oplus H_{i-1}

כאן $A={\text{0xF00..00}}$ הוא קבוע (בבסיס הקסדצימלי) וכן את הבלוקים ${\hat {X}}_{i}$ בגודל $n$ סיביות מכינים על ידי שמחלקים תחילה את המסר לבלוקים בגודל $n/2$ סיביות ומרחיבים כל בלוק על ידי הוספת יתירות, מחלקים את המידע לחצאי בתים ומציבים '1111' בארבע הסיביות המשמעותיות הנותרות של כל בית. הסימן $\lor$ מייצג OR, הסימן $\oplus$ מייצג XOR והסימן $\dashv$ אומר שתוצאת ההעלאה בריבוע נחתכת בכל סבב ל- $n$ סיביות האחרונות. בנוסף התקן מגדיר פונקציה מסיימת מסובכת שנועדה למחוק כל זכר של המבנה האלגברי של הפונקציה. התוצאה האחרונה של פונקציית התמצות $H_{t+1}$ מחולקת ל-4 תת-בלוקים, איתם מחשבים ברקורסיה עוד שנים-עשר בלוקים בגודל $n/4$ סיביות $Y_{i}=Y_{i-1}\oplus Y_{i-4}$ , מאחדים את כל 16 הבלוקים שנוצרו לשמונה בלוקים בני $n/2$ סיביות $X_{t+1+i}=Y_{2i-2}\ \|\ Y_{2i-1}$ , מרחיבים אותם לפי השיטה האמורה לעיל ומבצעים עוד שמונה סבבים של פונקציית התמצות על הבלוקים האחרונים. ולסיום התוצאה הסופית היא מחרוזת סיביות בגודל $n/2$ המחושבת על ידי $H_{t+1+8}{\text{ mod }}p$ . ההתקפה הטובה ביותר הידועה כנגד מבנה זה היא בסיבוכיות של $2^{n/2}$ שהיא לא יותר טובה מכוח גס. MASH-2 היא גרסה שונה במעט שבה ההעלאה בריבוע מוחלפת ב- $e=2^{8}+1$ .

התקפת בלוק מתקן

התקפת בלוק מתקן (correcting block) היא התקפה המנצלת את המבנה האלגברי של פונקציית התמצות הפנימית. ההתקפה מתמקדת בחיפוש התנגשויות או מקור נוסף על ידי החלפת בלוק אחד או יותר בסוף, באמצע או בהתחלה של המסר. ההתקפה מתבצעת על ידי חישוב $h(X\ \|\ Y)$ כאשר $Y$ הוא הבלוק המתקן. מבנה אלגברי פגיע במיוחד להתקפה זו משום שאפשר להפוך לפעמים את פונקציית התמצות הפנימית בעזרת מניפולציה אלגברית. דרך נפוצה להתמודד עם התקפה זו היא להוסיף יתירות מכוונת למסר לפני הגיבוב כך שיהיה קשה למצוא בלוק מתקן עם היתירות הדרושה. המחיר כמובן הוא ירידה בביצועים. לדוגמה ב-1984 הציעו דייוויס ופרייס פונקציית גיבוב עם פונקציית תמצות $f$ כדלהלן: $f=(H_{i-1}\oplus X_{i})^{2}{\text{ mod }}N$ . היתירות שהם הוסיפו הייתה 64 אפסים שנוספו לכל בלוק לפנים או בסוף. גיראולט ואחרים הראו כיצד אפשר לתקוף פונקציה כזו ולמצוא מקור נוסף. CCITT X.509 הייתה פונקציית גיבוב שפותחה ב-1988 וניסתה למנוע את ההתקפה המתוארת על ידי הוספת היתירות באופן כזה שכל ניבל (חצי בית) בכל הבתים של המסר יכיל ארבעה אפסים. למרות זאת הראה קופרשמידט שאפשר למצוא התנגשויות במבנה זה באמצעות ההתקפה האמורה.

מבנה ספוג

ערך מורחב – פונקציית ספוג

פונקציית ספוג היא כלי קריפטוגרפי ורסטילי שיכול בין היתר לשמש כבסיס להכנת פונקציית גיבוב על ידי מה שקרוי "מבנה ספוג". מבנה ספוג הוא מצב הפעלה של פרמוטציה קבועה, עם כלל ריפוד מתאים, שמקבל כקלט מחרוזת בינארית $\mathbb {Z} _{2}^{*}$ בכל אורך, מכיל זיכרון פנימי רחב ומפיק פלט $\mathbb {Z} _{2}^{n}$ כאשר $n$ מוגדר על ידי המשתמש. מבנה ספוג הוא הכללה של פונקציית גיבוב באופן שמאפשר קלט קבוע כמו בצופן זרם או פלט קבוע כמו באימות מסרים. הוא מכיל זיכרון, דהיינו הפונקציה הפנימית מופעלת באופן איטרטיבי על המצב הפנימי בשילוב עם הקלט. את ביטחון האלגוריתם מבטאים במונחים של גודל הזיכרון הפנימי. בפונקציית ספוג נעשה שימוש בפועל בכמה אלגוריתמים חדשים, ביניהם SHA-3.

פונקציית גיבוב אקראית

פונקציית גיבוב אקראית היא פונקציית גיבוב המשלבת בנוסף לקלט הרגיל גיוון אקראי הנקרא מלח (salt). מהיבט תאורטי המטרה של המלח היא לאפשר הסתמכות על פונקציית גיבוב בעלת ביטחון חלש כמו MD5 ו-SHA-1 שבעקבות קרפיטואנליזה חדשה שמצביעה על בעיות בעמידות מפני התנגשויות מומחים המליצו שלא להשתמש בהן. הרעיון הוצע ב-2007 על ידי שי הלוי והוגו קרווציק לחיזוק אלגוריתם חתימה דיגיטלית DSA, המשלב בין היתר פונקציית גיבוב^[6]. השאיפה היא שאלגוריתם החתימה יישאר בטוח אפילו אם פונקציית הגיבוב איתה הוא משתמש אינה מספקת עמידות מפני התנגשויות בעקבות קריפטואנליזה חדשה שמצביעה על חולשות במבנה הפנימי שלה, בדיוק כמו שקרה עם MD5 ו-SHA-1. במילים אחרות מנגנון חתימה דיגיטלית שעושה שימוש בפונקציית גיבוב אקראית לא חייב להסתמך על ההנחה שקשה למצוא התנגשויות בפונקציית הגיבוב שהיא הגדרה מחמירה ובדרך כלל קשה יותר להשגה אלא על הגדרה קלה יותר הנקראת "פונקציית גיבוב אוניברסלית".

פונקציית גיבוב אוניברסלית

פונקציית גיבוב אוניברסלית או בשמה האחר TCR קיצור של Target Collision Resistance היא פונקציית גיבוב אקראית שאינה עמידה מפני התנגשויות באופן מלא. פונקציה זו פותחה בהשראת נאור ויונג^[7] שהציעו לראשונה את פונקציית הגיבוב האוניברסלית בקיצור UOWHF ששמה שונה לאחר מכן על ידי בלייר ורוגווי^[8] ל-TCR.

בניסוח רשמי, פונקציית גיבוב אוניברסלית היא בעצם משפחה של פונקציות $\{H_{r}\}_{r\in R}$ עבור קבוצה כלשהי $R$ . היא תקרא אוניברסלית או TCR אם לא קיים אלגוריתם יעיל $A$ שאיתו אפשר לנצח במשחק הבא למעט בהסתברות זניחה. $A$ בוחר קלט כלשהו $M$ ומקבל ערך אקראי $r\in _{R}R$ והוא צריך למצוא קלט אחר $M'\neq M$ כך שמתקיים $H_{r}(M')=H_{r}(M)$ . כאשר $H$ היא פונקציית גיבוב כמו MD5 והערך $r$ הוא מעין מפתח ונקרא גם "מלח". למתקיף אין שליטה על ערך זה, הוא חייב לקבל אותו עבור כל מסר שהוא מנסה לגבב. בדרך זו אפשר להפוך כל פונקציית גיבוב דטרמיניסטית ל-TCR. המלח $r$ יכול להיות ערך קצר כלשהו אך חייב להיות חד-פעמי עבור כל מסר נתון.

מבנה זה נחשב יעיל ומבטיח קושי רב יותר במציאת התנגשויות כלומר למצוא $y$ המקיים $H_{r}(x)=H_{r}(y)$ מאשר במודל הסטנדרטי של פונקציות גיבוב. כאן התקפת יום הולדת אינה ישימה כיוון שהיא לא יכולה להיות אוף ליין, כלומר התוקף חייב לקבל בנוסף לתמצית הקלט את $r$ שמיוצר באופן אקראי עבור כל מסר, לכן אפשר להסתפק בכל פונקציית גיבוב במבנה מרקל דמגרד שהיא בעלת עמידות מפני מציאת מקור נוסף ואינה חסינת התנגשויות (הגדרה 3 לעיל). הגדרה פורמלית של פונקציית גיבוב TCR היא:

H_{r}^{c}(M)=H_{r}^{c}(m_{1},m_{2},...,m_{L})\ {\overset {\underset {\mathrm {def} }{}}{=}}\ H^{c}(m_{1}\oplus r,m_{2}\oplus r,...,m_{L}\oplus r)

פשוט הקלט לפונקציית הגיבוב מחובר עם מחרוזת המלח הקצרה בלוק אחר בלוק ב-XOR לפני שמפעילים את פונקציית הגיבוב. בגלל השימוש במלח האקראי $r$ לא תמיד הפונקציה ניתנת לשימוש כחלק ממנגנון חתימה דיגיטלית כי יש צורך לחתום גם על המלח ושלוח אותו יחד עם המסר לצד המקבל, מה שמחייב שינויים משמעותיים בקוד המקור של המערכות הקיימות. אפשר לפתור את הבעיה על ידי הכללת $r$ כחלק מהמסר כך:

{\tilde {H}}_{r}^{c}(M)=H_{r}^{c}(0|M)\ {\overset {\underset {\mathrm {def} }{}}{=}}\ H^{c}(r,m_{1}\oplus r,m_{2}\oplus r...,m_{L}\oplus r)

.

כאן בנוסף לחיבור מחרוזת המלח הקצרה עם כל הבלוקים של הקלט, משרשרים את מחרוזת המלח עצמה בראש הקלט ואת הכול ביחד מגבבים עם פונקציית הגיבוב כרגיל. גרסה זו נקראת eTCR והיא מציעה ביטחון רב יותר, יתרונה הוא שאין צורך לחתום על המלח בנפרד וניתן להכניס את השינוי במערכות הקיימות ללא שינויים מרחיקי לכת בקוד המערכת.

תקן פונקציית גיבוב בטוחה (SHA)

ערך מורחב – Secure Hash Algorithm

במטרה ליצור תקן בין-לאומי אחיד של פונקציות גיבוב קריפטוגרפיות פרסם המכון הלאומי לתקנים וטכנולוגיה האמריקאי את תקן SHA קיצור של secure hash algorithm. בשנת 1993 פורסמה הראשונה מבין הפונקציות במשפחה שנקראה SHA-0 (האפס נוסף מאוחר יותר כדי להבדילה מהגרסאות המתקדמות). הפונקציה הוחלפה ב-1995 בגרסה המחוזקת SHA-1, עקב חולשות שנתגלו בה. SHA-1 דמתה ל-SHA-0 בשינויים קלים. שתי הפונקציות מבוססות על אלגוריתם תמצית מסרים של רונלד ריבסט MD5, פועלות בשיטת מרקל-דמגרד ומפיקות פלט באורך 160 סיביות. ב-2002 פרסם NIST את משפחת הפונקציות SHA-2, המפיקות ארבעה פלטים אפשריים 224, 256, 384 ו-512 סיביות.

משפחת SHA היא סדרת פונקציות גיבוב ייעודיות המבוססות על הידע שנצבר בעקבות סדרת האלגוריתמים MD (תמצית מסרים). פונקציות אלו נבנו תוך שימת דגש על פיזור אחיד של כל סיביות המסר באופן כזה שלכל חלקי המסר תהיה השפעה על הפלט. הפונקציות משתמשות בפעולות פשוטות כמו XOR, Shift ו-Rotate הבנויות כסדרה של פונקציות לוגיות המקבלות שלושה ערכים ומפיקות ערך אחד בגודל קבוע. כאשר ב-SHA1 וכן SHA256 הערכים בגודל מילה (32 סיביות) ואילו ב-SHA384 ו-SHA512 הערכים בגודל מילה כפולה (64 סיביות). ההבדל העיקרי בין הפונקציות השונות במשפחה הוא בכמות סיביות הפלט וערכי האתחול הקבועים.

בנובמבר 2007 הושקה תחרות פתוחה לתקן SHA החדש, בדומה לתחרות שהתקיימה לצפני בלוקים שבה זכה AES. באוקטובר 2012 נסגרה התחרות והוכרז Keccak האלגוריתם הזוכה בתחרות, זה שיחליף בהדרגה את קודמו לתפקיד ונקרא SHA-3. בארגון התקינה ממליצים שלא להשתמש יותר ב-SHA-1 וממליצים לעבור ל-SHA-2 או SHA-3. בארגון התקינה רואים בתקן SHA-2 עדיין בטוח לשימוש נכון לשנת 2013 ולא מתוכנן להחליפו בזמן הקרוב. העובדה ש-SHA-3 שונה מאוד בעיצובו ואופן פעולתו מתקן SHA-2 רק מרחיב את האפשרויות כיוון שלא סביר שתמצא התקפה אחת שתהיה יעילה כנגד שניהם. Keccak הזוכה בתחרות SHA-3 הוא אלגוריתם גיבוב יעיל ובטוח, שפותח על ידי קריפטוגרפים בלגיים ואיטלקיים. הוא מצטיין בגמישות רבה, שולי ביטחון גבוהים, ביצועים כלליים טובים ומימוש יעיל בחומרה. באלגוריתם זה הוכנס לראשונה מבנה הספוג הנחשב למבנה יעיל ובטוח.

פונקציות גיבוב

להלן רשימה חלקית של פונקציות גיבוב פופולריות, חלקן חדשות, חלקן היו בשימוש נרחב בעשור האחרון וחלקן לא בטוחות לאחר שהתגלו בהן חולשות והן מובאות כאן רק למען התיעוד. SHA-0 לא נכלל ברשימה גם משום שאינו בטוח כלל וגם משום שהוחלף בגרסאות מחוזקות שלו SHA-1 ו-SHA-2. ב-2005 דווחה התקפה תאורטית כנגד SHA-1 שמוצאת התנגשויות בזמן של $2^{69}$ פעולות גיבוב (לעומת $2^{80}$ כפי שמצפים מפונקציית גיבוב של 160 סיביות) ואף על פי שב-2010 דווחה התקפה מעשית בסדר גודל של $2^{61}$ , הוא נכלל ברשימה כי עדיין נפוץ בשימוש נרחב. MD5 נפרץ לגמרי. ב-2004 בתוך ארבעה חודשים נמצאו התנגשויות בגרסה מלאה של MD5 בפרויקט שנקרא MD5CRK. ב-2005 ארג'ן לנסטרה הראה שאפשר לזייף סרטיפיקט X.509 בגרסה שעושה שימוש ב-MD5 באמצעות חיפוש התנגשויות בפונקציית הגיבוב, בתוך מספר שעות. ב-2010 דווחה התקפה נוספת, היעילה ביותר עד כה כנגד MD5 שפרטיה לא פורסמו אלא הוצעה כאתגר בסך 10,000 דולר למי שיצליח למצוא התנגשות עם 64 בתים עד ינואר 2013. ייתכן שהאלגוריתם נמצא עדיין בשימוש מוגבל והוא למעשה מוחלף כעת בהדרגה על ידי ארגוני התקינה הבינלאומיים באלגוריתם בטוח יותר.

להלן הרשימה:

שם הפונקציה	אורך התג בסיביות
GOST	256
HAVAL	128/160/192/224/256
MD5	160
RIPEMD	128/160/256
SHA-1	160
SHA-2	224/256/512
SHA-3	224/256/384/512
Tiger 2	192/128/160
Whirlpool	512
Skein	256/512/1024
BLAKE	224/256/384/512

שלושת האלגוריתמים הראשונים HAVAL, GOST, MD5 וכן RIPEMD-128 לא מומלצים לשימוש כיום, והם מופיעים לצורך התיעוד בלבד. כמו כן ארגוני התקינה המליצו לעבור ל-SHA-2 ולא להשתמש יותר ב-SHA-1.

ראו גם

SHA

לקריאה נוספת

Douglas R. Stinson, Cryptography, Theory and Practice, CRC press, 1995. מסת"ב 0-8493-8521-0

קישורים חיצוניים

מדיה וקבצים בנושא פונקציית גיבוב קריפטוגרפית בוויקישיתוף

הערות שוליים

^ דו"ח: באיזה חודש נולדים הכי הרבה תינוקות?
^ Yuval, G. (1979). “How to swindle Rabin.” Cryptologia, 3,187-189.
^ Jean-Jacques Quisquater Jean-Paul Delescaille Philips Research Laboratory Belgium (1990).“How easy is collision search? Application to DES.” Advances in Cryptology-EUROCRYPT’89, Lecture Notes in Computer Science, vol. 434
^ Paul C. van Oorschot and Michael J. Wiener, (1999). “Parallel collision search with cryptanalytic applications.” Journal of Cryptology, 12(1), 1-28.
^ Password Authentication with Insecure Communication
^ Strengthening Digital Signatures via Randomized Hashing, Shai Halevi and Hugo Krawczyk, January 30, 2007
^ Moni Naor and Moti Yung, “Universal One-Way Hash Functions and their Cryptographic Applications”, STOC 1989
^ Mihir Bellare and Phillip Rogaway, “Collision-Resistant Hashing: Towards Making UOWHFs Practical”, CRYPTO 97, LNCS 1294, 1997

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

פונקציית גיבוב קריפטוגרפית31496938Q477202

[1] דו"ח: באיזה חודש נולדים הכי הרבה תינוקות?

[2] Yuval, G. (1979). “How to swindle Rabin.” Cryptologia, 3,187-189.

[3] Jean-Jacques Quisquater Jean-Paul Delescaille Philips Research Laboratory Belgium (1990).“How easy is collision search? Application to DES.” Advances in Cryptology-EUROCRYPT’89, Lecture Notes in Computer Science, vol. 434

[4] Paul C. van Oorschot and Michael J. Wiener, (1999). “Parallel collision search with cryptanalytic applications.” Journal of Cryptology, 12(1), 1-28.

[5] Password Authentication with Insecure Communication

[6] Strengthening Digital Signatures via Randomized Hashing, Shai Halevi and Hugo Krawczyk, January 30, 2007

[7] Moni Naor and Moti Yung, “Universal One-Way Hash Functions and their Cryptographic Applications”, STOC 1989

[8] Mihir Bellare and Phillip Rogaway, “Collision-Resistant Hashing: Towards Making UOWHFs Practical”, CRYPTO 97, LNCS 1294, 1997

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]