RC4

צופן RC4 הוא צופן זרם א-סינכרוני המיועד לתוכנה, פשוט ביותר וקל ליישום והטמעה בחומרה ובתוכנה. עקב פשטותו הרבה היה בעבר בשימוש נרחב בפרוטוקולי אבטחה רבים כגון SSL לאבטחת תעבורת הרשת וכן WEP. אולם עקב חולשות שהתגלו בו הוא אינו בטוח ואינו מומלץ לשימוש קריפטוגרפי כיום, אף על פי שעדיין נתמך בכמה פרוטוקולי אבטחה עקב תאימות לאחור.

RC4 פותח על ידי רונלד ריבסט ב-1987 במעבדות RSA. שמו נגזר מראשי התיבות Rivest Cipher 4, אולם לעיתים מפרשים RC כ-Ron's code (הקוד של רון). פיתוחים נוספים שלו הם RC5 וכן RC6 שנימנה בין המועמדים המובלים לתקן ההצפנה החדש שבו זכה AES. עד 1994 נשמר צופן RC4 כסוד מסחרי עד שפורסם ברבים, תחילה באופן אנונימי בקבוצות דיון קריפטוגרפיות ומשם עשה דרכו לרשת האינטרנט. ריבסט לא רשם כל פטנט על הצופן שלו, השם RC4 הוא סימן מסחרי ומוגן בזכויות יוצרים, אולם באופן לא רשמי השימוש בצופן מותר, אם כי לא תחת שמו המקורי. היות שמעבדות RSA מעולם לא פרסמו את פרטי האלגוריתם באופן רשמי, יש המכנים אותו ARCFOUR שפירושו "כביכול RC4".

הליך ההצפנה

צופן RC4 מייצר רצף סיביות פסבדו-אקראי הנקרא "זרם מפתח" באמצעות מחולל פסבדו-אקראי (PRG) מובנה. זרם הסיביות האקראי משולב עם הטקסט הקריא בית אחר בית, באמצעות חיבור בינארי (XOR) בדומה לצופן ורנם. פענוח מתבצע בדרך זהה. הזיכרון הפנימי או המצב הפנימי (internal state) של האלגוריתם מורכב משני חלקים:

תיבת תמורה $\ S$ .
שני אינדקסים $\ i$ ו- $\ j$ .

זרם המפתח שבעזרתו מצפינים את המסר מופק באמצעות אלגוריתם הכנת מפתח - Key Scheduling Algorithm (בקיצור KSA). תחילה המערך $S$ מאותחל ולאחר מכן באמצעות פונקציית החלפה Swap מערך הבתים מעורבב תוך שימוש בכל בתי מפתח ההצפנה בטכניקה הקרויה Shuffle בדומה לערבוב קלפים והתוצאה היא תמורה פסאודו-אקראית שאיתה הצופן מייצר בשלב הבא את זרם המפתח (key stream). המפתח הסודי יכול להיות בכל אורך רצוי בין 40 ל-256 סיביות. להלן תיאור שתי הפונקציות של הצופן - תהליך ההכנה KSA והמחולל הפנימי PRGA (קיצור של Pseudo-Random Generaion Algorithm), כאשר הקלט הוא מערך $K$ באורך $kLength$ בתים המכיל את המפתח הסודי שמסופק על ידי המשתמש. $N$ מייצג את מספר האלמנטים במערך $S$ וכן את הערך המקסימלי של כל אלמנט, בדרך כלל $N=256$ זה אומר 256 כניסות של אלמנטים בגודל בית אחד ( $2^{8}$ ).

$\mathbf {RC4\ KSA:}$ ${\text{For }}i=0{\text{ to }}N-1{\text{ do: }}$ $S[i]=i$ הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle j = 0} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{For }i = 0\text{ to }N - 1\text{ do:}} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle j = j + S[i] + K[i\text{ mod }kLength]} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Swap}(S[i], S[j])}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{RC4 \ PRGA:}} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle i = j = 0} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{Loop:}} $i=i+1$ הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle j = j + S[i]} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Swap}(S[i], S[j])} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Return: }S[S[i] + S[j]]}	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Swap}(S[x],S[y])} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle t = S[x]} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle S[x]=S[y]} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle S[y]=t} ‎ ‎ ‎

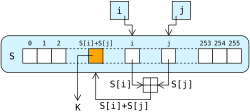
ההצפנה מתבצעת על ידי PRGA בית אחר בית במספר החזרות הנדרש עד להצפנת כל הטקסט הקריא. בכל סבב של PRGA האלגוריתם מעדכן את מצב הצופן ומפיק בית אחד של זרם המפתח. האינדקס $i$ מקודם צעד אחד, הערך המצוי בכניסה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} במערך הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle S} מוסף ל-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle j} , ערכי הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_i} ו-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_j} מחליפים מקומות (Swap) והפלט הוא הכניסה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle S[S_i + S_j]} אותה מחברים עם בית הטקסט הקריא הנוכחי. כל פעולות החיבור בצופן מבוצעות מודולו 256 (גודל בית אחד). כל כניסה במערך הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle S} מוחלפת לפחות פעם אחת כל 256 סבבים.

לדוגמה אם מפתח ההצפנה הוא "Secret" ומחרוזת הטקסט היא "Attack at dawn" התוצאה תהיה:

RC4("Secret", "Attack at dawn") = 45A01F645FC35B383552544B9BF5

יישומים

צופן RC4 אידיאלי ליישום בתוכנה, במיוחד לאור העובדה שהצופן מטפל במידע בבתים ולא סיביות. הזיכרון הנדרש לצופן הזה נמוך ביותר (רק 256 בתים). ופעולת מודולו 256 אפשר לבצע באמצעות אופרטור בינארי AND ולהימנע מחילוק (פעולה בזבזנית יותר) ובמיוחד שבפלטפורמות רבות התקן הוא שפעולת חיבור או כפל בבתים מניבה תוצאה בגבולות בית אחד כאשר התוצאה למעשה נחתכת. כלומר כיוון שהמהדר מבצע מודולו באופן עקיף, אפשר פשוט לבצע פעולות כפל וחיבור רגיל ולהתעלם לחלוטין מהמודולו.

בטחון

לצופן RC4 חסרונות ידועים רבים. זרם המפתח המיוצר באמצעות המחולל הפנימי של האלגוריתם סובל מהטיה קלה ועל כן אינו אקראי לגמרי. ישנה התקפה המנצלת עובדה זו כדי לפצח את הצופן. לכן רצוי לדלג לפחות על 512 הבתים הראשונים שנוצרו על ידי המחולל.

כדי למנוע התקפת גלוי-ידוע (chosen plaintext attack), צפנים מודרניים מצרפים וקטור אתחול לצד המפתח כדי להבטיח שהצפנה חוזרת של טקסט קריא זהה, תניב טקסט מוצפן שונה. RC4 אינו מיישם טכניקה זו על כן הזרם המוצפן חלש. כלומר בהינתן טקסט קריא זהה הפלט יהיה תמיד זהה (אם משתמשים באותו מפתח). עובדה זו מהווה נקודת תורפה שניתן לנצלה כדי לתקוף את הצופן. שרשור מספר אקראי למפתח הסודי כפי שנעשה בפרוטוקול WEP בעבר, אינו בטוח ואף הוביל להתקפה מוצלחת. דרך טובה יותר היא למזג את המפתח עם ערך אקראי באמצעות פונקציית גיבוב עם מפתח.

להלן תקציר החולשות והפגמים שהתגלו במרוצת השנים מאז פרסומו של RC4 ב-1994.

KSA תהליך הכנת זרם המפתח

בתהליך ההכנה הראשוני של RC4 המפתח הסודי המסופק על ידי המשתמש מעורבב בתוך תמורה $S$ באורך 256 בתים שנקראת המצב הפנימי (interenal state) של הצופן. קיימת הטיה סטטיסטית^[1] של בתים מהתמורה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle S} למפתח הסודי, כלומר קיים מתאם גבוה בין הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle S[v]} עבור הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle v} קטן לבין בתים של המפתח^[2]^[3]^[4]^[5].
קיימת הטיה סטטיסטית^[6]^[7] של התמורה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle S} הראשונה (המצב הפנימי) מיד לאחר KSA לצירוף כלשהו של בתים מהמפתח הסודי. קיימת נוסחה מפורשת של ההסתברויות שבתים מהתמורה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle S} בכל שלב נוטים לבתים של המפתח הסודי.
מבחינה תאורטית, קיימת חולשה מובנית^[8]^[9] בסגנון העירבוב של KSA שגורם לכך שהתמורה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle S} אינה אחידה לגמרי, אלא סובלת מחוסר אקראיות בכמה מקומות, מה שיכול להוביל להתקפת הבחנה^[10].
בתהליך הכנת זרם המפתח קיימת תופעה מעניינת שנקראת "זוגות אנומליה", מספר הפעמים הצפוי שבהם כל בית בתמורה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle S} זוכה לביקור על ידי האינדקסים $i,j$ אינו אחיד.
קיימת התנגשות בין מפתחות, שני מפתחות שמפיקים מצב פנימי זהה, ובגלל זה מפתחות הצפנה סודיים שונים יפיקו זרם מפתח זהה (Matsui).
קיימת מחלקה עצומה של מפתחות חלשים^[11]^[12], כך שבידיעת חלק קטן מהמפתח הסודי אפשר לנחש בתים רבים של פלט זרם המפתח. Mironov ניתח כמה בתים מהפלט הראשוני של זרם המפתח סובלים מהטייה והמליץ להיפטר מ-512 הבתים הראשונים.

המצב הפנימי

פורסמו מספר התקפות^[13]^[14]^[15]^[16] לשחזור המצב הפנימי של הצופן מתוך מצב פנימי ידוע. וכן שחזור מפתח ההצפנה מתוך המצב הפנימי.
אם סיבוכיות שחזור המפתח הסודי מתוך מהתמורה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle S} נמוכה משחזור התמורה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle S} מתוך זרם המפתח, אפשר לשלב את שתיהן יחד להתקפה מוצלחת יותר.
מקסימוב וחוברטוביץ' פיתחו התקפה תאורטית^[17] לשחזור המצב הפנימי בסיבוכיות של הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2^{241}} זמן וזרם מפתח. Golić ו-Morgari פיתחו אלגוריתם הסתברותי^[18] לשחזור המצב הפנימי מתוך זרם המפתח באורך הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2^{41}} בזמן של הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2^{689}} .

מחולל זרם המפתח PRGA

התגלו מצבים פנימיים שלעולם לא יופיעו בזרם המפתח (Finney).
משפט Glimpse מראה שקיימת "דליפה" של מידע בבתי זרם המפתח (Jenkins). בניגוד לצפוי ממחרוזת אקראית באורך הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} , ההסתברות לניחוש בתים אחדים מהמפתח מתוך בתים של המצב היא הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2/N} .
בפלט המפתח קיימים שני סוגים של הטיה; הטיה קצרת-טווח והטיה ארוכת-טווח. כלומר קיימת חולשה (חוסר אקראיות) מובנית בבתי זרם המפתח, במיוחד בבתים הראשונים (למשל הבית השני שסובל מהטיה חמורה). אפשר להימנע מההטייה קצרת הטווח אם נפטרים מ-512 הבתים הראשונים כפי שהומלץ וייושם בחלק מהפרוטוקולים.
פותחו התקפות נגד RC4 אם וקטור אתחול כפי שנמצא בשימוש WEP^[19]^[20].

התקפת הבחנה

התקפת הבחנה (Distinguishing Attack) היא התקפה סטטיסטית על פלט מחולל זרם המפתח^[21]^[22]^[23]. במצב אידיאלי, זרם המפתח אמור להראות על פניו כרצף אקראי לכל דבר. כלומר לא ניתן יהיה להבדילו מרצף אקראי שנוצר ממחולל אקראי אמיתי. מחולל זרם המפתח של RC4 הוא לא יותר מאשר מחולל פסאודו-אקראי שמקבל גרעין התחלתי סודי שהוא המפתח "ומותח" אותו למחרוזת אקראית באורך רצוי. התקפת הבחנה מתמקדת במציאת הבדלים או ניתוח ההסתברות שסיבית 1 או 0 תופיע בפוזיציה מסוימת בהשוואה לזרם אקראי אמיתי. אלגוריתם הבחנה מקבל קלט באורך הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} בתים שמקורם יכול להיות מזרם המפתח או ממחולל אקראי אמיתי ותפקידו להחזיר תשובה לאיזה סוג מהם הוא משתייך. אם נמצאו הבדלים, עובדה זו כשלעצמה יכולה לפתוח פתח להתקפות ולשבירת הצופן.

מחקרים מוכיחים כי כלל העדכון של RC4 שהוא הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle j=j+S[i]} אינו בחירה טובה וקיימת בו חולשה מובנית.
מבדיקה סטטיסטית שעשו ב-2001 גילו שמיר, איציק מנטין ופלורר^[24]^[25] שהבתים הראשונים של זרם המפתח של צופן RC4 אינם אקראיים לגמרי ומדליפים מידע לגבי המפתח. נתון זה, אפשר להם לפתח התקפה יעילה כנגד WEP (מערכת אבטחה לרשת אלחוטית). בתחילת 2007 אף פורסמו דרכים חדשות לפיצוחה בזמן קצר מאד (פחות מדקה) תוך שימוש בכמות לא רבה של טקסט מוצפן. העובדה ש-WEP נפרצה הובילה ביוני 2004 לפיתוח תקן מחמיר יותר הקרוי IEEE 802.11i המשמש בסיס לדור השני באבטחת רשת סלולרית WPA (קיצור של Wi-Fi Protected Access). ב-2011 פורסמו^[26] מספר חולשות נוספות של הצופן. שיחד עם חולשות ידועות אחרות מאפשרות התקפה לשחזור מפתח ההצפנה בהינתן 9,800 חבילות מוצפנות בלבד.

למרות האמור מערכות רבות בעולם עדיין משתמשות בטכנולוגיה המיושנת בעיקר מסיבות של יעילות ולמרות אמצעי הזהירות שננקטים, מומחים מתריעים על כך שקיימות פרצות חמורות במערכות אלו וישנן אף כאלו שניתן לפרוץ אותן תוך מספר שניות.

גרסאות מתקדמות

למרות החולשות שהתגלו בצופן RC4, הוא אטרקטיבי בשל העובדה שהוא נוח ויעיל למימוש בתוכנה. הרוב סבורים שכדאי לעבור לצפני זרם חזקים יותר שנבדקו והתקבלו על ידי eSTREAM כמו HC-128. אילו צפני זרם הפועלים בדרך כלל ברמה של מילים בגודל 32 או 64 סיביות והם בטוחים יותר לשימוש, אם כי מעט מורכבים ליישום.

קיימים צפני זרם רבים שמנסים לחקות את המבנה של RC4. כלומר פרמוטציה פנימית גדולה שנקראת מצב (state) והיא מורכבת בדרך כלל ממערך אחד או יותר של הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} אלמנטים כל אחד בגודל הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} , מספר מוגבל של אינדקסים ופעולת חיבור מודולו הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} לעיתים בתוספת הזזה מעגלית (rotation). להלן כמה מהם: Py, Py6, IA, ISAAC, NGG, GGHN. חלקם הוצעו לפרויקט ECRYPT האירופאי. כל הצפנים המנויים לא עמדו במבחן קריפטואנליזה (התקפת הבחנה) ונפסלו^[27]. לעומתם קיימים מספר אלגוריתמים מבוססי RC4 ששרדו קריפטואנליזה, ביניהם ניתן למנות את: IBAA, Pypy, HC-256, VMPC.

באופן כללי היתרונות של צופן RC4 הם:

שימוש במערכים המאפשר זיכרון פנימי עצום במחיר מועט.
שימוש בפעולה פשוטה, חיבור מודולו הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} בלבד.
עיצוב פשוט ונקי (קל ליישום והטמעה).
לא ידוע על התקפה לשחזור המפתח הסודי מלבד כוח גס.

חסרונות:

פועל ברמה של בתים בלבד (מה שיכול להוות יתרון במקרים מסוימים), לא יעיל בארכיטקטורת 32 או 64 סיביות.
קיימות הטיות סטטסטיות בפלט המחולל לעומת זרם אקראי אמיתי (ידוע על התקפות הבחנה מוצלחות נגד הצופן).
שלב הכנת מפתח אינו אקראי (קיימת הטיה סטטיסטית חמורה בבתים הראשונים).

נעשו מספר מאמצים לתקן את הליקויים של צופן RC4 על מנת ליהנות מפשטותו הרבה מבלי להיחשף לחולשות האמורות. להלן ארבע גרסאות ידועות של אלגוריתם RC4 שהוצעו כתחליף למקורי וחלקן הוכחו כבטוחות יותר.

RC4A

RC4A^[28] הוצע ב-2004 על ידי Bart Preneel ו-Souradyuti Paul כחלופה לאלגוריתם המקורי. האלגוריתם מבצע פחות פעולות פר בית אחד ותומך במקביליות. אחת ההתקפות הידועות נגד RC4 היא התקפת הבחנה המבוססת על רמת מתאם גבוהה בין המצב הפנימי לפלט האלגוריתם. הפתרון שהוצע הוא לגרום לתלות נוספת של הפלט עם משתנים אקראיים נוספים, כך ההסתברות לניחוש מוצלח של בתי המצב הפנימי תוך התבוננות בפלט תהיה נמוכה יותר. על בסיס הרעיון הזה עוצב RC4A. הצופן הוא הרחבה של המחולל הפנימי PRGA של צופן RC4 בעוד שתהליך הכנת המפתח נותר ללא שינוי. לצורך כך משתמשים בשתי תמורות (מערכים) הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_1,S_2} במקום אחת וכן שני אינדקסים הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle j_1,j_2} במקום אחד. הכנת התמורות נעשית על ידי על ידי KSA של RC4 לעיל עם שני מפתחות סודיים שונים הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_1,k_2} (אחד יכול להיות מופק מהשני באמצעות פונקציה פסאודו-אקראית כלשהי כמו RC4). להלן תיאור האלגוריתם:

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Set: }i = 0, j_1=j_2=0}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{Loop:}}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle i = i + 1}
הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle j_1=j_1 + S_1[i]}
הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Swap}(S_1[i], S_1[j_1])}
${\text{Output: }}S_{2}[S_{1}[i]+S_{1}[j_{1}]]$
הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle j_2=j_2 + S_2[i]}
הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Swap}(S_2[i], S_2[j_2])}
הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Output: }S_1[S_2[i] + S_2[j_2]]}

בכל ריצה של המחולל הפנימי האינדקס הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} מקודם פעם אחת ונוצרים שני בתים של זרם מפתח, אחד מכל מערך. הפונקציה Swap מתוארת לעיל.

VMPC

הצופן Variably Modified Permutation Composition^[29] פותח ב-2004 על ידי Bartosz Zoltak והוצע כתחליף ל-RC4. הרעיון מבוסס על פונקציית פלט מורכבת יותר: הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle P[P[P[x]]+1]} . כאשר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle P} היא פרמוטציה, זאת במטרה להקשות על ניחוש וכן למנוע הטיות סטטיסטיות לא רצויות של זרם המחולל. אלגוריתם ההכנה מקבל מפתח הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle K} באורך הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle c} בתים וכן וקטור אתחול הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle V} באורך הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} בתים ומערבב את הפרמוטציה הראשונית בהתאם. פלט המחולל הפנימי הוא בית אחר בית עד למספר הבתים הרצוי הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle L} שהוא אורך המסר להצפנה בבתים.

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{VMPC \ KSA:}}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle s=0}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{For }i = 0\text{ to }255\text{ do: }P[n] = n}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{For }m = 0\text{ to }767\text{ do:}}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle n=m\text{ mod }256}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle s=P[(s+P[n]+K[m\text{ mod }c])\text{ mod }256]}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Swap}(P[n], P[s])}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{For }m = 0\text{ to }767\text{ do:}}

n=m{\text{ mod }}256

s=P[(s+P[n]+V[m{\text{ mod }}z]){\text{ mod }}256]

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Swap}(P[n], P[s])}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{VMPC \ PRGA:}}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle n = 0}

‎

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Repeat }L\text{ times:}}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle s = P[(s+P[n])\text{ mod }256}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Output: }P[(P[P[s]]+1)\text{ mod }256]}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Swap}(P[n], P[s])}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle n = (n+1)\text{ mod }256}

‎

RC4+‎

צופן RC4+‎^[30] הוצע ב-2008 על ידי Subhamoy Maitra ו-Goutam Paul כחלופה בטוחה לצופן RC4. הצופן משתמש בטכניקת ערבוב בשלוש שכבות שונות בשילוב עם וקטור איתחול. לאחר השינויים הצופן בטוח יותר אך לא קיימת הוכחה פורמלית לכך. המחקר בתחום יימשך וייתכנו גילויים חדשים. האלגוריתם הבא המקבל מפתח סודי ווקטור אתחול, שניהם באורך שרירותי ומפיק זרם מפתח באורך הרצוי. סימנים מוסכמים: הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \oplus} מייצג XOR וכן הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ll} מייצג הזזה (Shift) שמאלה, הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gg} מייצג הזזה ימינה, הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{0xAA}} קבוע הקסדצימלי (170 בייצוג עשרוני):

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{Initializing:}}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{For }i = 0\text{ to }N-1\text{ do: }S[i]=i}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle j=0}

‎

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{Layer \ 1: \ Basic \ Scrambling}}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{For }i = 0\text{ to }N-1\text{ do:}}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle j = j + S[i] + K[i]}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Swap}(S[i], S[j])}

‎

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{Layer \ 2: \ Scrambilng \ with \ IV}}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{For }i = N/2 - 1\text{ down to }0\text{ do:}}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle j = (j + S[i])\oplus(K[i] + IV[i])}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Swap}(S[i], S[j])}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{For }i = N/2\text{ to }N - 1\text{ do:}}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle j = (j + S[i])\oplus(K[i] + IV[i])}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Swap}(S[i], S[j])}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{Layer \ 3: \ Zigzag \ Scrambling}}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{For }y = 0\text{ to }N - 1\text{ do:}}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{If }y\equiv 0\text{ mod }2\text{ then: }i = y/2}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Else: }i = N - (y+1)/2}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle j = j + S[i] + K[i]}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Swap}(S[i], S[j])}

‎

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{PRGA+}}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle i = j = 0}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{Keystream \ Generation \ Loop:}}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle i = i + 1}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle j = j + S[i]}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Swap}(S[i], S[j])}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle t = S[i] + S[j]}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle u = (S[i\gg 3\ \oplus \ j\ll 5]+S[i\ll 5\ \oplus \ j\gg 3])\oplus\text{0xAA}}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Output: }(S[t]+S[u])\oplus S[j + S[j]]}

Spritz

Spritz^[31] הוא גרסה מתקדמת של RC4 שפותחה ב-2014 על ידי רונלד ריבסט ו-Jacob Schuldt. הצופן עוצב לפי פרדיגמת פונקציית ספוג שהיא מבנה קריפטוגרפי בטוח שיושם בפונקציית הגיבוב Keccak המאפשר הפעלת פרמוטציה פסאודו-אקראית לצורך פרימיטיבים קריפטוגרפיים שונים כמו הצפנה סימטרית, פונקציית גיבוב או אימות מסרים. מבנה הספוג מורכב ממצב פנימי גדול ושני שלבי הפעלה "ספיגה וסחיטה". פונקציית הספיגה מקבלת מפתח הצפנה ווקטור האתחול (אם יש) ומעדכנת את המצב הפנימי בהתאם, פונקציית הסחיטה מספקת זרם פסאודו-אקראי המשמש כמפתח. בצופן Spritz ארבעה מרכיבים עיקריים, איתחול (Init), ערבוב (Shuffle), ספיגה (Absorb) וסחיטה (Squeeze). לאחר אתחול תחילה סופגים את המפתח הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle K} על ידי ${\text{Absorb}}(K)$ ואז ההצפנה מתבצעת עם הפונקציית הסחיטה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Squeeze}(r)} המקבלת פרמטר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle r} "וסוחטת" מחרוזת פסאודו-אקראית באורך הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle r} בתים אותם מחברים עם המסר המקורי ב-XOR. הצופן עוצב כך שיוכל לתמוך בכל הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} אבל צריך להבטיח ש-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle w} יהיה זר ל-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} לשם כך הפונקציה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Whip(r)}} משתמשת ב-GCD. במקרה ש-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} הוא חזקה של 2 (כגון 256) מספיק שיהיה אי זוגי, לכן אפשר להחליף את הלולאה האחרונה בפונקציה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Whip(r)}} במשפט הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle w = w + 2} . וכן יש לזכור שכל פעולות החיבור הן מודולו הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle N} . להלן תיאור האלגוריתם:

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{InitializeState(N)}}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle i = j = k = z = a = 0}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle w = 1}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{For }v = 0\text{ to }N - 1\text{ do:}}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle S[v] = v}

‎

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{Absorb(I)}}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{For }v = 0\text{ to }I.length - 1}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{AbsorbByte}(I[v])}

‎

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{AbsorbByte(b)}}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{AbsorbNibble}(\text{low}(b))}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{AbsorbNibble}(\text{high}(b))}

‎

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{AbsorbNibble(x)}}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{If }a = \left\lfloor N/2\right\rfloor\text{ then Shuffle}()}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Swap}(S[a], S[\left\lfloor N/2\right\rfloor + x ])}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle a = a + 1}

‎

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{AbsorbStop()}}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{If }a = \left\lfloor N/2\right\rfloor\text{ then Shuffle}()}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle a = a + 1}

‎

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{Shuffle()}}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Whip}(2N)}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Crush}()}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Whip}(2N)}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Crush()}}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Whip}(2N)}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle a = 0}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{Whip(r)}}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{For }v = 0\text{ to }r - 1\text{ do: Update}()}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Do: }w = w + 1}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Until GCD}(w,N) = 1}

‎

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{Crush()}}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{For }v = 0\text{ to }\left\lfloor N/2\right\rfloor - 1\text{ do}}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{If }S[v] > S[N - 1 - v]}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Swap}(S[v], S[N - 1 - v])}

‎

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{Squeeze(r)}}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{If }a > 0\text{ then Shuffle}()}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle P =\text{ New Array}(r)}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{For }v = 0\text{ to }r - 1}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle P[v] = \text{Drip}()}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Return }P}

‎

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{Drip()}}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{If }a > 0\text{ then Shuffle}()}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Update}()}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Return Output}()}

‎

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{Update()}}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle i = i + w}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle j = k + S[j + S[i]]}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle k = i + k + S[j]}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Swap}(S[i], S[j])}

‎

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{Output()}}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle z = S[j + S[i + S[z + k]]]}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Return }z}

VMPC-R

אלגוריתם VMPC-R^[32] הוא שיפור של VMPC, שפותח על ידי Bartosz Zoltak ב-2004. הוא ניתח מספר אלגוריתמים בסגנון RC4 ומצא חולשות סטטיסטיות ברבים מהם כולל Spritz. הוא מצא שבצופן Spritz של ריבסט ושולדט עבור הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle N=8} ההסתברות ש-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Output}(x)=\text{Output}(x+2)} היא הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1/N+0.000498} . ההטיה נעשית משמעותית לאחר כמות של הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2^{21.9}} פלטים. כמו כן מצא הטיות סטיסטיות גם במקרה של הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle N=16} . הוא פיתח לצורך הבדיקה מבחן סטטיסטי חדש שנקרא distant-equalities שבו בודקים את מספר המופעים של האירועים הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_i=z_{i+k}} עבור הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle k\in\{1,2,...,8\}} ביחס לצפוי מזרם אקראי אמיתי. אירוע הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} פירושו ששני מילים במרחק הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle k} זה מזה זהים. לאור חולשות שהתגלו ב-VMPC על ידי מקסימוב^[33], פיתח Bartosz Zoltak ב-2013 את הגרסה המשופרת של הצופן לה הוסיף את האות R (ראנדום). לטענתו היא הטובה ביותר האפשרית בסגנון RC4 והפלט שלה עומד בכל המבחנים הסטטיסטיים הידועים. אם כי קצת איטית בהשוואה ל-RC4 המקורי. להלן תיאור האלגוריתם המקבל וקטור אתחול ומפתח הצפנה ומפיק בית אחר בית של מחרוזת פסאודו-אקראית:

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle N\text{ word size e.g. }N=256} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle a,b,c,d,e,f,n\text{ are integer variables}} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle P,S\text{ are N-element permutations}} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle +\text{ denotes addition modulo }N} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle K\text{ array of }k\text{ integers; }k\in\{1,...,N\}} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle V\text{ an IV array of }v\text{ elements }v\in\{1,...,N\}} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R=\left\lceil k^2/(6N)\right\rceil\cdot N} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\text{ is a temprorary counter}} ‎ הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{VMPC}\text{-}\mathbf{R \ KSA}} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle a=b=c=d=e=f=n=0} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{For }i=0\text{ to }N-1\text{ do}} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle P[i]=S[i]=i} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{KsaRound}(K,k)} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{KsaRound}(V,v)} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{KsaRound}(K,k)} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle n=S[S[S[c+d]]+1]} ‎ ‎ ‎ ‎ ‎ ‎ ‎	הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{KsaRound}(M,m)} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle i=0} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Repeat R times:}} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle a=P[a+f+M[i]]+i; \ \ i=(i+1)\text{ mod }m} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle b=P[b+a+M[i]]+i; \ \ i=(i+1)\text{ mod }m} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle c=P[c+b+M[i]]+i; \ \ i=(i+1)\text{ mod }m} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle d=P[d+c+M[i]]+i; \ \ i=(i+1)\text{ mod }m} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle e=P[e+d+M[i]]+i; \ \ i=(i+1)\text{ mod }m} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle f=P[f+e+M[i]]+i; \ \ i=(i+1)\text{ mod }m} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Swap}(P[n],P[b]), \ \text{Swap}(S[n],S[e])} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Swap}(P[d],P[f]), \ \text{Swap}(S[a],S[c])} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle n=n+1} ‎ הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{VMPC}\text{-}\mathbf{R \ PRNG}} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Loop:}} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle a=P[a+c+S[n]], \ b=P[b+a], \ c=P[c+b]} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle d=S[d+f+P[n]], \ e=S[e+d], \ f=S[f+e]} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \boldsymbol{\mathbf{Output:}\ S[S[S[c+d]]+1]}} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Swap}(P[n],P[f])} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Swap}(S[n],S[a])} הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle n=n+1}

קישורים חיצוניים

התקפה מעשית כנגד RC4 של איצק מנטין ועדי שמיר
נקודות תורפה באלגוריתם תיזמון מפתח של RC4, פלורר, מנטין ושמיר מכון ויצמן למדע, 2001
Using the Fluhrer, Mantin, and Shamir Attack to Break WEP, Stubblefield, Loannidis, and Rubin, מעבדות AT&T
פריצת WEP 104 bit בפחות מדקה

הערות שוליים

^ M. Akgun, P. Kavak and H. Demirci. New Results on the Key Scheduling Algorithm of RC4. Indocrypt 2008. A sketch of this work has been presented in Eurocrypt 2008 Rump Session, available at http://www.iacr.org/conferences/eurocrypt2008v/index.html [last accessed on July 18, 2008].
^ A. Roos. A class of weak keys in the RC4 stream cipher. 1995.
^ L. R. Knudsen, W. Meier, B. Preneel, V. Rijmen and S. Verdoolaege. Analysis Methods for (Alleged) RCA. ASIACRYPT 1998, pages 327-341, vol. 1514, Lecture Notes in Computer Science, Springer-Verlag.
^ S. R. Fluhrer and D. A. McGrew. Statistical Analysis of the Alleged RC4 Keystream Generator. FSE 2000, pages 19-30, vol. 1978, Lecture Notes in Computer Science, Springer-Verlag.
^ S. Maitra and G. Paul. New Form of Permutation Bias and Secret Key Leakage in Keystream Bytes of RC4. FSE 2008, pages 253-269, vol. 5086, Lecture Notes in Computer Science, Springer Berlin / Heidelberg.
^ G. Paul, S. Rathi and S. Maitra. On Non-negligible Bias of the First Output Byte of RC4 towards the First Three Bytes of the Secret Key. Proceedings of the International Workshop on Coding and Cryptography (WCC) 2007, pages 285-294. To appear in Designs, Codes and Cryptography, special issue of in memory of Hans Dobbertin, DOI 10.1007/s10623-008-9177-7.
^ G. Paul and S. Maitra. Permutation after RC4 Key Scheduling Reveals the Secret Key. SAC 2007, pages 360-377, vol. 4876, Lecture Notes in Computer Science, Springer Berlin / Heidelberg.
^ G. Paul, S. Maitra and R. Srivastava. On Non-Randomness of the Permutation after RC4 Key Scheduling. Applied Algebra, Algebraic Algorithms, and Error Correcting Codes (AAECC) 2007, pages 100-109, vol. 4851, Lecture Notes in Computer Science, Springer Berlin / Heidelberg.
^ S. Paul and B. Preneel. A New Weakness in the RC4 Keystream Generator and an Approach to Improve the Security of the Cipher. FSE 2004, pages 245-259, vol. 3017, Lecture Notes in Computer Science, Springer-Verlag.
^ I. Mantin. Analysis of the stream cipher RC4. Master’s Thesis, The Weizmann Institute of Science, Israel, 2001.
^ D. Wagner. My RC4 weak keys. 26 September, 1995.
^ S. R. Fluhrer, I. Mantin and A. Shamir. Weaknesses in the Key Scheduling Algorithm of RC4. SAC 2001, pages 1-24, vol. 2259, Lecture Notes in Computer Science, Springer-Verlag.
^ E. Biham and Y. Carmeli. Efficient Reconstruction of RC4 Keys from Internal States. FSE 2008, pages 270-288, vol. 5086, Lecture Notes in Computer Science, Springer Berlin / Heidelberg.
^ G. Paul and S. Maitra. RC4 State Information at Any Stage Reveals the Secret Key. IACR Eprint Server, eprint.iacr.org, number 2007/208, June 1, 2007.
^ V. Tomasevic, S. Bojanic and O. Nieto-Taladriz. Finding an internal state of RC4 stream cipher. Information Sciences, pages 1715-1727, vol. 177, 2007.
^ S. Paul and B. Preneel. Analysis of Non-fortuitous Predictive States of the RC4 Keystream Generator. IN-DOCRYPT 2003, pages 52-67, vol. 2904, Lecture Notes in Computer Science, Springer-Verlag.
^ A. Maximov and D. Khovratovich. New State Recovering Attack on RC4 (Full Version). IACR Eprint Server, eprint.iacr.org, number 2008/017, Jan 10, 2008. (To Appear in Crypto 2008 under the title "New State Recovery Attack on RC4").
^ J. Golic. Linear statistical weakness of alleged RC4 keystream generator. EUROCRYPT 1997, pages 226-238, vol. 1233, Computer Science, SpringLecture Notes in er-Verlag.
^ A. Stubblefield, J. Ioannidis and A. D. Rubin. Using the Fluhrer, Mantin, and Shamir Attack to Break WEP. AT&T Labs Technical Report TD-4ZCPZZ, August 6, 2001.
^ E. Tews, R. P. Weinmann and A. Pyshkin. Breaking 104 bit WEP in less than 60 seconds. IACR Eprint Server, eprint.iacr.org, number 2007/120, April 1, 2007 [last accessed on July 18, 2008].
^ I. Mantin. Predicting and Distinguishing Attacks on RC4 Keystream Generator. EUROCRYPT 2005, pages 491-506, vol. 3494, Lecture Notes in Computer Science, Springer-Verlag.
^ Y. Tsunoo, T. Saito, H. Kubo and T. Suzaki. A Distinguishing Attack on a Fast Software-Implemented RC4-Like Stream Cipher. IEEE Transactions on Information Theory, page 3250-3255, vol. 53, issue 9, September 2007.
^ S. Vaudenay and M. Vuagnoux. Passive-Only Key Recovery Attacks on RC4. SAC 2007, pages 344-359, vol. 4876, Lecture Notes in Computer Science, Springer Berlin / Heidelberg.
^ I. Mantin and A. Shamir. A Practical Attack on Broadcast RC4. FSE 2001, pages 152-164, vol. 2355, Lecture Notes in Computer Science, Springer-Verlag.
^ I. Mantin. A Practical Attack on the Fixed RC4 in the WEP Mode. ASIACRYPT 2005, pages 395-411, volume 3788, Lecture Notes in Computer Science, Springer-Verlag.
^ Discovery and Exploitation of New Biases in RC4
^ On the (In)security of Stream Ciphers Based on Arrays and Modular Addition
^ A New Weakness in the RC4 Keystream Generator and an Approach to Improve the Security of the Cipher*
^ VMPC One-Way Function and Stream Cipher
^ Analysis of RC4 and Proposal of Additional Layers for Better Security Margin
^ Spritz - a spongy RC4-like stream cipher and hash function
^ VMPC-R Cryptographically Secure Pseudo-Random Number Generator Alternative to RC4
^ Alexander Maximov: Two Linear Distinguishing Attacks on VMPC and RC4A and Weakness of RC4 Family of Stream Ciphers. Proceedings of FSE 2005, LNCS, vol. 3557, Springer-Verlag, 2005, pages 342-358

[1] M. Akgun, P. Kavak and H. Demirci. New Results on the Key Scheduling Algorithm of RC4. Indocrypt 2008. A sketch of this work has been presented in Eurocrypt 2008 Rump Session, available at http://www.iacr.org/conferences/eurocrypt2008v/index.html [last accessed on July 18, 2008].

[2] A. Roos. A class of weak keys in the RC4 stream cipher. 1995.

[3] L. R. Knudsen, W. Meier, B. Preneel, V. Rijmen and S. Verdoolaege. Analysis Methods for (Alleged) RCA. ASIACRYPT 1998, pages 327-341, vol. 1514, Lecture Notes in Computer Science, Springer-Verlag.

[4] S. R. Fluhrer and D. A. McGrew. Statistical Analysis of the Alleged RC4 Keystream Generator. FSE 2000, pages 19-30, vol. 1978, Lecture Notes in Computer Science, Springer-Verlag.

[5] S. Maitra and G. Paul. New Form of Permutation Bias and Secret Key Leakage in Keystream Bytes of RC4. FSE 2008, pages 253-269, vol. 5086, Lecture Notes in Computer Science, Springer Berlin / Heidelberg.

[6] G. Paul, S. Rathi and S. Maitra. On Non-negligible Bias of the First Output Byte of RC4 towards the First Three Bytes of the Secret Key. Proceedings of the International Workshop on Coding and Cryptography (WCC) 2007, pages 285-294. To appear in Designs, Codes and Cryptography, special issue of in memory of Hans Dobbertin, DOI 10.1007/s10623-008-9177-7.

[7] G. Paul and S. Maitra. Permutation after RC4 Key Scheduling Reveals the Secret Key. SAC 2007, pages 360-377, vol. 4876, Lecture Notes in Computer Science, Springer Berlin / Heidelberg.

[8] G. Paul, S. Maitra and R. Srivastava. On Non-Randomness of the Permutation after RC4 Key Scheduling. Applied Algebra, Algebraic Algorithms, and Error Correcting Codes (AAECC) 2007, pages 100-109, vol. 4851, Lecture Notes in Computer Science, Springer Berlin / Heidelberg.

[9] S. Paul and B. Preneel. A New Weakness in the RC4 Keystream Generator and an Approach to Improve the Security of the Cipher. FSE 2004, pages 245-259, vol. 3017, Lecture Notes in Computer Science, Springer-Verlag.

[10] I. Mantin. Analysis of the stream cipher RC4. Master’s Thesis, The Weizmann Institute of Science, Israel, 2001.

[11] D. Wagner. My RC4 weak keys. 26 September, 1995.

[12] S. R. Fluhrer, I. Mantin and A. Shamir. Weaknesses in the Key Scheduling Algorithm of RC4. SAC 2001, pages 1-24, vol. 2259, Lecture Notes in Computer Science, Springer-Verlag.

[13] E. Biham and Y. Carmeli. Efficient Reconstruction of RC4 Keys from Internal States. FSE 2008, pages 270-288, vol. 5086, Lecture Notes in Computer Science, Springer Berlin / Heidelberg.

[14] G. Paul and S. Maitra. RC4 State Information at Any Stage Reveals the Secret Key. IACR Eprint Server, eprint.iacr.org, number 2007/208, June 1, 2007.

[15] V. Tomasevic, S. Bojanic and O. Nieto-Taladriz. Finding an internal state of RC4 stream cipher. Information Sciences, pages 1715-1727, vol. 177, 2007.

[16] S. Paul and B. Preneel. Analysis of Non-fortuitous Predictive States of the RC4 Keystream Generator. IN-DOCRYPT 2003, pages 52-67, vol. 2904, Lecture Notes in Computer Science, Springer-Verlag.

[17] A. Maximov and D. Khovratovich. New State Recovering Attack on RC4 (Full Version). IACR Eprint Server, eprint.iacr.org, number 2008/017, Jan 10, 2008. (To Appear in Crypto 2008 under the title "New State Recovery Attack on RC4").

[18] J. Golic. Linear statistical weakness of alleged RC4 keystream generator. EUROCRYPT 1997, pages 226-238, vol. 1233, Computer Science, SpringLecture Notes in er-Verlag.

[19] A. Stubblefield, J. Ioannidis and A. D. Rubin. Using the Fluhrer, Mantin, and Shamir Attack to Break WEP. AT&T Labs Technical Report TD-4ZCPZZ, August 6, 2001.

[20] E. Tews, R. P. Weinmann and A. Pyshkin. Breaking 104 bit WEP in less than 60 seconds. IACR Eprint Server, eprint.iacr.org, number 2007/120, April 1, 2007 [last accessed on July 18, 2008].

[21] I. Mantin. Predicting and Distinguishing Attacks on RC4 Keystream Generator. EUROCRYPT 2005, pages 491-506, vol. 3494, Lecture Notes in Computer Science, Springer-Verlag.

[22] Y. Tsunoo, T. Saito, H. Kubo and T. Suzaki. A Distinguishing Attack on a Fast Software-Implemented RC4-Like Stream Cipher. IEEE Transactions on Information Theory, page 3250-3255, vol. 53, issue 9, September 2007.

[23] S. Vaudenay and M. Vuagnoux. Passive-Only Key Recovery Attacks on RC4. SAC 2007, pages 344-359, vol. 4876, Lecture Notes in Computer Science, Springer Berlin / Heidelberg.

[24] I. Mantin and A. Shamir. A Practical Attack on Broadcast RC4. FSE 2001, pages 152-164, vol. 2355, Lecture Notes in Computer Science, Springer-Verlag.

[25] I. Mantin. A Practical Attack on the Fixed RC4 in the WEP Mode. ASIACRYPT 2005, pages 395-411, volume 3788, Lecture Notes in Computer Science, Springer-Verlag.

[26] Discovery and Exploitation of New Biases in RC4

[27] On the (In)security of Stream Ciphers Based on Arrays and Modular Addition

[28] A New Weakness in the RC4 Keystream Generator and an Approach to Improve the Security of the Cipher*

[29] VMPC One-Way Function and Stream Cipher

[30] Analysis of RC4 and Proposal of Additional Layers for Better Security Margin

[31] Spritz - a spongy RC4-like stream cipher and hash function

[32] VMPC-R Cryptographically Secure Pseudo-Random Number Generator Alternative to RC4

[33] Alexander Maximov: Two Linear Distinguishing Attacks on VMPC and RC4A and Weakness of RC4 Family of Stream Ciphers. Proceedings of FSE 2005, LNCS, vol. 3557, Springer-Verlag, 2005, pages 342-358

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

RC4

תוכן עניינים

הליך ההצפנה

יישומים

בטחון

KSA תהליך הכנת זרם המפתח

המצב הפנימי

מחולל זרם המפתח PRGA

התקפת הבחנה

גרסאות מתקדמות

RC4A

VMPC

RC4+‎

Spritz

VMPC-R

קישורים חיצוניים

הערות שוליים

תפריט ניווט

RC4

הליך ההצפנה

יישומים

בטחון

KSA תהליך הכנת זרם המפתח

המצב הפנימי

מחולל זרם המפתח PRGA

התקפת הבחנה

גרסאות מתקדמות

RC4A

VMPC

RC4+‎

Spritz

VMPC-R

קישורים חיצוניים

הערות שוליים

תפריט ניווט

חיפוש