KeeLoq

בקריפטוגרפיה, Keeloq הוא צופן בלוקים קנייני מבוסס חומרה המשתמש באוגר זיזה ממושב לא-ליניארי. פותח על ידי Frederick Bruwer ו-Willem Smit מחברת Nanoteq עם Gideon Kuhn מאוניברסיטת פרטוריה דרום אפריקה, נמכר ב-1995 לחברת Microchip ונרשם כפטנט בארצות הברית ב-1996.

שבב HCS301 שהוא חלק ממנגנון נעילה אלקטרוני של רכב, המכיל בתוכו את צופן KeeLoq

הצופן נמצא בשימוש במערכות בקרת נעילה מרחוק (ללא מפתח), חלק מטכנולוגיית hopping code (קוד מדלג למניעת שידור חוזר) בהתקנים כמו NTQ, HCS ו-PIC. הצופן היה ובגלל תאימות לאחור עדיין נמצא בשימוש נפוץ בתעשיית הרכב כחלק ממנגנון נעילה אלקטרוני של הרכב, ביניהם קרייזלר, טויוטה, וולוו ועוד רבים.

טרנסקודר KeeLoq

טרנסקודר טיפוסי כמו זה המופיע בתמונה משמאל פועל על עיקרון הנקרא קוד מקפץ או קוד מדלג המשתנה בכל הפעלה של המכשיר כמו סיסמה חד-פעמית. כדי למנוע מהגנב מלהקליט את האות המשודר על ידי השלט ושימוש חוזר בו לאחר מכן, המקודד משדר קוד שחרור נעילה מוצפן ואז משנה את הקוד להעפלה הבאה ומסתנכרן עם מנגנון הנעילה של הרכב בצורה בטוחה. מקודד Keeloq משתמש במפתח הצפנה הצרוב בתוך השבב עם צופן Keeloq כדי לפענח את הבלוק המשודר המכיל את קוד השחרור הטרי. הקוד משולב ב-XOR עם וקטור אתחול באורך 32 סיביות המופק מגרעין אקראי או מקוד קבוע שניתן לשינוי חיצוני בזמן "הלמידה" של המכשיר.

ב-1996 הוסיפה חברת Microchip טרנסקודר משודרג הנקרא HCS410 KEELOQ שכולל מספר שיפורים ביניהם שידור ארוך יותר של 67 סיביות וגרעין התחלתי באורך 60 סיביות ו-CRC. כמו כן כל המידע הסודי נצרב בשבב EEPROM באופן כזה שלא ניתן לקריאה חיצונית. שבב יותר חדש המכיל גם את KeeLoq לצורך תאימות עם מערכות ישנות הוא PIC12 ו-PIC16 בטכנולוגיית זיכרון הבזק.

תיאור כללי

Keeloq הוא צופן בלוקים איטרטיבי במבנה רשת פייסטל בלתי מאוזנת, בסגנון ייחודי המיישם מוטיבים מצופן זרם. הפונקציה הפנימית מפיקה סיבית אחת בכל סבב וכתוצאה מכך רק סיבית אחת של המצב הפנימי מתעדכנת בסבב אחד. באופן אחר אפשר לראות בפונקציה הפנימית כאוגר זיזה ממושב אי-ליניארי (בקיצור NLFSR) שבו הסיבית החדשה מחושבת בכל פעימה על ידי פונקציה בוליאנית אי-ליניארית המחוברת ב-XOR עם סיבית אחת מהמפתח. הצופן מקבל מפתח הצפנה באורך 64 סיביות ומצפין איתו בלוק טקסט גלוי באורך 32 סיביות ב-528 מהלכים. ההצפנה היא מחזורית עם מחזוריות באורך של 64 סיביות. היות ש-528 אינו מתחלק ב-64 למעשה המחזוריות נקטעת ב-16 הסבבים האחרונים. הסיבה לבחירה זו היא כדי לסכל התקפה אלגברית. הוכח ששיטה זו אינה מועילה לגמרי ויש דרכים ליישם התקפה אלגברית בשילוב עם התקפת גלישה נגד Keeloq. כל סיבית מפתח נפקדת בדיוק שמונה פעמים למעט 16 הסיביות הראשונות שבהן הצופן משתמש 9 פעמים. המשמעות היא שאחת ל-64 סבבים משתמשים באותה סיבית מפתח. במילים אחרות בסבבים $i,i+64,i+128,...$ תכולת אוגר המפתח זהה.

תרשים צופן KeeLoq

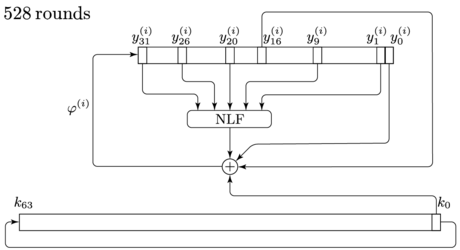
פירוט מהלכי הצופן

הצופן מכיל שני אוגרים ממושבים, האחד אוגר טקסט באורך 32 סיביות לתוכו נטען הטקסט המיועד להצפנה והשני אוגר מפתח באורך 64 סיביות שתפקידו להפיק סיביות להצפנת הטקסט בכל פעימה. אוגר המפתח מבצע הזזה מעגלית סיבית אחת בכל פעימה והסיבית $k_{0}$ נלקחת לפונקציית המשוב. תהי NLF פונקציה בוליאנית אי-ליניארית המקבלת חמישה משתנים בגודל סיבית אחת ומחזירה סיבית אחת (מפורטת בהמשך). עדכון סיבית המשוב הבאה $\varphi$ הוא חיבור XOR של תוצאת ה-NLF עם שתי הסיביות: $y_{0}^{(i)}$ ו-$y_{16}^{(i)}$ מתוך אוגר הטקסט וסיבית ההצפנה הבאה $k_{0}$ מתוך אוגר המפתח. יהיו$Y^{(i)}=(y_{31}^{(i)},...,y_{0}^{(i)})\in \{0,1\}^{32},y_{j}^{(i)}\in GF(2)$ תיאור המצב הפנימי של אוגר הטקסט במחזור $i$ כאשר $j=0,...,31$ וכן $K^{(i)}=(k_{63}^{(i)},...,k_{0}^{(i)})\in \{0,1\}^{32},k_{j}^{(i)}\in GF(2)$ מצב אוגר המפתח במחזור $i$ כאשר $j=0,...,63$ אז המהלכים הבאים מתרחשים בכל פעימה:

• חישוב סיבית המשוב: $\varphi ={\text{NLF}}\left(y_{31}^{(i)},y_{26}^{(i)},y_{20}^{(i)},y_{9}^{(i)},y_{1}^{(i)}\right)\oplus y_{16}^{(i)}\oplus y_{0}^{(i)}\oplus k_{0}^{(i)}$.
• הזזה ועדכון סיבית המשוב הבאה: $R^{(i+1)}=\left(\varphi ,y_{32}^{(i)},...,y_{1}^{(i)}\right)$.
• הזזה מעגלית של המפתח: $K^{(i+1)}=\left(k_{0}^{(i)},k_{63}^{(i)},...,k_{1}^{(i)}\right)$.

הצפנה

להצפנה תחילה טוענים את 64 סיביות מפתח ההצפנה לתוך אוגר המפתח $K=(k_{63},...,k_{0})\in \{0,1\}^{64},k_{j}\in GF(2)$ כאשר $j=0,...,63$ בהעתקה ישירה סיבית אחר סיבית. בלוק הטקסט הגלוי המיועד להצפנה $X=(x_{31},...,x_{0})\in \{0,1\}^{32},x_{j}\in GF(2)$ כאשר $j=0,...,31$ מועתק לתוך האוגר $Y^{(0)}=(x_{31},...,x_{0})$ ואז הטקסט המוצפן הוא $Z=(z_{31},...,z_{0})=Y^{(528)}\in \{0,1\}^{32},z_{j}\in GF(2)$ כאשר $j=0,...,31$.בניסוח אחר הטקסט המוצפן הוא תכולת אוגר הטקסט לאחר 528 פעימות בהן מבוצעים המהלכים המתוארים.

פענוח

לפענוח טוענים את אוגר המפתח באותה דרך בדיוק. פעולת הפענוח היא הפעולה ההפוכה של ההצפנה. בכל פעימה מתבצע:

• חישוב סיבית המשוב: $\varphi ={\text{NLF}}\left(y_{30}^{(i)},y_{25}^{(i)},y_{19}^{(i)},y_{8}^{(i)},y_{0}^{(i)}\right)\oplus y_{15}^{(i)}\oplus y_{31}^{(i)}\oplus k_{15}^{(i)}$.
• הזזה ועדכון הסיבית הבאה: $R^{(i+1)}=\left(y_{30}^{(i)},...,y_{0}^{(i)},\varphi \right)$.
• הזזה מעגלית של אוגר המפתח: $K^{(i+1)}=\left(k_{62}^{(i)},...,k_{0}^{(i)},k_{63}^{(i)}\right)$.

הטקסט המוצפן והטקסט המפוענח מחושבים בדרך דומה לאחר 528 פעימות.

פונקציית המשוב

פונקציית המשוב או פונקציית העדכון השוכנת בלב האלגוריתם היא פונקציה בוליאנית אי-ליניארית ממעלה 3 בעלת צורה אלגברית נורמלית (ANF) המקבלת חמשה משתנים (סיביות) ומחזירה סיבית אחת:

${\text{NLF}}(a,b,c,d,e)=d\oplus e\oplus ac\oplus ae\oplus bc\oplus be\oplus cd\oplus de\oplus ade\oplus ace\oplus abd\oplus abc$

מעל השדה $GF(2)$. הביטוי $ac$ פירושו כפל מודולו 2 של $a$ עם $c$ או בסימון מתמטי: $a\land c$, הסימן $\land$ נקרא (וגם). בחומרה אפשר ליישם פונקציה זו באמצעות מרבב.

דרך אחרת להציג אותה היא הפונקציה האי-ליניארית ${\text{0x3AC742E}}$ בבסיס הקסדצימלי. הכוונה היא שפלט הפונקציה ${\text{NLF}}(a,b,c,d,e)$ הוא הסיבית ה-$i$ של הקבוע ההקסדצימלי בכתיבה בינארית (מצד ימין כשהספירה מתחילה מאפס), כאשר $i=16a+8b+4c+2d+e$. לדוגמה ${\text{NLF}}(0,1,1,0,1)=1$ כי $i=8+4+1=13$ והסיבית ה-14 של ${\text{0x3AC742E}}$ היא 1.

דרך אחרת לתאר את פונקציית המשוב. אם נסמן את הסיבית הראשונה (LSB) של אוגר הטקסט $Y$ בסוף סבב ה-$i$ כ-$Y_{i}$, כאשר המצב הראשוני לפני תחילת פעולת הצופן נקרא סבב אפס. בסיום הסבב ה-528 הסיבית הראשונה נקראת $Y_{528}$, יתרת סיביות אוגר הטקסט מסומנות $Y_{529},Y_{530},...,Y_{559}$, כשהסיבית $Y_{559}$ היא המשמעותית ביותר (MSB). אם כן, הנוסחה הבאה נותנת את סיבית המשוב הבאה של אוגר הטקסט:

$Y_{i+32}={\text{NLF}}(Y_{i+31},Y_{i+26},Y_{i+20},Y_{i+9},Y_{i+1})\oplus K_{(i{\text{ mod }}64)}\oplus Y_{i}\oplus Y_{i+16}$

קריפטואנליזה

לטענת המפתחים צופן KeeLoq אמור לספק בטחון ברמה של DES. טענה שאינה נכונה. ב-2007 אנדריי בוגדנוב השתמש בהתקפת גלישה (slide attack) וקירוב ליניארי נגד keeLoq כדי לשבור את הצופן בסיבוכיות של $2^{37}$ הצפנות ו-$2^{32}$ בלוקים גלויים. Nicolas Courtois השתמש בטכניקת גלישה דומה בהתקפה אלגברית נגד גרסה מלאה במלוא הסבבים של הצופן בסיבוכיות של $2^{53}$ הצפנות עם $2^{16}$ בלוקים גלויים. שתי ההתקפות הללו אינן מעשיות ולא מהוות איום של ממש נגד הצופן בצורה בה הוא נמצא בשימוש כי מעשית לא ברור איך אפשר להשיג כמות כזו של טקסטים (שידורים) הדרושה להתקפה. בכל אופן הוכח שביטחונו אינו משתווה לזה של DES ולכן לא מומלץ להשתמש בו להצפנה כללית. בכל הגרסאות של המכשירים שעשו שימוש בצופן, הוגבל מפתח ההצפנה (חלק מסיביות המפתח אופסו בכוונה) מה שגורם לכך שדווקא התקפת כוח גס נחשבת יעילה. ב-2007 קבוצת חוקרים מהטכניון, האוניברסיטה העברית ואוניברסיטת לוון בראשות אלי ביהם, אור דונקלמן ו- Bart Preneel הצליחו בתקיפת היפגשות באמצע נגד KeeLoq בהסתמך על פרטים של האלגוריתם שדלפו לרשת ב-2006. ההתקפה שלהם היא התקפת גלוי-ידוע בשילוב התקפת הגלישה עם $2^{16}$ בלוקים ידועים בסיבוכיות של $2^{44.5}$ הצפנות והיא כמעט מעשית. ביישום ההתקפה בפועל צריך להאזין במשך 65 דקות לתקשורת עם השבב כדי להשיג את המידע הדרוש לצורך ההתקפה ובין 7.8 ל-3.4 ימים כדי לבצע את ההתקפה על מעבד 64 ביט. הגרסה שעושה שימוש בגרעין באורך 60 סיביות ניתנת לשבירה בתוך כ-100 ימים בכוח גס מקבילי על שבב ייעודי אך רוב המימושים המעשיים של הצופן בשבבים הישנים משתמשים בגרעין קצר.

התקפת ערוץ צדדי

ערך מורחב – התקפת ערוץ צדדי

ב-2008 הצליחו חוקרים מאוניברסיטת רוהר בוכום לשבור את הצופן לחלוטין בהתקפת ערוץ צדדי שהיא סוג של התקפת צריכה דיפרנציאלית. ההתקפה שלהם מצליחה נגד כל המימושים של הצופן בין היתר כחלק מטכנולוגיית RFID. הרעיון הוא מדידת צריכת החשמל של המכשיר בזמן השימוש בצופן ועם מידע זה חילוץ "מפתח יצרן" שהוא מפתח סודי המוטמע בשבב איתו משתמשים ליצירת מפתחות אחרים. ההשלכות של התקפה זו הרסניות במיוחד כי על ידי ציתות לשני שידורים בלבד ממרחק של כמאה מטר המתקיף יכול לשכפל כל התקן לגיטימי שבו מוטמע מפתח יצרן זהה.

התקפת שידור חוזר

הקוד המדלג אינו משתמש בערכים אקראיים חד פעמיים בכל שידור לכן מעצם טבעו חשוף להתקפת שידור חוזר. לא ניתן להוסיף חותם זמן כיוון שיש חשש לאי תאימות בין השעונים. לכן אם גנב מצליח לשבש את השידור בזמן פעולת השלט וליירט את התשדורת יעלה בידו להשיג קוד שחרור נעילה טרי שטרם נעשה בו שימוש ולכן ייתכן שיהיה ניתן להשתמש בו מאוחר יותר כדי לפתוח את הרכב. הסיבה היא כי אם המשתמש לחץ על הכפתור בשלט מחוץ לטווח הקליטה שלו פחות מ-16 פעמים הטרנסקודר לא יאבד סינכרון כל עוד המונה טרי (שלא התקבל קודם לכן). למעשה, ב-2015 פרסם האקר בשם Samy Kamkar ב-DEF CON 23 תיאור של מכשיר פשוט בגודל ארנק שאיתו אפשר לגנוב קוד שחרור נעילה של דלת רכב, מוסך, חניון או כל דלת אלקטרונית המבוקרת עם שבב דומה. הרעיון הוא שהמכשיר משדר קוד שיבוש בזמן שבעלי השלט מנסים להפעיל אותו, באותו זמן המכשיר גם מקליט את השידור. בעקבות הניסיון הראשון שנכשל עקב השיבוש בעלי השלט מנסים שוב. לאחר שני ניסיונות מתקבלים אצל הגנב שני קודי שחרור כאשר הקוד ראשון משודר לרכב בדיוק בזמן שבעלי השלט מנסים בפעם שנייה (היות שהקוד הקודם עדיין תקף השחרור מתבצע בהצלחה בעוד שלמעשה בעקבות הכישלון הראשון המכשיר ייצר קוד חדש שטרם השתמשו בו). התוצאה היא שהקוד השני יכול לשמש את הגנב מאוחר יותר. ההתקפה המתוארת אינה מכוונת נגד הצופן עצמו אלא רק על אופן השימוש בו.

ראו גם

• צופן בלוקים
• KATAN
• AES

הערות שוליים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

24338692KeeLoq