DES

DES
מידע כללי
תכנון	IBM ו-NSA
פרסום	1977
מבוסס על	צופן לוציפר
גרסאות מתקדמות	Triple DES, G-DES, DES-X, LOKI89, ICE
מבנה הצופן
אורך מפתח	56 סיביות
אורך בלוק	64 סיביות
מבנה	רשת פייסטל מאוזנת
מספר סבבים	16
קריפטואנליזה
	ההתקפות הטובות ביותר המוכרות כיום נגד DES הן קריפטואנליזה ליניארית וקריפטואנליזה דיפרנציאלית והן אינן מעשיות. בשל המפתח הקצר, הצופן ניתן לפיצוח על ידי כוח גס בעזרת חומרה ייעודית, ושיטות אחרות החליפו אותו בהדרגה.

תקן הצפנת מידע (באנגלית: Data Encryption Standard; בראשי תיבות: DES) הוא צופן בלוקים שפותח ב-1974 במרכז המחקר של IBM "תומאס ג'יי ווטסון", יורקטאון הייטס שבמחוז וסטצ'סטר בניו יורק, בשיתוף פעולה עם הסוכנות לביטחון לאומי של ממשלת ארצות הברית. האלגוריתם התקבל בשנת 1976 על ידי לשכת התקנים הלאומית של ארצות הברית (ששמה שונה מאוחר יותר ל-NIST) כחלק מדרישת תקן עבור הממשל האמריקאי להצפנת נתונים למטרות אזרחיות, ושימש כתקן למטרה זו עד נובמבר 2001, אז הוחלף בתקן החדש Advanced Encryption Standard. למרות זאת DES נמצא עדיין בשימוש בגרסה המשולשת שלו, בעיקר בתחום הבנקאות.

מבנה הצופן

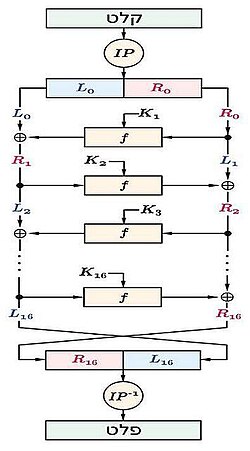
DES הוא צופן בלוקים סימטרי איטרטיבי שיועד בעיקר לחומרה. הוא מקבל בלוק טקסט קריא שהוא מחרוזת של 64 סיביות (8 בתים) ומפיק בלוק מוצפן באורך זהה. הפונקציה הפנימית של הצופן מתבצעת בשש עשרה חזרות בעזרת מפתח סודי באורך 64 סיביות (שמתוכן רק 56 סיביות בשימוש). צופן DES היה לצופן הראשון בקנה מידה גדול שהתבסס על רשת החלפה-תמורה לפי הפרדיגמה של קלוד שאנון, שהיא שילוב של הפעולות החלפה, תמורה וחיבור עם מפתח סודי במבנה הנקרא רשת פייסטל. זהו מבנה קריפטוגרפי הקרוי על שמו של הורסט פייסטל, יושם לראשונה בצופן לוציפר וידוע כמבנה בטוח. יתרונו הוא שהוא הופך כל פונקציה לא בהכרח הפיכה, לפרמוטציה. הפונקציה הפנימית של הצופן נחשבת לאינוולוציה, במובן שאם מפעילים את אותה הפונקציה פעמיים בזה אחר זה על אותו קלט מתקבל הקלט המקורי. לכן אפשר להשתמש בפונקציה אחת הן להצפנה והן לפענוח מה שחוסך בשערים לוגיים ומקטין את נפח החומרה. באופן כללי, מחלקים את בלוק הקלט לשני חצאים, ימין ושמאל בהתאמה ובכל סבב מצפינים את החצי השמאלי עם תוצאת הפונקציה שמופעלת על החצי הימני יחד עם מפתח הסודי נפרד, שני החצאים מחליפים מקומות וחוזרים שוב על אותה פעולה. בכל סבב רק החצי השמאלי משתנה ואילו החצי הימני נותר ללא שינוי, כשהוא הופך לחצי השמאלי בסבב הבא וחוזר חלילה. בפענוח מפעילים את אותה הפונקציה אך משתמשים במפתח בסדר הפוך.

תיאור הצופן

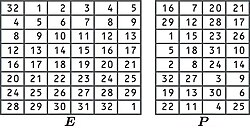
הקלט הוא בלוק טקסט קריא בגודל 64 סיביות ומפתח הצפנה סודי $\ K$ בגודל 64 (בפועל 56) סיביות. באמצעות תהליך הכנת המפתח המתואר להלן, מרחיבים את המפתח ומחלקים אותו ל-16 מקטעים בני 48 סיביות כל אחד. כאשר כל מקטע משמש עבור סבב בודד. מכינים 8 תיבות החלפה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ S_1,S_2,...,S_8} הנקראות בקיצור S-box. הן מייצגות אוסף של פונקציות לא-ליניאריות שמקבלות קלט באורך 6 סיביות ומחזירות פלט באורך 4 סיביות בהתאם לטבלת הערכים הקבועה המוצגת להלן.

מכינים "תיבת הרחבה" (הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ E} בתרשים) ו"תיבת תמורה" (הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ P} בתרשים), המייצגות פונקציות מיפוי לפי ערכים קבועים. התיבה E (קיצור של Expansion) היא תיבת תמורה/הרחבה, שתפקידה להכין את הקלט להחלפה בתיבות ההחלפה. היא מרחיבה את הקלט מ-32 סיביות ל-48 סיביות. 16 מתוך 32 סיביות הקלט מועתקות פעמיים למקומות שונים כמתואר בתרשים. למשל הסיבית במיקום הרביעי בקלט מועתקת למיקומים החמישי והשביעי בפלט. מכינים תיבת תמורה קבועה הנקראת P-box (קיצור של Permutation) שמשנה את סדר הסיביות של הפלט בסוף כל סבב תוך שמירה על גודלו. כזכור, היות שהצופן מיועד למימוש בחומרה, העתקת סיביות היא מלאכה קלה, זה רק עניין של חיווט. בתחילת הצופן לפני הפעלת הפונקציה הפנימית הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} מבצעים תמורה חד פעמית על כל סיביות הקלט באמצעות תיבת תמורה סטטית הנקראת הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle IP} ובסיום כל 16 הסבבים מעבירים את הפלט בתיבת התמורה ההופכית לה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ IP^{-1}} (שתיהן מוצגות בתרשימים משמאל). לפעולה זו אין השפעה על ביטחון הצופן ומקובל להתעלם ממנה כשמנתחים אותו. הסיבה לתוספת זו כמו שיקולים אחרים שהנחו את מפתחי הצופן לא היו נהירים בעיקר בשל העובדה שהם נחשבו לסוד לאומי. לדברי דון קופרשמידט הסיבה לתוספת זו טכנית בלבד, בשל העובדה ש-DES פותח בחומרה והחיווט היה נוח בצורה זו. סדר הפעולות בכל הסבבים זהה. תחילה מחלקים את קלט האלגוריתם לשני חצאים הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ L_0, R_0} בהתאמה ובכל סבב מבצעים כדלהלן:

L_{i}=R_{i-1}

,

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_i = L_{i-1} \oplus f(R_{i-1}, K_i)}

כאשר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ f(R_{i-1},K_i)=P(S(E(R_{i-1}) \oplus K_i))} .

במבנה זה פעולת הפונקציה הפנימית הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} מתבצעת רק על מחצית הקלט (היינו 32 סיביות). כאשר המחצית הימנית משמשת כקלט לפונקציה והפלט שלה משמש להצפנת המחצית השמאלית בחיבור XOR. שימו לב שהמחצית הימנית הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{i-1}} אינה מוצפנת אלא מועתקת כמו שהיא למחצית השמאלית של הסבב הבא. תפקידה הוא לשמש כמו מפתח הצפנה להצפנת המחצית השמאלית בכל סבב ולכן היא צריכה להישאר ללא שינוי כדי לאפשר פענוח לאחר מכן. הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} מורכבת מרשת החלפה-תמורה שהיא שילוב של שלוש פונקציות: הפונקציה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle E} שממפה "ומגדילה" את הקלט לפלט של 48 סיביות יחד עם תיבות ההחלפה ותפקידן הוא לבצע פעולה אי-ליניארית על הקלט, התמורה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle P} שתפקידה לפזר את הפלט והפונקציה השלישית שמחברת את הפלט עם חלק מהמפתח הסודי.

פירוט מהלכי הצופן

קלט: טקסט קריא

M

המיוצג כמחרוזת 64 סיביות על ידי המערך הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle m_1,m_2,...,m_{64}} . מפתח הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle K} שהוא מחרוזת של 64 סיביות המיוצגת על ידי הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_1,k_2,...,k_{64}} .

פלט: מחרוזת הסיביות הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle C=c_1,c_2,...c_{64}} .

1. הכנת מפתח

את המפתח הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle K} מרחיבים למערך של 16 כניסות בגודל 48 סיביות (סך הכול 768 סיביות) כדלהלן:

מכינים מערך עזר $v$ באורך 16 כניסות שערכיו לפי האינדקס הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle i} הם; עבור הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle i\in\{1,2,9,16\}} מציבים הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_i=1} בכל היתר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_i=2} .
משתמשים בטבלה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{PC1}} כדי להעתיק את סיביות המפתח $K$ לשני משתנים מקומיים הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle C,D} בגודל 28 סיביות כל אחד בהתאמה לפי הסדר המופיע בטבלה. כלומר הערך ההתחלתי יהיה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_0=k_{57},k_{49},k_{41},...,k_{36}} ו-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle D_0=k_{63},k_{55},...,k_4} . יש לשים לב שלא כל הסיביות הועתקו (רק 56 מתוך 64). ההעתקה מתבצעת ברמת סיביות לפי האינדקס, כלומר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_{57}} פירושו העתקת הסיבית ה-58 מהמפתח הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle K} למקום הראשון במשתנה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_0} (הספירה מתחילה מאפס).
הכנת 16 תת-מפתחות. עבור $i=1$ $i=1$ עד הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 16} מבצעים:
1. הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle C_i=(C_{i-1} \lll v_i)} , כלומר תוצאת הערך הקודם של הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle C} לאחר הזזה מעגלית לשמאל לפי הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_i} .
2. הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle D_i=(D_{i-1} \lll v_i)} , באופן דומה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle D} הוא תוצאת הזזה מעגלית לשמאל של ערכו הנוכחי $v_{i}$ פוזיציות.
3. הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle K_i=\text{PC2}(C_i \ \| \ D_i)} . משרשרים ביחד את שני החלקים למערך בגודל 56 סיביות הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle b_1,b_2,...,b_{56}} ונעזרים בטבלה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{PC2}} כדי לבחור 48 סיביות מתוכן עבור מפתח הסבב הנוכחי, לפי האינדקסים (כלומר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle K_i=b_{14},b_{17},...,b_{32}} ).

2. תמורה פותחת

משתמשים בטבלה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{IP}} כדי לערבב את סדר סיביות המסר; הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{IP}(m_1,m_2,...,m_{64})} ומחלקים את התוצאה לשני חצאים הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_0,R_0} . ערכי המחצית השמאלית הם הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_0=\{m_{58},m_{50},...,m_8\}} וערכי המחצית הימנית הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_0=\{m_{57},m_{49},...,m_7\}} . פעולה זו אינה קריפטוגרפית.

3. הסבבים

עבור הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle i=1} עד הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 16} מבצעים לפי הנוסחה המתוארת לעיל, תחילה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_i=R_{i-1}} ומחשבים את הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(S(E(R_{i-1})\oplus K_i))} כדלהלן:

הרחבה. מעתיקים את הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{i-1}=\{r_1,r_2,...,r_{32}\}} ממערך של 32 סיביות למערך הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle T} באורך 48 סיביות לפי הטבלה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{E}} . לאחר ההרחבה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle T=\{r_{32},r_1,r_2,...,r_{32},r_1\}} (שימו לב שסיביות מסוימות מועתקות יותר מפעם אחת).
מפתח. מבצעים XOR עם המפתח המורחב המתאים לסבב הנוכחי: הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle T = T\oplus K_i} .

קובץ:S-box indexing.png

החלפה. מחלקים את המערך הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle T} לשמונה כניסות הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle (B_1,B_2,...,B_8)} כל אחת מהן באורך 6 סיביות המסומנות הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \{b_1,b_2,...,b_6\}} ומבצעים החלפה של כל הכניסות עם שמונה תיבות ההחלפה המתאימות; הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_1(B_1),S_2(B_2),...,S_8(B_8)} . כל תיבת החלפה ממפה מחרוזת של שש סיביות קלט למחרוזת של ארבע סיביות המצויות בשורה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle r} בעמודה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle c} בטבלה. כאשר מספר השורה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle r=2\cdot b_1+b_6} הוא מספר שלם באורך שתי סיביות בטווח הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle [0..3]} . ארבע הסיביות הנותרות הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle b_2b_3b_4b_5} מייצגות מספר שלם בבסיס 2 בטווח הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle [0..15]} (ספרה הקסדצימלית אחת) שמשמש כמספר העמודה. לדוגמה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle S_1(\text{''011011''})} מניב הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle r=1} ו-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle c=13} והפלט הוא הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 5} .
תמורה. משתמשים בתיבת התמורה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{P}} כדי לסדר מחדש את סיביות הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle T} לפי האינדקסים. כלומר התוצאה תהיה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle T=\{t_{16},t_{7},...,t_{25}\}} .
מצפינים את החלק השמאלי: הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_i=L_{i-1}\oplus T} .

4. סיום

שני החצאים האחרונים הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{16},L_{16}} מתחלפים ביניהם.
מבצעים את התמורה המסיימת ההופכית הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{IP}^{-1}} , כלומר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle C=\{b_{40},b_8,...,b_{25}\}} . שוב פעולה זו אינה קריפטוגרפית.
התוצאה היא הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle C} .

וקטור בדיקה

המסר הוא הטקסט " Now is the time for all" באורך 24 אותיות (בקידוד ASCII) ומפתח ההצפנה הוא המחרוזת בייצוג הקסדצימלי:

Key = 0123456789ABCDEF

התוצאה היא הטקסטים הבאים בבסיס הקסדצימלי:

N o w i s t h e t i m e f o r a l l Plaintext = 4E6F772069732074 68652074696D6520 666F7220616C6C20 Ciphertext = 3FA40E8A984D4815 6A271787AB8883F9 893D51EC4B563B53

פענוח

הפענוח מתבצע עם אותה פונקציה ועם אותו מפתח אך בסדר הפוך. כלומר בתהליך הרחבת המפתח לעיל מתחילים מהמפתח הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle K_{16}} ויורדים עד הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle K_{1}} . הפעולות ${\text{IP}}$ מתחילת ההצפנה ו-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{IP}^{-1}} מסופה למעשה מבטלות אחת את השנייה כי הן פעולות הופכיות, לכן אפשר להתעלם מהן. מה שמותיר אותנו עם שני החצאים האחרונים הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{16},L_{16}} מהסבב האחרון של ההצפנה. כעת, מייד עם תחילת הלולאה הראשית בפענוח הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle L_{16}=R_{15}} (כזכור במעבר מסבב לסבב החצי הימני אינו משתנה אלא רק מחליף מקום עם החצי השמאלי) לכן הפעולה הבאה:

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{16}\oplus f(L_{16},K_{16})}

היא למעשה אינוולוציה והיא שקולה ל:

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle (L_{15}\oplus f(R_{15},K_{16}))\oplus f(R_{15},K_{16})=L_{15}}

החלק השמאלי ביותר המצוי בסוגריים הוא בדיוק הפעולה מהסבב האחרון של ההצפנה ואילו הפעולה הבאה אחריה היא מהסבב הראשון של הפענוח. אפשר לראות ששתי הפעולות מבטלות אחת את השנייה. על כן לאחר הסבב הראשון למעשה חוזרים צעד אחד לאחור ומתקבלים החצאים הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_{15},L_{15}} (מהסבב הקודם של ההצפנה). בסבב הבא מבצעים את אותה פעולה עם הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle K_{15}} וכן הלאה ובדרך זו משחזרים את יתר הסבבים.

תהליך הכנת המפתח

לצופן DES דרושים 16 תת-מפתחות, כל אחד מהם באורך 48 סיביות ומתאים לסבב בודד (סך הכול 768 סיביות). להכנת המפתחות DES משתמש בשתי טבלאות סטטיות הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle PC1} ו-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle PC2} (המוצגות בטבלאות הבאות). איתם מרחיבים את המפתח הסודי שמסופק על ידי המשתמש ל-16 תת-מפתחות. מתעלמים מהסיביות הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_8,k_{16},...,k_{64}} (כל סיבית שמינית) הנחשבות לסיביות זוגיות. באמצעות הטבלה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle PC1} מחלקים את 56 הסיביות האפקטיביות לשני משתנים הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle C} ו-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle D} בני 28 סיביות כל אחד. מבצעים הזזה מעגלית לשמאל של סיביות המשתנים הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle C} ו-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle D} בסיבית אחת או שתיים (בהתאם לערך התלוי במיקום הסיביות, עבור סבבים 1, 2, 9, 16 מזיזים ב-1 עבור היתר מזיזים ב-2) משתמשים בטבלה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle PC2} כדי לאחד את סיביות המשתנים לבלוק מפתח בגודל 48 סיביות. וחוזרים על פעולה זו 16 פעמים עבור כל 16 הסבבים של הצופן.

PC-1 (שמאל)
9	17	25	33	41	49	57
18	26	34	42	50	58	1
27	35	43	51	59	2	10
36	44	52	60	3	11	19

‎

PC-1 (ימין)
15	23	31	39	47	55	63
22	30	38	46	54	62	7
29	37	45	53	61	6	14
4	12	20	28	5	13	21

‎

PC-2
28	3	5	1	24	11	17	14
4	12	19	23	10	21	6	15
2	13	20	27	7	16	8	26
40	30	55	47	37	31	52	41
56	39	49	44	48	33	45	51
32	29	36	50	42	46	53	34

מפתחות חלשים וחלשים למחצה

על מנת שהצופן יצליח להסתיר היטב את הטקסט המקורי, תהליך הכנת המפתח מנסה לשוות למפתח המורחב מראה אקראי ככל האפשר. כבר ב-1973 התגלה שמפתחות הצפנה מסוימים עלולים לייצר מפתח מורחב בעל תבנית לא אקראית ניכרת שהתוצאה שלה בלתי צפויה. למשל אם המשתנה הפנימי C מכיל 28 אפסים והמשתנה D מכיל 28 אחדים ייווצר מצב שהצפנת DES תהיה זהה לפענוח DES עם אותו מפתח. כלומר:

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{DES}_K(M)=\text{DES}_K^{-1}(M)}

לכן אם מצפינים טקסט כלשהו עם אחד מהמפתחות החלשים פעמיים מתקבל הטקסט המקורי. ישנם ארבעה מפתחות החלשים ב-DES:

0x0101010101010101
0xFEFEFEFEFEFEFEFE
0xE0E0E0E0F1F1F1F1
0x1F1F1F1F0E0E0E0E

כזכור, כל סיבית מפתח שמינית נקראת סיבית זוגיות ולמעשה הן אינן משתתפות כלל בהצפנה. אם סיבית הזוגיות אינה נבדקת גם מפתח שכולו אפסים או אחדים יתנהג באותו אופן.

מפתחות הצפנה "חלשים למחצה" הם מפתחות שגורמים למצב שבו המפתח המורחב המתקבל מוגבל לשני תת-מפתחות בלבד כשהם חוזרים על עצמם בזוגות, ולהם התכונה הבאה:

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle E_{K_1}(E_{K_2}(M))=M}

כלומר הצפנה עם מפתח אחד ואז הצפנה של התוצאה עם המפתח השני מחזירה את המקור. קיימים שישה זוגות של מפתחות DES חלשים למחצה והם:

0x011F011F010E010E, 0x1F011F010E010E01
0x01E001E001F101F1, 0xE001E001F101F101
0x01FE01FE01FE01FE, 0xFE01FE01FE01FE01
0x1FE01FE00EF10EF1, 0xE01FE01FF10EF10E
0x1FFE1FFE0EFE0EFE, 0xFE1FFE1FFE0EFE0E
0xE0FEE0FEF1FEF1FE, 0xFEE0FEE0FEF1FEF1

תיבת ההחלפה S-box

קובץ:DES S-boxs.png

תיבות ההחלפה של DES

תיבת ההחלפה הנקראת S-box (קיצור של Substitution box ראה תרשים) מייצגת פונקציות החלפה אי-ליניאריות קבועות המחזירות ערכים מהטבלה על פי אינדקס שהוא פונקציה של הקלט. תיבות ההחלפה של DES הן מקור חוסנו, הפונקציות שהן מייצגות הן הפעולות האי-ליניאריות היחידות המופעלות על הקלט ואלמלא הן הצופן היה ניתן לפריצה בקלות. בדיעבד מסתבר כי התיבות עוצבו באופן כזה שהצופן יהיה עמיד יחסית כנגד קריפטואנליזה דיפרנציאלית. עוד ידוע כי גם ה-NSA היה מעורב בתכנון תיבת ההחלפה של DES ואף שינה אחדים מן הערכים מנימוק לא ידוע, ההערכה המקובלת כיום היא שהשינויים נועדו לחזק את הצופן כנגד ההתקפה הדיפרנציאלית שהייתה ידועה להם ולמפתחי הצופן ב-IBM כבר אז.

מצבי הפעלה

DES הוא דטרמיניסטי לכן הצפנה חוזרת של בלוקים זהים עם מפתח זהה תניב בלוק מוצפן זהה. עובדה זו עלולה להוות פתח להתקפה כנגד הצופן כי ניתן להיעזר בבלוקים זהים כדי לבצע ניתוח סטטיסטי של הצופן ולחלץ בדרך זו מידע מסוים אודות טקסט המקור. הפתרון לכך הוא יישום האלגוריתם באחד ממצבי ההפעלה המבטלים את יתירות הצופן. במצב ההפעלה משרשרים בלוקי צופן באופן שכל בלוק של טקסט המקור עובר תחילה XOR עם תוצאת ההצפנה של הבלוק הקודם. כך ששני בלוקים של טקסט מקור זהים יובילו לפלט צופן שונה. לצורך הבלוק הראשון משתמשים במפתח נוסף המכונה וקטור אתחול (Initialization Vector) או IV שגודלו כגודל הבלוק, אותו מחברים ב-XOR עם בלוק המידע הראשון.

ביטחון

הקריפטואנליזה הבולטת ביותר והראשונה נגד DES שסיבוכיותה טובה מעט יותר מכח גס, התגלתה על ידי אלי ביהם, כיום פרופסור בטכניון והמנחה שלו לדוקטורט עדי שמיר, כיום פרופסור במכון ויצמן למדע. הם פרסמו ב-1990 את עבודת הדוקטורט שלו שעסקה בקריפטואנליזה דיפרנציאלית – טכניקה רבת עוצמה שהתגלתה ככלי יעיל נגד אלגוריתמים סימטריים מודרניים רבים. אך קריפטואנליזה דיפרנציאלית מסוגלת לגלות מפתח הצפנה של DES עם הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2^{47}} דגימות קלט-פלט נבחרות של האלגוריתם לפי מודל התקפת גלוי-נבחר שזה אינו מעשי. ההתקפה טובה יותר המוכרת כיום נגד DES נקראת קריפטואנליזה ליניארית שמציעה שיפור על פני קודמתה. מלבד יכולתה לגלות מפתח DES עם הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2^{43}} קלטים, אין צורך עבורה בטקסט-מקור נבחר אלא כל טקסט אפשרי. התקפה זו נקראת התקפת גלוי-ידוע. התקפה אחרת מודרנית יותר היא התקפה אלגברית של ניקולס קורטויס וגרגורי בראד משנת 2007^[1], שהיא תחום מתפתח בקריפטואנליזה מודרנית. זוהי התקפה קריפטוגרפית הפועלת רק עם טקסט מקור יחיד והיא מנצלת אלגוריתמים לפתרון בעיות SAT כדי לגלות חולשות אלגבריות בצופן. DES נופל בקטגוריה של צפנים סימטריים הנקראת HFE שמבוססת על הקושי שבפתרון משוואות ריבועיות מרובות נעלמים שידועה כבעיית NP-קשה. אמנם מבחינה מעשית כאשר מערכת המשוואות "דלילה" אפשר לפעמים לפתור בעיה זו ביעילות, אך בפועל התקפה זו מצליחה רק נגד ששה סבבים של הצופן אבל היא אינה מעשית נגד DES במלואו.

ההתקפה הדיפרנציאלית והליניארית דורשות כמות עצומה של טקסטים מוצפנים ומקורותיהם (בסדר גודל של מאות טרה-בייט) על מנת למצוא את מפתח ההצפנה ולכן אינן מהוות איום ממשי על האלגוריתם. עובדה זו מעידה על חוסנו ועל טיבו של האלגוריתם יותר מאשר על חולשתו. למרות כל השנים טרם נמצאה התקפה היעילה באופן משמעותי מכח גס. מסתבר שההתקפה המעשית היחידה נגד DES היא התקפת כוח גס מקבילית באמצעות חומרה ייעודית. ב-1993 טען מיכאל ויינר שאפשר לבנות בהשקעה של כמיליון דולר מכונה שתפצח את DES בתוך 3.5 שעות במקרה הממוצע. לפי התכנון המקורי שלו המכונה צריכה להכיל כ-57,000 שבבים המסוגלים להריץ את DES במקביל. מאוחר יותר נבנתה מכונה כזו הלכה למעשה ובעלות נמוכה בהרבה. הארגון Electronic Frontier Foundation בנה מכונה לשבירת צופן DES בעלות של 250,000 דולר שבאמצעותה גילוי המפתח מתבצע בתוך יומיים וחצי בקירוב. כיום ניתן בהחלט לבנות מכונות מסוג דומה במחירים נמוכים בהרבה ובזמנים טובים יותר במידה ניכרת.

התקפה אחרת כנגד DES הנקראת התקפת יום הולדת היא התקפה אקראית מקבילית היעילה אף יותר מההתקפות המתוארות. התקפה זו מנצלת את תופעת פרדוקס יום ההולדת הידועה ומתבססת על ההנחה שהסיכויים ששני מפתחות שונים שנבחרו באקראי יניבו תוצאה זהה (עם טקסט מקור קבוע), גבוהים. Quisquater ו-Delescaille הראו שאפשר בהתקפה כזו לגלות מפתח DES ב-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ 2^{55}} ניסיונות במקרה הממוצע.

גרסאות מתקדמות

חולשתו העיקרית של DES היא גודל מפתח ההצפנה. גודל המפתח האפקטיבי של DES הוא רק 56 סיביות, שמונה מתוך 64 סיביות המפתח נחשבות כסיביות זוגיות ואינן משפיעות על ההצפנה. בעיקר בשל עובדה זו נחשב DES בימינו כ"הצפנה חלשה" ואינו בטוח לשימוש בגרסה הבסיסית. דרך בטוחה יותר וזולה ליישום DES היא הצפנה מרובה. כלומר הצפנה חוזרת של הטקסט עם מפתחות הצפנה שונים. שיטה אחת כזו נקראת "2DES" או DES כפול. אם הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ K_1,K_2} הם שני מפתחות DES שונים בגודל 56 סיביות כל אחד, ו-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ M} הוא המסר המיועד להצפנה, השיטה היא:

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \mbox{DES}2=\mbox{DES}_{K_2}(\ \mbox{DES}_{K_1}(\ M\ ))}

במקרה זה מתקבל צופן DES עם מפתח הצפנה בגודל 112 סיביות. אף לא אחת מההתקפות המתוארות לעיל ישימה כנגד צופן עם מפתח בסדר גודל כזה. גם לא מתקפת כוח גס מקבילית על חומרה ייעודית. אולם מסתבר ששיטה זו פגיעה לתקיפת היפגשות באמצע. בהתקפה זו מנצלים זיכרון על חשבון זמן ביצוע, אם מאחסנים טבלת גיבוב של הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ 2^{56}} הצפנות DES עם מפתחות שונים הממוינות לפי סדר וחיפוש התנגשויות, אפשר לקצר את זמן ההתקפה ל-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ 2^{57}} . כמות הזיכרון האדירה הדרושה להתקפה כזו עושה אותה כמעט בלתי ישימה באופן מעשי, אך ישנן שיטות לצמצום עלויות הזיכרון כך שאפקטיבית סיבוכיות התקפת כוח גס נגד DES כפול אינו עולה על הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2^{57}} .

שיטה טובה יותר נקראת DES משולש. קיימות שתי גרסאות DES משולש בשיטה הראשונה מצפינים את המידע שלוש פעמים עם שלושה מפתחות שונים, מסמנים זאת בקיצור EEE. השיטה הרווחת יותר היא וריאציה של DES משולש עם שני מפתחות המסומנת EDE. דהיינו מצפינים, מפענחים ושוב מצפינים. השיטה נראית כך:

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \mbox{DES}3=\mbox{DES}_{K_2}(\ \mbox{DES}^{-1}_{K_1}(\ \mbox{DES}_{K_2}(\ M\ )))}

כאשר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \mbox{DES}^{-1}_{K_1}} נקרא פענוח עם המפתח הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ K_1} . הסיבה למבנה זה היא בעיקר לצורך תאימות לחומרה הקיימת. ההתקפות המתוארות לעיל אינן ישימות כנגד שיטה זו ולמרות היותה איטית יותר היא נמצאת בשימוש נרחב כיום. כאמור בשל טכניקת היפגשות באמצע, אפקטיבית ביטחון DES משולש הוא רק הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2^{112}} .

DES-X

גרסה אחרת של DES שפותחה על ידי רון ריבסט מחברת RSA נקראת DES-X. בשיטה זו מצפינים את המידע שלוש פעמים בתוספת שתי מחרוזות אקראיות בגודל 64 סיביות. דרך אחת לייצג זאת היא XEX (הצפנה בשילוב XOR לפניה ואחריה). אם הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ K_1} הוא מפתח ההצפנה ו-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ K_2, K_3} הם מחרוזות אקראיות באורך 64 סיביות השיטה היא:

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle C=K_3\oplus \text{DES-X}_{K_2}(M \oplus K_1)}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle M=K_1\oplus \text{DES-X}_{K_2}(C \oplus K_3)}

תיאור מילולי: בתהליך ההצפנה תחילה מחברים ב-XOR את הקלט עם המפתח הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle K_1} , את התוצאה מצפינים עם אלגוריתם DES כרגיל עם המפתח הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle K_2} ולאחר מכן מחברים את התוצאה האחרונה ב-XOR עם המפתח הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle K_3} . בפענוח מבצעים את הפעולות המתוארות בסדר הפוך.

ריבסט כינה את תוספת המפתחות הלבנה. הסימן הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \oplus} מייצג פעולת XOR. למרות היותה יעילה יותר מ-DES משולש, שיטה זו פחות נפוצה.

DESL ו-DESXL

DES נחשב לצופן מהיר בחומרה (כוונת המפתחים מלכתחילה הייתה לייעדו לחומרה) והוא מציג ביצועים טובים מאוד בחומרה אפילו בהשוואה לצפנים מודרניים. כאמור אם דרוש ביטחון גבוה יותר ממה שהצופן המקורי מציע, אפשר להשתמש בגרסת DES-X של ריבסט המתוארת לעיל עם שני מפתחות הצפנה סודיים נוספים. התקורה הנוספת הנובעת מהוספת שערי XOR של שני המפתחות הנוספים היא כ-14 אחוז. התוספת הזו מחזקת את הצופן נגד כוח גס והתקפת איזון זמן/זיכרון שהיא אפקטיבית נגד הגרסה המקורית. גם התקפות אחרות אינן ישימות נגד מבנה זה בשל תוספת המפתחות ולכן הוא נחשב בטוח מאוד, במיוחד לאור העובדה שזהו הצופן הוותיק והנחקר ביותר בהיסטוריה של ההצפנה. ידוע ש-DES מכיל תכונות אקראיות טובות והוא חזק באופן יוצא דופן נגד קריפטואנליזה דיפרנציאלית וליניארית. כאשר נדרש צופן קל משקל במיוחד, אפשר להתאים את DES-X על שימוש בתיבת החלפה אחת במקום בשמונה הקיימות ובכך מפחיתים באופן משמעותי את כמות השערים. לגרסה זו קוראים DESL (קיצור של DES Lightweight). היא הוצעה ב-2006 על ידי Gregor Leander, Christof Paar, Axel Poschmann, and Kai Schramm^[2]. ניתן לממשה בחומרה עם 1848 GE (תואמי שערים לוגיים), זאת מבלי לאבד מהתכונות הטובות של הצופן המקורי למעט החיסרון הברור של המפתח הקצר. אם משלבים את DES-X עם DESL (מוסיפים עוד שני מפתחות) מתקבל הצופן DESXL שהוא גם בטוח וגם מהיר מאוד במיוחד בחומרה מוגבלת משאבים וצריכת אנרגיה נמוכה כמו חיישנים לבישים או RFID. השינויים בצופן כמובן עלולים שלא במודע לפתוח פתח להתקפות קריפטוגרפיות חדשות, לכן הצופן אינו מומלץ כתחליף ל-AES אלא רק במקרים בהם מעדיפים להתפשר על ביטחון לצורך יעילות וקלות הטמעה במערכת מוגבלת. הרעיון הוא שבמקום לפתח צופן חדש אפשר לשנות מעט את הצופן הקיים ולקבל צופן טוב במחיר מועט.

ראו גם

AES

קישורים חיצוניים

מדיה וקבצים בנושא DES בוויקישיתוף

הספר Handbook of Applied Cryptography, פרק 7
Parallel Collision Search with Application to Hash Functions and Discrete Logarithms
DES, באתר אנציקלופדיה בריטניקה (באנגלית)

הערות שוליים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

30532169DES

[1] Algebraic Cryptanalysis of the Data Encryption Standard

[2] New Lightweight DES Variants

[1]

[2]

DES

תוכן עניינים