פאון ארכימדי
בגאומטריית המרחב, פאון ארכימדי הוא פאון קמור משוכלל למחצה, שאינו מנסרה או אנטי-מנסרה, ושלא כמו בפאונים האפלטוניים, לא כל פאותיו חופפות. בפרט, כל הפאות של פאון ארכימדי חופפות לאחד משני מצולעים משוכללים או יותר, אשר כולם בעלי אותו אורך צלע. כמו כן, כל הקודקודים זהים, כלומר, כל הפאות הנפגשות בקודקוד אחד חופפות לפאות הנפגשות בכל קודקוד אחר. את הפאונים הארכימדיים אפשר לבנות מן הפאונים האפלטוניים באמצעות בניות ויטהוף.
מקור השם
הפאונים הארכימדיים נקראים על שם ארכימדס, שעסק בהם בספר שכל עותקיו אבדו. בתקופת הרנסאנס, אמנים ומתמטיקאים העריכו "צורות טהורות", וגילו מחדש את הפאונים הללו. החיפוש הושלם בסביבות 1619, כאשר יוהאנס קפלר הגדיר את המנסרות, אנטי-מנסרות והגופים הבלתי-קמורים הידועים בשם פאוני קפלר-פוינסוט.
מיון
יש שלושה-עשר פאונים ארכימדיים, מהם שניים בעלי כיווניות ימנית או שמאלית, וביחד 15 פאונים שונים (עד כדי דמיון במרחב). פאון ארכימדי מאופיין על ידי תבנית הקודקודים, המכתיבה אלו מצולעים נפגשים בכל קודקוד. לדוגמה, בפאון שתבניתו 4.6.8 נפגשים בכל קודקוד ריבוע, משושה משוכלל, ומתומן משוכלל.
| שם (תבנית קודקודים) |
דמות שקופה | דמות אטומה | פריסה | פאות | מקצועות | קודקודים | טיפוס חבורת הסימטריה | |
|---|---|---|---|---|---|---|---|---|
| ארבעון קטום או טטרהדרון קטום (3.6.6) |
 (אנימציה) |

|

|
8 | 4 משולשים 4 משושים |
18 | 12 | Td |
| קובוקטהדרון (3.4.3.4) |
 (אנימציה) |

|

|
14 | 24 | 12 | Oh | |
| קובייה קטומה או הקסהדרון קטום (3.8.8) |
 (אנימציה) |

|

|
14 | 8 משולשים 6 מתומנים |
36 | 24 | Oh |
| תמניון קטום או אוקטהדרון קטום (4.6.6) |
 (אנימציה) |

|

|
14 | 6 ריבועים 8 משושים |
36 | 24 | Oh |
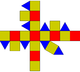
| רומביקובוקטהדרון
|
 (אנימציה) |

|
|
26 | 8 משולשים 18 ריבועים |
48 | 24 | Oh |
| קובוקטהדרון קטום או רומביקובוקטהדרון גדול (4.6.8) |
 (אנימציה) |

|

|
26 | 12 ריבועים 8 משושים |
72 | 48 | Oh |
| קובייה מסותתת או הקסהדרון מסותת |
 (אנימציה)  (אנימציה) |

|

|
38 | 32 משולשים 6 ריבועים |
60 | 24 | O |
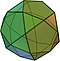
| איקוסידודקהדרון (3.5.3.5) |
 (אנימציה) |

|

|
32 | 20 משולשים 12 מחומשים |
60 | 30 | Ih |
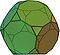
| דודקהדרון קטום (3.10.10) |
 (אנימציה) |

|

|
32 | 20 משולשים 12 מעושרים |
90 | 60 | Ih |
| איקוסהדרון קטום או כדור באקי
|
 (אנימציה) |

|
32 | 12 מחומשים 20 משושים |
90 | 60 | Ih | |
| רומביקוסידודקהדרון או רומביקוסידודקהדרון קטן (3.4.5.4) |
 (אנימציה) |

|

|
62 |
20 משולשים |
120 | 60 | Ih |
| איקוסידודקהדרון קטום או רומביקוסידודקהדרון גדול (4.6.10) |
 (אנימציה) |

|

|
62 | 30 ריבועים 20 משושים |
180 | 120 | Ih |
| דודקהדרון מסותת או איקוסידודקהדרון מסותת (2 צורות כיווניות) (3.3.3.3.5) |
 (אנימציה)  (אנימציה) |

|

|
92 | 80 משולשים 12 מחומשים |
150 | 60 | I |
הקוביה המסותתת והדודקהדרון המסותת הם כיווניים, משום שיש להם גרסה ימנית (בלטינית - levomorph) וגרסה שמאלית (dectromorph). צורות אלה הן תמונות מראה זו של זו. זוגות בעלי תכונה זו נקראים (למשל בכימיה) אננטימורפיים.
הפאונים הדואליים לפאונים הארכימדיים נקראים פאוני קטלן. יחד עם הדו-פירמידות והטרפזוהדרונים, אלו הם הפאונים שכל הפאות שלהם חופפות (גם אם אינן משוכללות).
מקורות
- Robert Williams, The Geometrical Foundation of Natural Structure: A Source Book of Design, 1979
ראו גם
קישורים חיצוניים
- פאון ארכימדי, באתר MathWorld (באנגלית) המזהה לא מולא ולא נמצא בוויקינתונים, נא למלא את הפרמטר.
| מצולעים ופאונים | ||
|---|---|---|
| מושגים | מצולע • פאון • קודקוד • צלע • מקצוע • פאה • זווית חיצונית • אלכסון | |
| מצולעים | ||
| לפי מספר צלעות | משולש • מרובע • מחומש • משושה • משובע • מתומן | |
| משולשים | משולש ישר-זווית • משולש שווה-שוקיים • משולש שווה-צלעות | |
| מרובעים | מקבילית • טרפז • טרפז שווה-שוקיים • מרובע ציקלי • דלתון • דלתון ריצוף • מעוין • מלבן • ריבוע | |
| כוכבים | פנטגרם • מגן דוד • אניאגרם | |
| תכונות | מצולע משוכלל • מצולע שווה-צלעות • מצולע קמור • כוכב | |
| פאונים | ||
| פאונים משוכללים | ארבעון • קובייה • תמניון • תריסרון • עשרימון | |
| פאונים ארכימדיים | ארבעון קטום • קובוקטהדרון • קובייה קטומה • תמניון קטום • רומביקובוקטהדרון • קובוקטהדרון קטום • קובייה מסותתת • איקוסידודקהדרון • דודקהדרון קטום • איקוסהדרון קטום • רומביקוסידודקהדרון • איקוסידודקהדרון קטום • דודקהדרון מסותת | |
| פאונים אחרים | פירמידה • מנסרה • אנטי-מנסרה • מקבילון • מעוינון • תיבה • איקוסיטטרהדרון | |
| תכונות | פאון משוכלל • פאון משוכלל למחצה • פאון ארכימדי | |
| הכללות | ||
| הכללות | סימפלקס • היפרקובייה • טסרקט | |
פאון ארכימדי23770936Q213486


