סינגולריות (מתמטיקה)
במתמטיקה, נקודה סינגולרית היא נקודה שבה פונקציה (בדרך כלל פונקציה מרוכבת) או משוואה דיפרנציאלית איננה מוגדרת היטב.
באנליזה מרוכבת
נקודת סינגולריות של פונקציה מרוכבת היא נקודה שבה הפונקציה אינה הולומורפית, אך כך שהיא הולומורפית בסביבתה. יש שלושה סוגים שונים של נקודות סינגולריות מבודדות, השונים זה מזה באופיים, וניתנים לאפיון באמצעות פיתוח הפונקציה לטור לורן סביב הסינגולריות.
סינגולריות סליקה
נקודת סינגולריות סליקה היא נקודה אשר הפונקציה שואפת בה לגבול סופי. מקור שמה של סינגולריות זו בכך שהשלמת הפונקציה באופן רציף בנקודה זו תיתן פונקציה אנליטית, כלומר, ניתן "לסלק" את הסינגולריות. טור לורן של פונקציה סביב נקודות סינגולריות סליקה מתאפיין בכך שלא מופיעים בו איברים עם חזקות שליליות - כלומר, טור לורן הופך לטור טיילור. כדוגמה לנקודת סינגולריות סליקה, ניתן להתבונן בנקודה עבור הפונקציה . ניתן "לסלק" את הסינגולריות של הפונקציה הזאת על ידי החלפת פונקציה זאת בפונקציה הרציפה:
הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle y_1\left(z\right)=\left\{ \begin{array}{ll} \displaystyle\frac{\sin z}{z}&z\ne0\\[4pt] 1&z=0 \end{array} \right. }
קוטב
קטבים מסדר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle n} הם נקודות סינגולריות בהן הפונקציה מתבדרת לאינסוף. טור לורן סביב נקודה כזו מתאפיין בכך שיש לו מספר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle n} סופי (הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ n\ge 1} ) של איברים עם חזקות שליליות. החזקה השלילית הגדולה ביותר בטור לורן של הפונקציה מכונה סדר הקוטב. אפשר לגרום לפונקציה להתכנס לערך סופי השונה מאפס על ידי הכפלה של הפונקציה ב-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(x-x_0\right)^n} . כדוגמה לקוטב בסדר גודל 3 של פונקציה מרוכבת, ניתן להתבונן בנקודה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle x=7} עבור הפונקציה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \displaystyle\frac{\sin x}{\left(x-7\right)^3}} . כאשר מכפילים את הפונקציה ב-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(x-7\right)^3} הפונקציה מתכנסת לערך סופי הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\sin7\right)} .
סינגולריות עיקרית
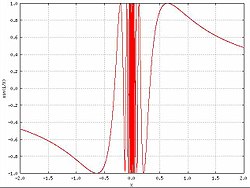
נקודות סינגולריות עיקריות הן אלה אשר לפונקציה אין גבול (סופי או אינסופי) בסביבתן. משפט קסורטי-ויירשטראס מאפיין נקודות אלה כנקודות אשר הפונקציה מקבלת ערכים הקרובים כרצוננו לכל נקודה מרוכבת בסביבתן. בניסוח אחר: תמונתה של כל סביבה של נקודת סינגולריות עיקרית היא צפופה במישור המרוכב. טורי לורן של פונקציה סביב נקודת סינגולריות עיקרית מכילים מספר אינסופי של איברים עם חזקות שליליות.
כדוגמה לפונקציה בעלת נקודת סינגולריות עיקרית ניתן לראות את הפונקציה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \sin\left(\frac{1}{z}\right)} , כיוון שלפונקציה הממשית הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \sin\left(\frac{1}{x}\right)} אין גבול בסביבת 0 גם לפונקציה המרוכבת הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \sin\left(\frac{1}{z}\right)} אין גבול בסביבת 0.
במשוואות דיפרנציאליות
עבור משוואה דיפרנציאלית ליניארית מסדר כלשהו, אפשר להגדיר נקודות סינגולריות באמצעות הצגתה כמשוואת אוילר. נקודות סינגולריות קורות כאשר המקדם של הנגזרת הגבוהה ביותר מתאפס. סביב נקודות סינגולריות אפשר לנחש פתרון בצורה של טור אינסופי, שיטה זו נקראת שיטת פרוביניוס.
ביריעות אלגבריות
אם V יריעה אלגברית ו-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,P \in V} נקודה על היריעה, אז P נקראת סינגולרית אם החוג המקומי המתקבל על ידי לוקליזציה של חוג הקואורדינטות של V באידיאל הראשוני של אוסף הפונקציות המתאפסות בP אינו חוג מקומי רגולרי. יריעה ללא נקודות סינגולריות היא יריעה חלקה.
משטח אלגברי במרחב האפיני התלת-ממדי מוגדר על ידי משוואה פולינומית אחת. ידוע שמספר נקודות הסינגולריות של משטח כזה חסום, כפונקציה של מעלת הפולינום. מקובל לסמן את המספר המקסימלי של נקודות הסינגולריות על עקום מהצורה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(x,y,z)=0} , כאשר P פולינום ממעלה d, ב-. הערכים הידועים של הפונקציה הם הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \begin{matrix} d & | & 1 & 2 & 3 & 4 & 5 & 6 \\ \hline \mu(d) & | & 0 & 1 & 4 & 16 & 31 & 65 \end{matrix}} . לדוגמה, למשטח קומר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ (x^2+y^2+z^2-2)^2 = 5((1-z)^2-2x^2)((1+z)^2-2y^2)} יש 16 נקודות סינגולריות, וזהו המספר המקסימלי האפשרי בדרגה זו. כמו כן ידוע ש-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ 99 \leq \mu(7)\leq 104} ו-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle 168 \leq \mu(8)\leq 174} . עבור ערכים גדולים של המעלה d, ידוע ש-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \frac{4}{9} \lessapprox \frac{\mu(d)}{d^3} \lessapprox \frac{5}{12}} .
בסכמות
באופן יותר כללי, אם הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,(X,\mathcal{O}_X)} היא סכמה ואם הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,P \in X} , אז P נקראת סינגולרית אם החוג הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{O}_P} אינו חוג מקומי רגולרי.
בהעתקות ליניאריות
יהי T אופרטור ליניארי או מטריצה ריבועית. אם T הפיך אז T נקרא גם רגולרי או לא-סינגולרי. אם T לא הפיך אז T נקרא גם לא-רגולרי או סינגולרי.
קישורים חיצוניים
| מיזמי קרן ויקימדיה |
|---|
 ערך מילוני בוויקימילון: נקדה סינגולרית |
32666327סינגולריות (מתמטיקה)