משפט גרין

משפט גרין הוא משפט באנליזה מתמטית המגדיר קשר בין אינטגרל קווי של פונקציה על עקום סגור ופשוט לבין האינטגרל הכפול על השטח החסום על ידי העקום. משפט גרין הוא מקרה פרטי דו-ממדי של משפט סטוקס. הוא נקרא על שם המתמטיקאי האנגלי ג'ורג' גרין.

למשפט שימושים רבים במתמטיקה ובהנדסה. לדוגמה, הבסיס המתמטי לפעולת הפלנימטר, שהוא מכשיר המודד שטח של צורה מישורית כלשהי, הוא משפט גרין, או נוסחת הסקטור של לייבניץ כמקרה פרטי שלו. ממשפט גרין נובעת נוסחת השרוך.

המשפט: תהי $C$ מסילה פשוטה סגורה, מכוונת חיובית (נגד כיוון השעון) וגזירה למקוטעין החוסמת שטח ב-$\mathbb {R} ^{2}$, ונסמן ב-$D$ את השטח החסום על ידי המסילה $C$. אם $P(x,y)$ ,$Q(x,y)$ פונקציות בעלות נגזרות חלקיות רציפות עד סדר ראשון בסביבה המכילה את $D$, אזי:

$\oint _{C}(P\,\mathrm {d} x+Q\,\mathrm {d} y)=\iint _{D}\left({\frac {\partial Q}{\partial x}}-{\frac {\partial P}{\partial y}}\right)\,\mathrm {d} x\mathrm {d} y$.

כאשר הביטוי משמאל מגדיר אינטגרל קווי על עקום סגור (ולכן סימון העיגול על סימן האינטגרל) ומימין מבוטא האינטגרל הכפול עבור שטח התחום הסגור $D$.

סימון מקובל בפיזיקה

מקרה שימושי במיוחד הוא כאשר הפונקציות $P,Q$ הן רכיבים של שדה וקטורי: ${\vec {f}}({\vec {r}})=(P,Q)$. הסימון המקובל הוא $P=f_{x},Q=f_{y}$. במקרה זה המשפט מקשר בין האינטגרל המשטחי על שטף הרוטור של השדה הווקטורי, לבין האינטגרל המסילתי של השדה. אם נסמן ב-${\hat {n}}$ את הווקטור הניצב למשטח, וב-${\vec {dl}}$ את אלמנט המסילה המקיפה את המשטח, ניסוח המשפט יהיה

$\oint _{C}{\vec {f}}\cdot {\vec {dl}}=\iint _{D}\left({\vec {\nabla }}\times {\vec {f}}\right)\cdot {\hat {n}}$

בניסוח הזה, המשפט הוא כללי יותר. הוא תקף לא רק כאשר התחום $D$ מוכל במישור, אלא גם במקרה כללי שבו $D$ הוא יריעה חלקה דו-ממדית פשוטת קשר, והעקום $C$ הוא שפת היריעה (שצריכה להיות גזירה למקוטעין).

שימוש לדוגמה: שדה מגנטי מסביב לתיל נושא זרם

זרם חשמלי מיצר שדה מגנטי.

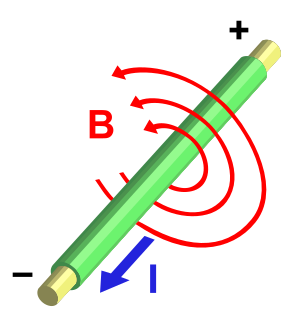
נניח כי נתון לנו תיל ישר, אינסופי, הנושא זרם $I$. הקשר בין הזרם לשדה המגנטי נתון (במקרה הסטטי) על ידי חוק אמפר:

${\vec {\nabla }}\times {\vec {B}}=\mu _{0}{\vec {J}}$

כאשר ${\vec {B}}$ הוא השדה המגנטי, ${\vec {J}}$ הוא צפיפות הזרם, ו-$\mu _{0}$ הוא קבוע הפרמיאביליות של הריק. נבנה משטח מעגלי מאונך לתיל ברדיוס $r$, שמרכזו נמצא על התיל (כמו קווי השדה האדומים בתמונה). נסמן את המשטח ב-$D$ ואת העקום שמקיף אותו ב-$C$. מכיוון שהמערכת סימטרית לסיבוב סביב התיל, השדה המגנטי לאורך $C$ קבוע. משיקולים אחרים ניתן לקבל שכיוון השדה המגנטי משיק ל-$C$ בכל נקודה. לכן, האינטגרל המסלולי על השדה המגנטי שווה פשוט ל:

$\oint _{C}{\vec {B}}\cdot {\vec {d}}l=\int _{C}B=2\pi rB$

כאשר $B=\left|{\vec {B}}\right|$. כעת נשתמש במשפט גרין ובחוק אמפר כדי לחשב את גודל השדה:

$2\pi rB=\oint _{C}{\vec {B}}\cdot {\vec {d}}l=\iint _{D}{\vec {\nabla }}\times {\vec {B}}\cdot {\hat {n}}=\iint _{D}\mu _{0}{\vec {J}}\cdot {\hat {n}}$

לפי הגדרה, האינטגרל על צפיפות הזרם הוא הזרם, ולכן קיבלנו $2\pi rB=\mu _{0}I$, או בניסוח המקובל יותר:

$B(r)={\frac {\mu _{0}I}{2\pi r}}$.

הוכחה עבור תחום מלבני

D הוא תחום החסום על ידי העקום הגזיר למקוטעין הבנוי מ: C₁, C₂, C₃, C₄

נוכיח כי מתקיים:

$\oint _{C}P\,dx=\iint _{D}\left(-{\frac {\partial P}{\partial y}}\right)\,dA\qquad \mathrm {(1)}$

עבור $D$ שהוא תחום פשוט מסוג 1 - תחום חסום על ידי שני ישרים מאונכים לציר x ושתי פונקציות גזירות של x (כמתואר בתמונה).

נגדיר:

$D=\{(x,y)|a\leq x\leq b,g_{1}(x)\leq y\leq g_{2}(x)\}$

כאשר $g_{1},g_{2}$ גזירות למקוטעין ב-$[a,b]$. נחשב את האינטגרל הכפול ב-(1):

$\iint _{D}\left(-{\frac {\partial P}{\partial y}}\right)\,dxdy=\int _{a}^{b}\!\!\int _{g_{1}(x)}^{g_{2}(x)}\left(-{\frac {\partial P}{\partial y}}(x,y)\right)\,dy\,dx=\int _{a}^{b}{\big \{}-P(x,g_{2}(x))+P(x,g_{1}(x))\,{\big \}}\,dx\qquad \mathrm {(2)}$

כעת נחשב את האינטגרל הקווי ב-(1): ניתן לרשום את $C$ כאיחוד ארבעת העקומים: $C_{4}$, $C_{3}$, $C_{2}$, $C_{1}$.

עבור $C_{1}$ נשתמש בהצגה הפרמטרית: $a<=x<=b$, $y=g_{1}(x)$, $x=x$

$\int _{C_{1}}P(x,y)\,dx=\int _{a}^{b}P(x,g_{1}(x))\,dx$

עבור $C_{3}$ נשתמש בהצגה הפרמטרית: $a<=x<=b$, $y=g_{2}(x)$, $x=x$ ולכן:

$\int _{C_{3}}P(x,y)\,dx=\int _{b}^{a}P(x,g_{2}(x))\,dx=-\int _{a}^{b}P(x,g_{2}(x))\,dx$

עבור $C_{2},C_{4}$, הערך של x זהה בשני גבולות האינטגרציה, ולכן

$\int _{C_{4}}P(x,y)\,dx=\int _{C_{2}}P(x,y)\,dx=0$

מסקנה:

$\oint _{C}P\,dx=\int _{C_{1}}P(x,y)\,dx+\int _{C_{2}}P(x,y)\,dx+\int _{C_{3}}P(x,y)\,dx+\int _{C_{4}}P(x,y)\,dx=\int _{a}^{b}P(x,g_{1}(x))\,dx-\int _{a}^{b}P(x,g_{2}(x))\,dx\qquad \mathrm {(3)}$

התוצאות במשוואות (3) ו-(2) זהות, ובכך קיבלנו את השוויון ב-(1).

באופן דומה ניתן להוכיח כי מתקיים:

$\oint _{C}Q\,dy=\iint _{D}\left({\frac {\partial Q}{\partial x}}\right)\,dA\qquad \mathrm {(4)}$

עבור $D$ שהוא תחום פשוט מסוג 2 - חסום על ידי שני ישרים מאונכים לציר y ושתי פונקציות גזירות של y.

משילוב (1) ו-(4) מתקבל כי עבור תחום מלבני (שהוא תחום פשוט מסוג 1 וגם תחום פשוט מסוג 2) מתקיים

$\oint _{C}(P\,dx+Q\,dy)=\iint _{D}\left({\frac {\partial Q}{\partial x}}-{\frac {\partial P}{\partial y}}\right)\,dA\qquad \mathrm {(5)}$

על ידי שימוש בתכונות של אינטגרלים (אדיטיביות על תחומים זרים, והיפוך סימן בהיפוך כיוון) ניתן לראות כי המשפט תקף עבור כל שטח שניתן לחלוקה למספר סופי של תחומים מלבניים.

ראו גם

• משפט גרין דיסקרטי

קישורים חיצוניים

מדיה וקבצים בנושא משפט גרין בוויקישיתוף

• משפט גרין, באתר MathWorld (באנגלית)
• פונקציות גרין, דף שער בספרייה הלאומית

הערות שוליים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

35678027משפט גרין