פיזור

פיזור גלי מים על ידי אי יבשתי

פיזור הוא שם כולל לתהליכים בפיזיקה בהם התנועה של גלים כגון אור, קול או חלקיקים נעים, מושפעת ממכשול או אי-אחידות מקומית בתווך דרכו הם עוברים. זהו כלי מרכזי לתיאור תופעות בתחומים שונים, כמו אופטיקה, מכניקת הקוונטים ופיזיקת חלקיקים. תופעה זו מוסברת באופן מתמטי על ידי תורת הפיזור תוך העזרות בגדלים פיזקליים כדוגמת חתך פעולה. דוגמאות להתנגשויות הגורמות לפיזור הן מגוונות וכוללות בין השאר קרינה קוסמית המפוזרת מהאטמוספירה, פיזור אלקטרונים על ידי גרעין אטום ואת שבירתם של גלי-ים במכשולים יבשתיים העומדים בדרכם. בשימוש המקובל, המונח כולל גם סטיה של קרינה מוחזרת מהזווית הנקבעת על ידי חוק ההחזרה.

היסטוריה

לורד ריילי

לאון ברילואן

מאחר שטבעם הגלי של חלקיקים התגלה רק במאה ה20, מושג הפיזור נתפס לראשונה בהקשר של גלי-אור נראה. ציון מוקדם של התופעה עוד במאה ה16 מוזכר על ידי לאונרדו דה וינצ'י בספרו "צבע האטמוספירה". בספר זה, מעלה דה וינצ'י השערה שהמקור לצבעם הכחול של השמיים הוא מפגשן של קרני אור מהשמש עם חלקיקים קטנים שעברו התאיידות.
השערה זו צפתה את תוצאות הניסוי שנערך על ידי הפיזיקאי האירי ג'ון טינדל כעבור 350 שנה, באמצע המאה ה-19. בניסוי זה, מצא טינדל שאור כחול מתפזר בעוצמה גבוהה יותר מאשר אור אדום כאשר עובר דרך תמיסה דלילה. בשנות ה-70 של המאה ה-19 ניסח לורד ריילי את המשוואות הקובעות את תלות אורך הגל בפיזור מחלקיקים קטנים. הודות לחוקים אותם ניסח ריילי, ההסבר לשאלת צבעם של השמיים ניתן לבסוף על ידי ג'יימס קלרק מקסוול שקבע שצבעם של השמיים הוא תוצאתו של פיזור קרניים אלקטרומגנטיות מהשמש על ידי מולקולות באטמוספירה.

במאה ה20, המשיכה ההתקדמות בחקר תופעת הפיזור; עבודתו של גוסטב מיי המתארת את פיזורם של גלים אלקטרומגנטיים על ידי מבנים ספיריים פורסמה ב-1908. פיזור מיי המתאר את פיזור האור מעצמים בעלי ממדים דומים לאורך הגל, קרוי על שמו. בשנת 1922, גילה הפיזיקאי הצרפתי לאון ברילואן שכאשר מאירים בקרינה מונוכרומטית דרך מדיום אופטי נוצרים פסים ("בנדים") בשולי מסלול ההארה המרכזי. ברילואן שיער שזוהי תוצאתו של היסט דופלר המתרחש בשל יצירתם של גלים אקוסטיים בעת מפגש הקרינה עם המולקולות.

בשנת 1924, העלה לואי דה ברויי את השערת הגל-חלקיק, תאוריה בעלת תרומה גדולה למכניקת הקוונטים, לפיה, ניתן להתייחס לחלקיק כגל. תאוריה זו איפשרה יישום תופעות גליות, הידועות מתחומים כמו אופטיקה ואקוסטיקה, על חלקיקי חומר. שימוש בפיזור חלקיקים היה הבסיס למספר פריצות דרך מדעיות, ביניהן, ניסוי רתרפורד והשימוש במיקרוסקופ אלקטרונים.
בשנת 1928 גילה ונקאטה רמאן את הפיזור האי-אלסטי, תופעה משמעותית בתיאורו הקוונטי של האור ובתחום הכימיה האנליטית. במקביל, גילו המדענים הרוסיים מנדלסון ולנדסנברג את אותה התופעה בניסויים שערכו עם קוורץ. גילויו של ראמאן הביא לריבוי פרסומים מדעיים עוקבים, מהבולטים שבהם מאמריו התאורטיים של ג'ורג' פלאצ'ק בשנות ה-30.

במחצית השנייה של המאה העשרים, עם התפתחות הלייזר והשיפור ביכולת לסנטז חלקיקים קטנים גברה ההתעניינות בפיזור על ידי חלקיקים קטנים. פיזור מסוג זה נמצא יישומי בתחומים דוגמת רפואה, ספקטרוסקופיה וארוסולים באטמוספירה. כמו כן, מחקר ניסויי באמצעות קרינת לייזר איפשר התקדמות במחקר ניסויי של אינטראקציית אור-חומר, פלזמונים וקוסמולוגיה.

מושגי יסוד

מרכזי פיזור

סוגי מכשולים או אי-אחידויות שהתנגשות עמם יכול לגרום לפיזור, נקראים לעיתים "מפזרים" או "מרכזי פיזור". בין מרכזי הפיזור ניתן למנות בין השאר: חלקיקים, בועות, טיפות, אדי מים, תנודות של צפיפות בנוזלים, פגמים במוצקים גבישיים, משטחים מחוספסים, תאים באורגניזמים וסיבי טקסטיל בבגדים. קרינה יכולה להתפזר ממרכז פיזור בודד, תופעה המכונה פיזור יחיד, או להתפזר מספר פעמים על ידי מספר מפזרים המקובצים יחד, תופעה המכונה פיזור מרובה. בעוד פיזור יחיד נתפס כתופעה אקראית, פיזור מרובה נתפס כדטרמיניסטי וניתן לניבוי באופן הסתברותי כמיצוע של מספר רב של אירועים אקראיים. תיאור זה של שתי התופעות לעיתים קרובות מקושר לדואליות גל-חלקיק.

פיזור יחיד

בפיזור יחיד, מיקומו המדויק של המפזר הבודד לרוב אינו ידוע ביחס למסלול הקרינה, על-פי עיקרון אי הוודאות. כתוצאה מכך, מסלולה של הקרינה המתפזרת לא ניתן לניבוי דטרמניסטי ונראה אקראי. תופעה זו ניתן להדגים על ידי תנועת אלקטרון בודד הנורה לעבר גרעין אטום. במקרה זה, מיקומו המדויק של גרעין האטום ביחס למסלול האלקטרון אינו ניתן למדידה, לכן, תנועת האלקטרון לאחר ההתנגשות אינה ניתנת לניבוי אלא רק כהתפלגות הסתברויות, כלומר, כתוצאה בעלת רוחב מסוים של שונות סטטיסטית. פתרון מסוג זה אופייני לבעיה ממכניקת הקוונטים. חשוב לציין, שקיימים מקרים פרטיים בהם פיזור יחיד ניתן לניבוי, כפי שקורה לעיתים כאשר קרן לייזר מפוזרת מחלקיק מיקרוסקופי, או בפיזור הנגרם על ידי מטרות מכ"ם מקרוסקופיות (כמו אדם או מטוס).

פיזור מרובה

בפיזור מרובה, מספר גבוה של אירועי פיזור אקראיים מביאים לתוצאה הנראית כדטרמיניסטית, ע"פ העיקרון הסטטיסטי לפיו אי-הוודאות (או השונות) קטנה ככל שדוגמים אוכלוסייה גדולה יותר. דוגמה לכך היא תנועתה של קרן אור דרך ערפל. במקרה זה, החלקיקים באוויר משמשים כמרכזי פיזור רבים. גם במקרה של פיזור מרובה קיימים יוצאים מהכלל; לעיתים יש חשיבות לפלוקטואציות אקראיות סביב הפתרון הדטרמיניסטי, בייחוד במקרים של קרינה קוהרנטית בהם פלוקטואציות אלו מכונות ספקלס (speckles). במקרים אחרים מספר אירועי הפיזור אינו גבוה מאוד, מה שמותיר רוחב אי-וודאות שאינו ניתן להזנחה ומקשה על יצירת מודל לניבוי המערכת.

פיזור אלסטי ואי אלסטי

כאשר לגל המתפזר אותה תדירות (או אנרגיה) של הגל לפני המפגש עם מרכז הפיזור, ההתנגשות מתוארת כפיזור אלסטי. כאשר הגל מאבד אנרגיה כתוצאה מההתנגשות (התנגשות פלסטית), או לחלופין, מקבל אנרגיה כך שתדירותו לאחר ההתנגשות גבוהה יותר ההתנגשות מתוארת כפיזור אי-אלסטי.

תורת הפיזור

תורת הפיזור היא מסגרת העבודה המתמטית והפיזיקאלית להבנת תופעת הפיזור של גלים או חלקיקים ומשמשת כלי מרכזי לתיאור תופעות באופטיקה, בתורת הקוונטים ובפיזיקת חלקיקים, כמו גם בתחומים נוספים. תאוריה זו היא למעשה פתרון של משוואות דיפרנציאליות חלקיות הפותרות את תנועתם של גופים העוברים אינטראקציה הדדית בתנאי גבול מוגדרים, למשל, תנועתו של חלקיק הפוגע במטרה ומשנה את כיוון תנועתו.
ניתן לסווג בעיה מסוג זה לשניים:
1) בעיית הפיזור הישיר - בה מנבאים את התפלגות הקרינה המפוזרת ע"פ תכונות מפזר ידועות.
2) בעיית הפיזור ההופכית - בה התפלגות הפיזור ידועה ומאפיינים את תכונות מרכז הפיזור.

בעיית הפיזור ההופכית נפוצה יותר בתחום הפיזיקה הניסויית, מאחר שלרוב, תכונות המפזר אינן ידועות והמידע הנתון, שזמינותו קלה יותר, הוא של התפלגות הקרינה המפוזרת. דוגמה לכך הוא פיזור בראג המאפשר את קביעתם של מבנים גבישיים בעזרת תבנית הפיזור של קרינת X.

ההיבט המתמטי לתיאור גלים הוא על ידי פתרון משוואת הגלים, כלומר, באמצעות השמתם של תנאי התחלה ותנאי גבול למשוואה דיפרנציאלית חלקית. הפונקציה הגלית יכולה לייצג את שינוייהם המחזוריים, בזמן או במרחב, של תכונות שונות, בהתאם לבעיה הפיזיקאלית אותה היא מתארת. לדוגמה: עבור אור, הפונקציה תייצג את גודל השדה האלקטרומגנטי; עבור קרן חלקיקים, הפונקציה תייצג את פונקציית הגל - ההסתברות להימצאות חלקיק במרחב; במקרה של גל אקוסטי או גל קול תייצג הפונקציה את שינויי הלחץ המתפשטים בחומר.

המקרה הפשוט ביותר להדגמה הוא העתקתם החד ממדית של חלקיקים ממסלול הקרן הבלתי מפוזרת לאחר פגיעתה במטרה כלשהי כאשר קצב הפיזור קבוע ופרופורציוני לשטף:
${dI \over dx}=-QI$
כאשר $x$ הוא העתק החלקיק ו-$I$ שטף הקרן.
זוהי למעשה משוואה דיפרנציאלית רגילה מסדר ראשון שהפתרון שלה הוא:
$I=I_{0}e^{-Q\triangle x}$
כאשר $I_{0}$ הוא השטף ההתחלתי של הקרן, $\triangle x=x-x_{0}$ ו-$Q$ הוא קבוע האינטראקציה שמשמעותו הפיזיקאלית משתנה בהתאם ליישום הבעיה. כפי שניתן לראות, פתרון זה מוביל למסקנה שהשטף דועך באופן מעריכי ככל שמתרחקים מהקרן הבלתי מתפזרת.
עבור פתרון של מקרים מורכבים יותר, כשהמטרה היא צבר של מרכזי פיזור רבים בעלי מיקום יחסי המשתנה באופן בלתי-צפוי, יש צורך לפתור סט משוואות עם משתנים שונים בהתאם ליישומה הפיזיקאלי של הבעיה.

חתך הפעולה לפיזור

חתך הפעולה של הפיזור הוא שטח המתאר את הסבירות של גל או חלקיק להתפזר על ידי מרכז פיזור, יחיד או מרובה. לגודל זה ממדים של שטח (מטר רבוע ביחידות SI) והוא משמש כפרמטר מתמטי והשוואתי יעיל. המקור ליחידת השטח נובע מיחס בין גדלים גאומטריים - שינוי הזווית המרחבית, לה יחידות של שטח, כתוצאה משינוי בשטח-החתך הדיפרנציאלי שהוא למעשה יחס דיפרנציאלי בין שטחים ומתאר את המיפתח הזוויתי של תנועת החלקיק בעקבות מפגשו עם המפזר. בנוסף, קיימת הקבלה בין הפרשנות הקלאסית של חתך הפיזור לפרשנותו הקוונטית, ובכך הוא מהווה גודל נוח לגישור בין שני תיאורים מרכזיים אלה .

הסבר גאומטרי

הפרשנות הקלאסית של חתך הפעולה לפיזור מסתמכת בעיקרה על שימוש בפרמטרים גאומטריים. וקטור ההתקדמות של החלקיק עובר דרך שתי נקודות: מרכזו ההתחלתי של החלקיק (נק' A) ומרכזו של המפזר (כדור אדום בשרטוט). ע"פ מודל זה, החלקיק או הגל מתוארים בכל זמן על ידי פרמטר ההשפעה (b) - גודלו של הרדיוס בשטח החתך המעגלי של החלקיק שמרכזו נמצא על וקטור ההתקדמות. כעת, נגדיר קטע העובר בין פרמטר ההשפעה, בזמן כלשהו, דרך נקודת ההשקה של המפזר, ועד לוקטור ההתקדמות (קטע 'OB) ויוצר את הזווית $\theta$ בינו למישור ההתקדמות. נגדיר גם את הזווית המרחבית $\Omega$ הנוצרת, ולה יחידות שטח. חתך הפעולה הדיפרנציאלי מוגדר כיחס הדיפרנציאלים של חתך הפעולה והזווית המרחבית, כלומר, כיצד שינוי מזערי בחתך הפעולה משתנה כתלות בשינוי מזערי בזווית המרחבית.
נבטא את חתך הפעולה הדיפרנציאלי כפונקציה של b:
${d\sigma \over d\Omega }={2\pi bdb \over 2\pi sin(\theta )d\theta }={b \over sin(\theta )}\left|{db \over d\theta }\right|$
מביטוי זה ניתן להסיק שגידול בערכו של b מוביל לירידה בערך הזווית $\theta$, לכן, הנגזרת של השניים שלילית. מאחר שחתך הפעולה בהגדרתו הוא ערך חיובי הנגזרת במשוואה תחת ערך מוחלט. נקודה נוספת היא שהגודל הלא ידוע, המבוקש ממשוואה זו, הוא חתך הפעולה של הפיזור ( $\sigma$ ), ערך זה נמצא במונה הנגזרת. זוהי גישה מעט לא אינטואיטיבית, משום שברוב המקרים המוכרים נהוג לגזור פונקציות עם ערכים ידועים כדי להגדיר ערך שאינו ידוע.

לבסוף, בעזרת אינטגרציה של חתכי הפעולה הדיפרנציאליים בזוויות המרחביות, נוכל לחשב את חתך הפעולה של הפיזור באופן הבא:
$\sigma _{tot}=\oint d\sigma =\oint {d\sigma \over d\Omega }d\Omega$

תרשים גאומטרי של חתך פעולה לפיזור כתוצאה ממפגש החלקיק (A) עם המפזר (O). שטח החתך σ משתנה כתלות בחתך הפעולה הדיפרנציאלי, כאשר, חתך הפעולה הדיפרנציאלי הוא גודל גאומטרי המתאר את נגזרת השטח σ כתלות בזווית המרחבית - שטח Ω.

פיזור גלי-חומר

פיזור גלי-חומר כולל את פיזורם של חלקיקי חומר כמו יונים, נייטרונים ואלקטרונים. פיזור זה מתואר לרוב על ידי מכניקת הקוונטים כשינוי בפונקציית הגל כתוצאה מפגיעה במפזר. אורך הגל של חלקיקי חומר נקבע ע"פ השערת דה ברויי ותלוי בתנע שלהם. על אף שתאורטית לכל העצמים אופי גלי, במקרה של עצמים מאקרוסקופיים התופעות הגליות זניחות ולא ניתנות לתצפית.

ירי חלקיקים, כדוגמת אלקטרונים מאפשר שימוש בגלים להם אורך גל נמוך במיוחד, עובדה זו סללה את השימוש במיקרוסקופ אלקטרונים באמצעותו ניתן להבחין בעצמים קטנים שאינם ניתנים להבחנה במיקרוסקופ אור רגיל, זאת מאחר שהרזולוציה אופטית מוגבלת על ידי אורך הגל. תרומה מדעית נוספת הנזקפת לפיזור חלקיקי חומר היא פיזורם של חלקיקי אלפא על ידי גרעין האטום. פיזור מסוג זה עמד בבסיסו של ניסוי רתרפורד שהוביל לפיתוח המודל הפלנטרי לתיאור האטום.

תיאור קוונטי

הצגה קוואנטית של פיזור באמצעות מעבר בין רמות אנרגיה. דיאגרמה זו מתייחסת לסוגים שונים של פיזור אלקטרומגנטי: פיזור ריילי האלסטי ופיזור ראמאן האי-אלסטי

לפיזור הגדרה רחבה המתאימה לכל התקדמות מחזורית בזמן או במרחב. על פי מכניקת הקוונטים הגדרה זו תקפה גם עבור חלקיקי חומר, המאופיינים בפונקציית גל המתארת את החומר כהתפלגות ההסתברויות למצוא את החלקיק במרחב. לכן, פעמים רבות גל מתפזר יכול להתפרש כפיזור של חלקיק ולהפך, כפי שמתבקש, כאשר מביאים בחשבון את דואליות הגל-חלקיק. יחס דואלי זה, היוצר הקבלה בין מכניקת הקוונטים לפיזיקה הקלאסית, מלווה היבטים רבים של התהליך.

בהקבלה הקוונטית, תנועת החלקיק, המיוצגת על ידי פונקציית הגל, משתנה לאחר מהתנגשות במרכז הפיזור, כתוצאה משינוי בפוטנציאל המושרה. שינוי זה בפונקציית הגל בא לידי ביטוי מתמטי על ידי פתרון משוואת שרדינגר, כשינוי בערך העצמי של ההמילטוניאן, כלומר, במצב הקוונטי האנרגטי של הגל/חלקיק. במקרים רבים, הערכה קוונטית של הפיזור באמצעות הצגת דיאגרמת רמות אנרגיה עשויה להוות חלופה נוחה יותר לתפישת תופעת הפיזור מאשר מודל פיזיקלי קלאסי של אינטראקציית אור-חומר וזוהי אכן, לעיתים קרובות, צורת הייצוג המקובלת של תופעות כמו פיזור ראמאן.

משרעת הפיזור

תיאור סכמטי של חזית פונקציית גל מישורית הנתקלת במפזר

משרעת היא התוספת המתמטית לפונקציית הגל לאחר פגיעה עם מפזר ומתוארת לרוב על ידי הסימון הערך $f(\theta )$. פונקציה זו היא ביטוי בעל חשיבות מרכזית בתיאור הקוונטי ומקביל במובן מסוים לחתך הפעולה הגאומטרי בפיזיקה הקלאסית. בתיאור הכמותי הפשוט ביותר, נוכל להציג את הפתרון עבור פונקציית גל המתקדמת לעבר המפזר כגל מישורי:
$\psi _{0}=e^{ikz}$
כאשר גל זה ניתקל בפוטנציאל השונה מאפס בדמות מרכז פיזור מתווסף לפונקציית הגל איבר נוסף הדועך באופן רדיאלי מהמפזר החוצה:
$\psi _{0}=e^{ikz}+f(\theta ){e^{ikr} \over r}$
כדי שההסתברות למצוא את החלקיק במרחב תשמור על גודל סופי איבר זה חייב לדעוך על מנת שהאינטגרל של פונקציית הגל במרחב יתכנס ולא יהיה אינסופי.

ראוי לציין, שעבור פתרון של תוצאות ניסוייות אמיתיות, יש בדרך כלל לקחת בחשבון חבילת גלים הממוקמת במרחב ובתנע במידה סופית, בדרך כלל תוך העזרות באנליזה נומרית.

הקבלה לחתך פעולה גאומטרי

הפרשנות הקוונטית לחתך הפעולה מתבצעת על ידי יישום העיקרון שהמכפלה הפנימית או ההסתברות הכוללת נשמרת לפני ואחרי הפוטנציאל המפזר. כאשר החלקיק נע במרחב לפני המפגש עם המפזר, נחשב את דיפרנציאל ההסתברות באופן הבא:
$dP=|\psi _{0}|^{2}dV=|\psi _{0}|^{2}(vdt)d\sigma$
לאחר הפגיעה במרכז הפיזור, נוסיף לפונקציית הגל המקורית איבר נוסף עם משרעת ופאזה, המתכנס במרחק אינסופי, כך שפונקציית ההסתברות לא תתבדר באינסוף:
$\psi _{0}=e^{ikz}+f(\theta ){e^{ikr} \over r}$
דיפרנציאל ההסתברות במקרה זה יהיה:
$dP=|\psi _{0}|^{2}{f^{2} \over r^{2}}(vdt)dA=|\psi _{0}|^{2}f^{2}(vdt)d\Omega$
על מנת לשמור על הסתברות כוללת זהה לפני ואחרי הפיזור נשווה בין שני הדיפרנציאלים. מהשוואה כזו ניתן להסיק שאיבר התיקון שהוספנו לפונקציית הגל (משרעת הפיזור), שווה בגודלו (כמכפלה פנימית) לחתך הפעולה הדיפרנציאלי, הגודל הגאומטרי בו משתמשים בפתרון הקלאסי.
${d\sigma \over d\Omega }=|f(\theta )|^{2}$

פיזור אלקטרומגנטי

אחת הדוגמאות המוכרות לפיזור היא פיזור של קרינה אלקטרומגנטית הכוללת בין השאר אור נראה וגלי רדיו. פיזור של קרניים אלקטרומגנטיות הוא התופעה הפיזיקלית המרכזית, לצד בליעה, המאפשרת את ראייתם של עצמים. פיזור אופטי חיוני בשימושים כדוגמת מכ"ם, אנליזה כימית של חומרים ואיפיון גבישים בעזרת קרני X. בחיי היום-יום ניתן להבחין בפיזור אור-נראה המאפשר להבדיל בין משטחים בעלי פיזור גבוה להם מראה מט למשטחים בעלי פיזור נמוך להם מראה מבריק יותר.

הגדרה

באופטיקה, קיימות מספר הגדרות שימושיות למושג הפיזור, כאשר לעיתים נהוג לבדל תופעות כמו החזרה או העברה, ולעיתים, נהוג לסווגן כמקרים פרטיים.
במובן הכולל ביותר, ניתן להתייחס לפיזור כתופעה בסיסית בהתקדמות האור, המתארת מנעד רחב של תופעות, ביניהן החזרה והעברה. הגדרה זו מבוססת על מודל פיזיקלי קלאסי של אינטראקציית אור-חומר.
במסגרת האופטיקה הגאומטרית, לעיתים מקובל להגדיר פיזור באופן מצומצם יותר, כסך כל הקרינה שפגעה בעצם ולא עברה העברה (transmission) או בליעה (absorption). על פי הגדרה זו, שאינה כוללת העברה, גם האור המוחזר מהווה דוגמה פרטית של פיזור אלקטרומגנטי. הגדרה מקובלת נוספת ומצומצמת עוד יותר, מבדילה גם את ההחזרה כתופעה נפרדת, ומתייחסת לפיזור, כסך כל האור המוסט ממסלולי ההעברה וההחזרה. במסגרת הגדרה זו, פיזור הוא למעשה ההפרש בין כל האור המוכחד (היחלשות העוצמה הכוללת עם ההתקדמות בתווך) לבין כל האור שנבלע:
$Scattering=Extinction-Absorption$

השימוש בהגדרות השונות נובע מהצורך להבדיל תופעות המוכרות מתחום האופטיקה הגאומטרית מתופעות מיקרוסקופיות המייחדות מרכזי פיזור מסוימים.

התאוריה האלקטרומגנטית

הפתרון האנליטי לתיאור תופעת הפיזור נעשה על ידי פתרונן של משוואות מקסוול תוך שמירה על תנאי רציפות של השדה האלקטרומגנטי בין שני תווכים עם מקדם שבירה שונה. על-פי מודל זה, האור, שאינו אלא התקדמות מחזורית בזמן ובמרחב של שדה אלקטרומגנטי גורם להפרדת האלקטרונים בחומר ודיפול חשמלי. דיפול זה מהווה מקור לקרינה-שניונית, המתפזרת באופן איזוטרופי לכל הכיוונים. בגלל אופייה הגלי של קרינת האור, נוצרת התאבכות הורסת בין כלל הקרניים השניוניות למעט כיוון ההתקדמות של האור ההמעורר, כלומר, למעט העברה. ההנחה היא שבחומר הומוגני הגדול בהרבה מאורך הגל, כל גל שניוני מתבטל על ידי גל הנוצר במרחק של מחצית אורך הגל ממנו ולכן בהפרש פאזה של π. מסיבה זו פיזור אלקטרומגנטי, במובנו המצומצם (שאינו העברה או החזרה), נוטה להיות חלש יחסית במשטר האופטיקה הגאומטרית. עם זאת, ניתן למדוד הסטה משמעותית של קרני אור כאשר ההנחה הנ"ל מופרת. דוגמאות למקרים מסוימים אלה הן: פיזור אור מתמיסה דלילה של גז או נוזל, פיזור על ידי חומר לא הומוגני בו קיימות אי-רציפויות ופיזור על ידי חלקיקים קטנים בהשוואה לאורך הגל.

פיזור על ידי מפזר נע גורם להסטה בתדירות, תופעה הידועה בשם אפקט דופלר ומאפשרת את מדידת מהירות המפזר, יישום יעיל במיוחד בשימוש מכ"ם.

פיזור אלקטרומגנטי אי-אלסטי

ספקטרום אופייני של פיזור ראמאן. "פיקים" צרים בעוצמת האור המפוזר מופיעים במרחקים ייחודיים מתדירות האור המעורר, הספקטרום המוצג למשל מאפיין ננו-צינוריות פחמן (Carbon nano-tubes)

האור השניוני הנוצר כתוצאה מדיפול חשמלי הוא ברובו בעל אותה התדירות או אורך הגל של האור המעורר, מסיבה זו ניתן להסתכל עליו כתוצר של התנגשות אלסטית בה הקרן המפוזרת קיבלה את כל האנרגיה האגורה בקרן האור שהתנגשה בחומר. על כן, פיזור זה נקרא פיזור אלסטי ואליו ניתן לשייך את פיזור ריילי (Rayleigh scattering) ופיזור מיי (Mie scattering). עם זאת, כמות קטנה מהקרינה המפוזרת היא בעלת תדירות שונה מהאור הפוגע, כלומר, אנרגיה התווספה או אבדה במהלך ההתנגשות. פיזור זה מכונה פיזור אי-אלסטי והוא קטן בסדרי גודל בעוצמתו מהפיזור האלסטי. כאשר האור המתפזר הוא בעל תדירות, או אנרגיה, נמוכה מהעירור הוא נקרא פיזור סטוקס וכאשר בעל אנרגיה גבוהה יותר הוא מכונה פיזור אנטי-סטוקס

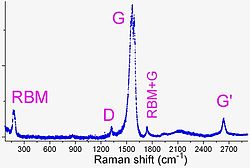
פיזור אי-אלסטי של אור מחומר התגלה על ידי ונקאטה ראמאן בשנות העשרים של המאה העשרים ותופעה זו נקראת על שמו -פיזור ראמאן (Raman scattering). חשיבותה הגדולה של תגלית זו היא בכך שפיזור ראמאן האי-אלסטי מאפשר מדידה מדויקת של מצבו הויברציוני של העצם המפזר על ידי מדידת היסט התדירות בין האור המעורר והאור המפוזר. היסט זה מתבטא בשיא (peak) צר בספקטרום של הפיזור ובהפרש תדירויות ייחודי מהאור המעורר. בכך, למעשה, מתאפשרת מדידה אופטית המאפשרת הבחנה בין חומרים שונים, כמו גם בשינויים במצב הויברציוני העשויים להתרחש כתוצאה משינויי טמפרטורה או מתיחה מכנית.
דוגמאות לפיזורים אי-אלסטיים נוספים הן פיזור ברילואן (Brillouin scattering) המתאר התנגשות אור בקוואזי-חלקיקים כמו פונונים הגורמים לשינוי בצפיפות האופטית ופיזור קומפטון (Compton scattering) המתאר פיזור אי-אלסטי של קרני X.

השפעת גודל המפזר

צבעם הכחול של השמיים הוא תוצאתו הידועה של פיזור ריילי. אור השמש מתפזר על ידי חלקיקים קטנים באטמוספירה

סיווג נוסף של המודלים המתארים פיזור או ע"פ היחס בין גודל העצם המפזר לאורך הגל של האור הפוגע, על ידי השוואה לגודל חסר ממד α המוגדר כ:
$\alpha ={\pi Dp \over \lambda }$
כאשר πDp הוא היקף החלקיק המפזר וλ הוא אורך הגל של האור הפוגע.

עבור קרניים אלקטרומגנטיות שעוברות פיזור אלסטי החלוקה נעשית באופן הבא:
1<<α (חלקיק גדול מאורך הגל) : פיזור גאומטרי
1≈α (חלקיק בעל גודל דומה לאורך הגל) : פיזור מיי (תקף לגבי מפזרים ספיריים בלבד)
1>>α (חלקיק הקטן בהשוואה לאורך הגל) : פיזור ריילי

כאשר מרכז הפיזור גדול בהרבה מאורך הגל, מקובל לשייך את הפיזור לתחום האופטיקה הגאומטרית. במקרה זה, תנועתה של הקרן נמדדת במושגים של שינויי מיקום וזווית, תופעות מאקרוסקופיות אלה (כגון החזרת ראי) לרוב אינן נקראות פיזור בטרמינולוגיה היומיומית.
לעומת זאת, כאשר מדובר על מפזרים בסדר הגודל של אורך הגל המעורר, המפזר אינו "חש" את הפרשי הפאזה של הגל המתקדם וניתן לחזות את התפלגות השדה האלקטרו-מגנטי כתוצר של אינטראקציית אור-חומר בשדה שהוא בקירוב אלקטרוסטטי. הפתרון להתפלגות זו חושב לראשונה על ידי גוסטב מיי כפתרון אנליטי של משוואות מקסוול עבור חלקיק ספירי כפונקציה של אורך הגל והמקדמים הדיאלקטריים של החלקיק והתווך בו מתקדם הגל. מאוחר יותר, פותחו פתרונות נומריים למפזרים בעלי גאומטריות מורכבות יותר כמו ספרואידים וגלילים. דוגמה ידועה לפיזור מיי למשל היא צבעם הלבן של העננים
כאשר המפזר הוא חלקיק מיקרוסקופי הקטן בסדר גודל, אחד או יותר, מאורך הגל - צורתו של המפזר מאבדת משמעות והפתרון עבור פיזור מיי מתכנס לפתרון הידוע כפיזור ריילי. הביטוי המוכר ביותר של פיזור זה בחיי היומיום הוא פיזור אור השמש על ידי חלקיקים קטנים באטמוספירה. במקרה זה, חלקה היחסי של הקרינה המפוזרת גבוה במיוחד עבור אורכי הגל הקצרים, כלומר, בחלקו הכחול של הספקטרום, והיא זו שמקנה לשמים את צבעם.

דוגמאות

• חוק בראג
• ניסוי רתרפורד
• פיזור מיי
• פיזור ראמאן
• פיזור ריילי
• פיזור קומפטון

ראו גם

שגיאות פרמטריות בתבנית:ויקישיתוף בשורה
פרמטרי חובה [ שם ] חסרים

מדיה וקבצים בנושא פיזור בוויקישיתוף

• חתך פעולה