משוואת קלאוזיוס-קלפרון

דיאגרמת פאזות T-P

משוואת קלאוזיוס-קלפרון (Clausius-Clapeyron, על שם רודולף קלאוזיוס ואמיל קלפרון) בתרמודינמיקה, היא משוואה המתארת את הקשר בין הלחץ והטמפרטורה במעבר בין שני מצבי צבירה של החומר.

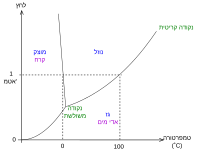
נהוג לתאר את מצבי הצבירה של החומר בדיאגרמת פאזות T-P. זהו תרשים דו-ממדי שבו ציר x מתאר את הטמפרטורה T וציר y – את הלחץ P: העקומות בתרשים מפרידות בין אזורים שמתארים מצבי הצבירה שונים של החומר: גז, נוזל ומוצק. בתנאי טמפרטורה ולחץ שנמצאים על העקומות החומר יכול להימצא בשיווי משקל בין שתי הפאזות - חלק מהחומר יהיה בפאזה אחת והשאר בפאזה האחרת. משוואת קלאוזיוס-קלפרון מאפשרת לחשב את העקומות האלה, הנקראות עקומות דו־קיום או קווי דו־קיום.

משוואת קלאוזיוס-קלפרון לקווי הדו-קיום היא:

${\frac {dP}{dT}}={\frac {L}{T\Delta \upsilon }}$

כאשר $dP/dT$ הוא השיפוע (נגזרת) של עקומת הדו-קיום, $\ L$ הוא החום הכמוס (פר חלקיק), $T$ היא הטמפרטורה ו-$\Delta \upsilon$ הוא השינוי בנפח (פר חלקיק) בעת שינוי הפאזה.

הסקת המשוואה

נניח שתי פאזות, שנסמן ב־A ו־B, שנמצאות במגע תרמי ושיווי משקל אחת עם השנייה. בתנאים האלו, הפוטנציאלים הכימיים של שתי הפאזות, מקיימים את הקשר $\mu _{A}=\mu _{B}$. מאחר שתנאי זה מתקיים בכל נקודה על עקומת הדו-קיום, תזוזה על גבי העקומה תשמור את היחס. בניסוח מתמטי, זה אומר שבתזוזה קטנה על העקומה, $d\mu _{A}=d\mu _{B}$.

אחד מקשרי גיבס-דוהם הוא

$\ d\mu =-sdT+vdP$

כאשר s ו־v הם האנטרופיה פר חלקיק והנפח פר חלקיק, בהתאמה. מהצבה במשוואה הקודמת, מתקבל הקשר:

$\ -s_{A}dT+v_{A}dP=-s_{B}dT+v_{B}dP$

ולאחר סידור מחדש, הקשר מקבל את הצורה

$\ {\frac {dP}{dT}}={\frac {s_{A}-s_{B}}{v_{A}-v_{B}}}$

בתהליך הפיך, השינוי בחום δQ נתון על ידי δQ=T dS ולכן החום שהושקע בשינוי מצב הצבירה הוא

$\ T(s_{A}-s_{B})$

וזו בדיוק ההגדרה של חום כמוס, שאותו מקובל לסמן באות $L$. הצבה של ההגדרה בקשר שקיבלנו, יחד עם הסימון $\Delta V=V_{A}-V_{B}$, נותנים

${\frac {dP}{dT}}={\frac {L}{T\Delta V}}$

שהיא משוואת קלאוזיוס-קלפרון.

הפיתוח המקורי של קלפרון

הפיתוח שהובא מקודם מבוסס על המושג של פוטנציאל כימי, אשר הוגדר כמה עשורים מאוחר יותר בהשוואה לגזירה המקורית של המשוואה בידי קלפרון. טיעונו המקורי של קלפרון מתבסס על ניסוי מחשבתי המערב מעגל קרנו שבו החומר המבצע את העבודה הוא אדים רווים, כלומר חומר שהלחץ והטמפרטורה שלו מצויים על עקומת הדו-קיום בין הפאזה הנוזלית והפאזה הגזית.

נניח שבמיכל מצויות פאזה נוזלית ופאזה גזית של חומר מסוים (עצם הקיום של שתי הפאזות במקביל זו לזו מלמד שהחומר מצוי על עקומת הדו-קיום), כשבוכנה ניידת שעליה מופעל לחץ $P$ אוטמת את המיכל מלמעלה. כעת נסתכל על ארבעה שלבים של מעגל תרמודינמי, הממומשים באמצעות הכנסת חום $q_{in}$ למערכת, הסרת משקולת זעירה שתורמת לחץ $dP$ לבוכנה, שאיבת חום $q_{out}$ והוספת משקולת שתורמת לחץ $dP$ לבוכנה. מכיוון שבמעבר פאזה חום הנכנס למערכת אינו תורם להעלאת הטמפרטורה אלא רק מגדיל את כמות החומר המצוי בפאזה הגזית, כל אחד מהשלבים במעגל הכורכים בהכנסת או הוצאת חום הוא תהליך איזותרמי (ולכן המעגל הזה הוא מעגל קרנו), ומאחר ובאדים רווים הלחץ תלוי בטמפרטורה בלבד, עולה שהאיזותרמות הללו הן גם איזוברים.

אם הכנסת החום מערבת נוזל במסה $\Delta m$, אזי מהגדרת החום הכמוס הסגולי עולה ש-: $q_{in}=L\Delta m$. שינוי נפח המיכל כתוצאה מאידוי נוזל במסה $\Delta m$ הוא $\Delta V=(v_{g}-v_{L})\Delta m$, כאשר $v_{g},v_{L}$ הם הנפחים הסגוליים של הפאזה הגזית והנוזלית. העבודה הכוללת שמבצעת הבוכנה בתהליך קרנו הזה היא לפיכך:

$W=dP(v_{g}-v_{L})\Delta m$

היחס בין העבודה הכוללת לחום שנכנס הוא נצילות המעגל, אשר לפי תוצאה מפורסמת של סאדי קרנו היא בדיוק $\eta ={\frac {dT}{T}}$. כלומר קיבלנו:

$W=\eta \cdot q_{in}\implies dP(v_{g}-v_{L})\Delta m=L\Delta m{\frac {dT}{T}}$

ושוויון זה מאפשר לחשב את שיפוע עקומת הדו-קיום של הפאזה הנוזלית והגזית כפי שמתואר בקשר קלאוזיוס-קלפרון, דהיינו:

${\frac {dP}{dT}}={\frac {L}{T(v_{g}-v_{L})}}$

יישומים

המשוואה משמשת כדי לחשב האם מעבר פאזה כלשהו יתרחש או לא.

לדוגמה, הסבר נפוץ לתופעה של החלקה על הקרח הוא כי הלחץ המוגבר של המחליק על הקרח גורם לו להנתך (להפוך ממוצק לנוזל). האם הסבר זה אכן נכון?

אם T = −2 °C אפשר להשתמש במשוואה עבור מעבר פאזה ממוצק לנוזל, ואז

${\Delta P}={\frac {L}{T\Delta V}}{\Delta T}$

ובהצבת נתונים אופייניים: L = 334 kJ/kg, T=271K, $\Delta V$ = -9.05 *10^-5m³/kg,

ואת העובדה שהלחץ גורם לשינוי ב-2 מעלות קלווין,

$\Delta T$ = 2K,

נקבל שהשינוי בלחץ יהיה

$\Delta P$ = 27.2 MPa.

השווה ללחץ שמפעיל מתאבק סומו (כ-150 ק"ג) שעומד על נעלי עקב (שטח של חצי סמ"ר)!

זהו לחץ הגדול בהרבה מהלחץ שמפעיל מחליק ממוצע על הקרח ולכן הסבר זה הוא שגוי.

ראו גם

• מצב צבירה
• טמפרטורה
• לחץ
• חום כמוס

קישורים חיצוניים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

משוואת קלאוזיוס-קלפרון34015234Q745416