חתך חרוט

הימני: היפרבולה, האמצעי: למעלה - אליפסה, למטה - מעגל, השמאלי: פרבולה.
חתך חרוט (נקרא גם חתך קוני או שניונית) הוא הצורה הגאומטרית המתקבלת כאשר מישור חותך חרוט (קונוס). צורת חתך החרוט תלויה בזווית שבה המישור חותך את החרוט.
סוגים של חתכי חרוט
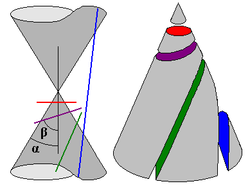
אם היא הזווית שבין ציר החרוט לקו היוצר שלו ו- היא הזווית שבין ציר החרוט למישור החותך, אזי:
מקרים מנוונים מתקבלים כאשר המישור החותך עובר דרך קודקוד החרוט: |
בגאומטריה פרויקטיבית, בהינתן שתי אלומות ישרים שביניהן התאמה פרויקטיבית, המקום הגאומטרי של חיתוך הישרים שמועתקים זה לזה הוא חתך חרוט.
על פי משפט פסקל, כל חתך חרוט נקבע באופן ייחודי באמצעות חמש נקודות שעליו, או באופן שקול, לכל חמש נקודות ישנו בדיוק חתך חרוט אחד שעובר דרך כולן. עם זאת במקרה של מעגל מספיקות שלוש נקודות, ובמקרה של פרבולה מספיקות ארבע נקודות.
הגדרות שקולות לחתכי חרוט
לחתכי חרוט יש מספר הגדרות שקולות. ההגדרות הן:
- כל צורה הנוצרת מחתך של מישור וחרוט
- היפרבולות, פרבולות, אליפסות, מעגלים, 2 ישרים, ישר ונקודה.
- בהינתן קבועים , חתך חרוט הוא אוסף כל הנקודות במישור המקיימות את המשוואה , כאשר a, b ו-c אינם כולם 0, כלומר עקום ממעלה שנייה (בדומה לכך, ישר הוא עקום ממעלה ראשונה ועקום אליפטי הוא עקום ממעלה שלישית).
- בהינתן ישר (המדריך) ונקודה (המוקד), חתך חרוטי הוא אוסף כל הנקודות כך שיחס המרחק שלהן מהמוקד ומהמדריך הוא קבוע.
לכל ההגדרות הללו יש מקרים מנוונים; ההגדרה השלישית מאפשרת לקבוצה הריקה להיות חתך חרוט, וההגדרה הרביעית לא מאפשרת למעגלים להיקרא חתוך חרוט (פרט למקרה המנוון שבו היחס הוא 0, ואז חתך החרוט הוא רק המוקד, שזה גם מעגל).
ההגדרה השנייה נבדלת מההגדרה הראשונה, בכך שכל המושגים המוזכרים מוגדרים בצורה שונה.
- אוסף הנקודות, הנמצאות במרחק קבוע מנקודה נתונה – הוא מעגל.
- אוסף הנקודות, שסכום מרחקיהן משתי נקודות נתונות הוא קבוע – הוא אליפסה.
- אוסף הנקודות, שמרחקן מנקודה נתונה שווה למרחקן מישר נתון – הוא פרבולה. בהתאם לכך אפשר להגדיר פרבולה בקלות בהגדרה 4, כשהיחס הוא 1.
- אוסף הנקודות, שהפרש המרחקים שלהן משתי נקודות נתונות קבוע – הוא היפרבולה.
הוכחה של שקילות ההגדרות הראשונה והשנייה מובאות בהמשך. קיימת עוד הוכחה הנקראת כדורי דנדלין.
מיון אלגברי של חתכי חרוט
כפי שצוין מקודם, במערכת קואורדינטות קרטזיות, המקום הגאומטרי של כל הנקודות המקיימות קשר ריבועי מסוים בשני משתנים הוא תמיד חתך חרוט (אף על פי שהוא עשוי להיות מנוון), וכל החתכים החרוטיים נוצרים בדרך הזאת. המשוואה הכללית ביותר לחתכי חרוט היא מהצורה:
כאשר כל המקדמים הם מספרים ממשיים ו-A,B,C לא כולם אפס. המשוואה הכללית הזאת היא לא בהכרח הצורה הקנונית של חתך החרוט אותו היא מייצגת, שבה הצירים הראשיים שלו מקבילים לצירי הקואורדינטות והמקדם B של האיבר המעורב מתאפס. מכאן שקשה לזהות באופן ישיר את מרכז חתך החרוט וכיוון ציריו הראשיים ממשוואה זו, ולכן היא לא תמיד נוחה לתיאור חתך החרוט. להלן נראה כיצד לעבור לצורה הקנונית ממשוואה זאת.
סימון מטריציוני
את המשוואה הריבועית לעיל ניתן לראות כסכום של שלושה פולינומים הומוגניים: התבנית הריבועית , התבנית הליניארית והאיבר הקבוע . בסימון מטריציוני ניתן לכתוב את המשוואה הכללית של חתכי חרוט כך:
הדיסקרימיננטה
טיפוס חתך החרוט (אליפסה, פרבולה או היפרבולה) נקבע על ידי החלק ההומוגני הריבועי: קיימת שמורה של התבנית הריבועית שאינה משתנה תחת טרנספורמציות סיבוב של מישור אשר ערכה מאפשר לקבוע את טיפוס חתך החרוט. שמורה זאת היא הדיסקרימיננטה של התבנית הריבועית, , שהיא גם (עד כדי קבוע ) הדטרמיננטה של המטריצה המייצגת שלה . מכיוון שהמטריצה המייצגת של התבנית הריבועית היא מטריצה סימטרית מובטח שקיימת לה מטריצה מלכסנת אורתוגונלית ולכן ניתן להביא אותה לצורה אלכסונית על ידי סיבוב מתאים של המישור; הדיסקרימיננטה של התבנית הריבועית נשמרת בתהליך משום שהדטרמיננטה של מטריצה נשמרת תחת לכסון שלה.
אם חתך החרוט אינו מנוון, אז:
- אם המשוואה מייצגת אליפסה;
- אם ו- אז המשוואה מייצגת מעגל, שהוא מקרה פרטי של אליפסה;
- אם אז המשוואה מייצגת פרבולה;
- אם אז המשוואה מייצגת היפרבולה;
- אם אז המשוואה מייצגת היפרבולה ישרה. סכום זה הוא למעשה העקבה של התבנית הריבועית, שנשמרת בתהליך הלכסון, כך שניתן לזהות מראש אם מדובר בהיפרבולה ישרה.
אלגוריתם למעבר לצורה קנונית
כאמור לעיל, הדיסקרימיננטה מאפשרת לקבוע מראש את טיפוס חתך החרוט, ולכסון המטריצה המייצגת של החלק הריבועי מאפשר למצוא טרנספורמציית סיבוב מתאימה של המישור שבה התבנית הריבועית תקבל צורה אלכסונית. ממטריצת הסיבוב ניתן לקבוע את כיוון הצירים הראשיים של חתך החרוט ביחס לצירים המקוריים, וכן לכתוב מחדש את התבנית הריבועית בצורה:
כאשר , כלומר אלו משתנים חדשים המתקבלים מהמשתנים המקוריים על ידי החלפת משתנים ליניארית, כשערכי המקדמים של החלפות משתנים אלו נקבעים ידי איברי מטריצת הסיבוב המלכסנת של התבנית הריבועית. כדי להגיע לצורה קנונית, נותר רק "להעלים" את האיברים הליניאריים במשוואה החדשה של חתך החרוט, שכעת מקבלת את הצורה:
האיברים הליניאריים מייצגים הזזה של ראשית הצירים החדשים ביחס למרכז חתך החרוט, ומכיוון שאנו מעוניינים לעבור לצורה קנונית, יש להפעיל טרנספורמציית הזזה מתאימה. זה נעשה באופן כללי על ידי הוספת קבוע לכל אחד מהמשתנים החדשים, , כאשר הקבועים נקבעים כל אחד על ידי השלמה לריבוע של הביטוי המתאים ב- ו-, ואם חתך החרוט אינו מנוון זה מוביל לצורה הקנונית:
פיתוח גאומטרי קלאסי של תכונות חתכי החרוט
ההגדרה המקורית לעקומים הריבועיים (עקומים ממעלה שנייה) הייתה עקומים המהווים חתכי חרוט, כאשר רק זמן מה לאחר גילויים הוכח שחתכי חרוט מהווים עקומים ממעלה שנייה. להלן מובאים הפיתוחים הגאומטריים הקלאסיים לתכונות הריבועיות של חתכי החרוט. הפיתוחים שמובאים כאן הופיעו לראשונה אצל אפולוניוס מפרגה, אך אפולוניוס עצמו מציין שהטיעונים שלו לא מקוריים אלא מופיעים אצל מחברים מוקדמים יותר.
פרבולה

אפולוניוס מביא הוכחה המבוססת על משפט 35 בספר השלישי של ה-"יסודות" של אוקלידס. משפט זה קובע תכונה חשובה של שני מיתרים במעגל שנחתכים: "מכפלת הקטעים שמקצה המיתר האחד על השני שווה למכפלת הקטעים שמקצה המיתר השני על הראשון". תכונה זו מועילה מאוד בניתוח העקומים נחתכים מחרוט על ידי מישור. אם נעזר במעט דמיון מרחבי, נבחין שאם נסתכל על החרוט כאוסף של פרוסות מעגליות ברדיוס משתנה, אז ניתן להיעזר במשפט כדי להסיק באופן מקומי דברים על קו החיתוך של פרוסה מעגלית כזאת עם המישור. כיוון שהעקום הנחתך סימטרי, אם נסתכל על המישור העובר דרך נקודות ו- באיור, אז נקבל אודות לסימטריה ולמשפט של אוקלידס ש-.
כעת נעזר בתכונה שחתך החרוט הפרבולי מתקבל על ידי חיתוך החרוט עם מישור שמקביל לאחד הקווים היוצרים שלו - לכן מרובע הוא מקבילית ו-. מכאן נקבל . אם ניעזר בעובדה שמשולשים ו- דומים נקבל: , במעברים האחרונים נעזרנו בדמיון משולשים וביישום המשפט של אוקלידס למעגל העובר דרך נקודות ו-. קיבלנו: ומכך נובע: כלומר יש יחס קבוע בין ריבוע הרוחב של הפרבולה בציר אחד לאורך שלה בציר השני, וזו בדיוק התכונה הריבועית של הפרבולה.
אליפסה
ניתן ליישם את צורת ההסקה הזאת גם לאליפסה, אלא שהביטוי לריבוע מחצית הרוחב של החתך החרוטי הספציפי מוחלף בביטוי מסוג אחר. אם נסתכל על הביטוי שהתקבל מהמשפט של אוקלידס במקרה הפרבולי: , אז נקבל שבמקרה של אליפסה לא ניתן להחליף את ב- שכן כאשר החרוט מתרחב מתקיים (הקו היוצר כבר לא מקביל למישור, והם מתקרבים זה לזה). כיוון שמדובר בקווים ישרים ניתן לקשר בין ל- על ידי ביטוי ליניארי מסוים, כלומר: . לכן נקבל: .
קיבלנו ש- הוא ביטוי ריבועי ב-. אם נכייל את הביטוי הריבועי כך ש- יימצא בנקודה בה מקסימלי (במינוח מודרני, נציב את ראשית הצירים במרכז האליפסה), נפטר מן החלק הליניארי של הביטוי הריבועי ונקבל: , כאשר הוא קבוע חיובי כלשהו. קיבלנו את משוואת האליפסה.
היפרבולה
בעבור המקרה ההיפרבולי נפעיל תחילה את המשוואה ל- כאשר מוצבת בקודקוד ההיפרבולה. במקרה ההיפרבולי המישור החותך מתרחק משני הקווים היוצרים ולכן הסימנים של המקדמים בביטויים הליניאריים שניהם חיוביים. לכן נקבל:
מכיוון ש-V מוצבת בקודקוד ההיפרבולה HV יהיה שווה לאפס ולכן האיבר הקבוע בביטוי הריבועי מתאפס ומקבלים:
נציב ונקבל: , וזוהי הצורה של משוואת ההיפרבולה, כאשר הפעולה של החלפה בין ל- משמעותה בעצם הצבת ראשית הצירים במרכז ההיפרבולה במקום בקודקוד שלה.
הגדרה לפי מדריך ומוקד
בהינתן ישר (המדריך) ונקודה (המוקד), חתך חרוט הוא המקום הגאומטרי של כל הנקודות שיחס המרחק שלהן מנקודה קבועה, הקרויה מוקד, ומישר קבוע, הקרוי מדריך, הוא קבוע. יחס קבוע זה קרוי אקסצנטריות.
- האקסצנטריות של אליפסה גדולה מ־0 וקטנה מ־1.
- האקסצנטריות של פרבולה היא 1.
- האקסצנטריות של היפרבולה גדולה מ־1.
המעגל הוא מקרה גבול שאינו מוגדר על ידי מדריך ומוקד במישור האוקלידי. האקסצנטריות של המעגל מוגדרת כ-0 והמוקד הוא מרכז המעגל, אך המדריך הוא הישר באינסוף במישור הפרויקטיבי.
| חתך חרוט | משוואה | אקסצנטריות |
|---|---|---|
| מעגל | ||
| אליפסה | ||
| פרבולה | ||
| היפרבולה |
היסטוריה
עבודתו של מנכמוס ועבודות אחרות
מוערך כי ההגדרה הראשונה של חתך החרוט ניתנה על ידי מנכמוס (שמת בשנת 320 לפנה"ס) כחלק מהפתרון שלו לבעיית הכפלת הקובייה הדליאנית. עבודתו לא שרדה, והשמות בהם הוא השתמש כדי להתייחס לחתכי החרוט השונים אינם ידועים. עבודתו ידועה רק באמצעות מקורות משניים. האופן שבו סיווג מנכמוס את חתכי החרוט שונה מהשיטה המודרנית. חרוטים נוצרו על ידי סיבוב משולש ישר-זווית סביב אחד מניצביו כך שהיתר שלו ייצור את פני המשטח החרוטי (היתר נקרא קו יוצר). חרוטים חולקו לשלוש מחלקות לפי זווית הראש שלהם (שנמדדת כפעמיים הזווית בין היתר לניצב שסובבים סביבו במשולש ישר הזווית המקורי). חתכי החרוט נקבעו על ידי חיתוך החרוטים האלה עם מישור שניצב לאחד הקווים היוצרים שלהם. סוג החתך החרוטי נקבע אז לפי סוג החרוט, כלומר לפי זווית הראש של החרוט; אם זווית הראש היא חדה אז החתך יהיה אליפטי; אם הזווית ישרה אז החתך יהיה פרבולי; ואם הזווית קהה הוא יהיה היפרבולי.
מקורות קדומים מייחסים לאוקלידס כתיבה של ארבעה ספרים על חתכי חרוט אך אלו גם אבדו. ידוע שארכימדס חקר חתכי חרוט, וקבע את השטח התחום על ידי פרבולה ומיתר שלה בחיבורו תרבוע הפרבולה. תחום העניין המרכזי שלו היה בקביעת שטחים ונפחים הקשורים לחתכי חרוט וחלק מעבודתו שרד בספרו על גופי סיבוב של חתכי חרוט, על קונואידים וספרואידים.
אפולוניוס מפרגה

ההתקדמות הגדולה ביותר בחקר חתכי החרוט ביוון העתיקה היא הודות לאפולוניוס מפרגה (שמת בשנת 190 לפנה"ס), אשר חיבורו בעל שמונת הכרכים "חתכי חרוט" או "הקוניקה" סיכם והוסיף רבות על הידע הקיים. חקירותיו של אפולוניוס את התכונות של חתכי החרוט הראו שכל מישור שחותך חרוט כפול, וללא קשר לזווית הראש של החרוט, יפיק חתכי חרוט בהתאם להגדרה הקודמת שלהם. בפרט, מעגלים, שאינם ניתנים לבנייה בשיטה הקודמת, גם הם ברי השגה בשיטה הזאת.
פאפוס מאלכסנדריה (שמת בשנת 350 לספירה) הוא הראשון שזיהה במפורש ודן באריכות במושג המוקד של חתך חרוט, כמו גם במושג הקשור של מדריך ("directrix"), דיון שכלל בתוכו גם את המקרה של פרבולה (שנעדר מעבודותיו הידועות של אפולוניוס). בכך פאפוס הדגים את הזהות של חתכי החרוט עם ההגדרות הגאומטריות הקלאסיות של האליפסה, הפרבולה וההיפרבולה כמיקומים גאומטריים.
העולם האיסלמי
עבודתו של אפולוניוס תורגמה לערבית, וחלק ניכר ממנה שרד עד ימינו רק בגרסה הערבית. מתמטיקאים ערבים מצאו יישומים של התאוריה, במיוחד המתמטיקאי והמשורר הפרסי עומר כיאם, אשר מצא שיטה גאומטרית לפתרון משוואות ממעלה שלישית באמצעות חתכי חרוט.
כמאה שנים קודם לעבודתו של כיאם, Abu al-Jud השתמש בחתכי חרוט כדי לפתור משוואות ממעלה רביעית ושלישית, על אף שהפתרון שלו לא עסק בכל המקרים.
מכשיר לשרטוט חתכי חרוט תואר לראשונה בשנת 1000 לספירה על ידי Al-Kuhi.
אירופה

יוהנס קפלר הרחיב את התאוריה של חתכי חרוט באמצעות "עקרון הרציפות" וגרסה מוקדמת למושגים של גבולות, והשתמש לראשונה במונח "פוקוס" כדי לכנות את המוקד של חתך החרוט, ב-1604.
ז'יראר דזארג' ובלייז פסקל פיתחו תאוריה חדשה של חתכי חרוט באמצעות צורה מוקדמת של גאומטריה פרויקטיבית, ועבודתם סייעה להתניע מחקר של התחום החדש המתהווה הזה. באופן ראוי לציון, פסקל גילה משפט המכונה "המשושה המיסטי" (hexagrammum mysticum), אשר ממנו ניתן היה להסיק תכונות רבות אחרות של חתכי חרוט.
רנה דקארט ופייר דה-פרמה יישמו שניהם את הכלי החדש של הגאומטריה האנליטית שפיתחו לחקר חתכי חרוט. יישום זה איפשר להמיר את הבעיות הגאומטריות של חתכי חרוט לבעיות באלגברה. עם זאת, זה היה ג'ון ואליס אשר בחיבורו מ-1655 "Tractatus de sectionibus conicis" הגדיר לראשונה את חתכי החרוט כמשוואות אלגבריות ממעלה שנייה.
חתכי חרוט בפיזיקה
חתכי חרוט מופיעים במכניקה כפתרונות האפשריים של בעיית קפלר.
ניוטון מצא כי מסלולם של כוכבי הלכת חייב להיות אחד מחתכי החרוט – מעגל, אליפסה, פרבולה או היפרבולה. הוא מצא כי אם כוכב לכת יגדיל בצורה מלאכותית את מהירותו עד כדי הגעה למהירות גבולית מסוימת, מסלולו יהפוך מאליפטי לפרבולי. אם מהירותו תהיה גבוהה עוד יותר מהמהירות הגבולית, מסלולו יהיה היפרבולי. הן המסלול הפרבולי והן המסלול ההיפרבולי הם מסלולים פתוחים – כלומר, גופים שינועו בהם יתרחקו מהשמש לבלי שוב.
ראו גם
קישורים חיצוניים
- עמוס אלטשולר, חתכי החרוט בגישה סינתטית, (הוכחות קלאסיות לעקומים המתקבלים על ידי חתכי החרוט), על"ה - עלון למורי המתמטיקה, גיליון 9, ספטמבר 1991.
- מיכאל קורן, חתכי חרוט, הוכחה באמצעות תכונות הווקטורים
- חתך חרוט, באתר MathWorld (באנגלית)
- חתך חרוט, באתר אנציקלופדיה בריטניקה (באנגלית)
 חתכים חרוטים, דף שער בספרייה הלאומית
חתכים חרוטים, דף שער בספרייה הלאומית
חתך חרוט40105479Q124255