משפט הקוסינוסים
.gif)
משפט הקוסינוסים הוא משפט טריגונומטרי שמציין את הקשר בין צלעות משולש לאחת מזוויותיו. המשפט הוא הכללה של משפט פיתגורס למשולש כלשהו.
עבור משולש שצלעותיו הן $ a,b,c $ והזווית שמול $ c $ היא $ \gamma $ , משפט הקוסינוסים קובע:
- $ {\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos(\gamma )} $
משפט פיתגורס מתקבל במקרה הפרטי שבו $ \gamma =90^{\circ } $ ולכן $ c^{2}=a^{2}+b^{2} $ .
היסטוריה
משפט הקוסינוסים מופיע כבר בספר 'יסודות' של אוקלידס מהמאה ה-3 לפנה"ס. הספר מכיל גרסה גאומטרית, ללא שימוש בפונקציות טריגונומטריות (כיוון שטרם הוגדרו). המשפט מופיע בכרך 2 של ה'יסודות' כמשפט 12 עבור משולש קהה-זווית וכמשפט 13 עבור משולש חד-זווית.
בציור משמאל, גרסת המשפט עבור משולש חד-זווית: $ BC^{2}+AC^{2}=AB^{2}+2S_{\color {blue}DHIC} $ .
מכיוון ש-$ S_{\color {blue}DHIC}=BC\cdot AC\cdot \cos(ACB) $ מתקבל משפט הקוסינוסים בגרסתו המוכרת. גרסה זו נוסחה בימי הביניים בעקבות פיתוחו של ענף הטריגונומטריה על ידי מתמטיקאים מוסלמים.
בתחילת המאה ה-10 האסטרונום והמתמטיקאי המוסלמי אל-בתאני הכליל את המשפט לגאומטריה ספירית. הכללה זו אפשרה לו לחשב את המרחק הזוויתי בין כוכבים.
המתמטיקאי ג'משיד אל-קאשי מסמרקנד בן המאה ה-15 חישב ערכים של פונקציות טריגונומטריות. חישוביו הפכו את משפט הקוסינוסים ממשפט תאורטי למשפט שימושי. בצרפתית משפט הקוסינוסים נקרא משפט אל-קאשי.
הוכחות
הוכחה טריגונומטרית
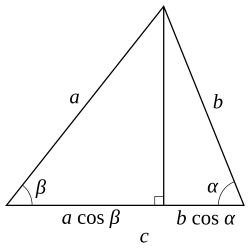
- נעביר גובה לצלע $ c $ (ראו ציור משמאל) $ c=a\cos(\beta )+b\cos(\alpha ) $
- (השוויון נכון גם עבור משולש קהה זווית. שם האנך חותך את $ c $ מחוץ למשולש וקוסינוס הזווית הקהה הוא שלילי).
- נכפיל את השוויון הקודם ב-$ c $ ונקבל $ c^{2}=ac\cos(\beta )+bc\cos(\alpha ) $ .
- באותו אופן מקבלים $ a^{2}=ac\cos(\beta )+ab\cos(\gamma )\ ,\ b^{2}=bc\cos(\alpha )+ab\cos(\gamma ) $ .
- מחיבור שתי המשוואות הנ"ל נקבל $ a^{2}+b^{2}=ac\cos(\beta )+bc\cos(\alpha )+2ab\cos(\gamma ) $ .
- לאחר העברת אגפים נקבלל $ ac\cos(\beta )+bc\cos(\alpha )=a^{2}+b^{2}-2ab\cos(\gamma ) $ .
- לפי השלב השני בהוכחה, אגף שמאל של המשוואה האחרונה שווה ל-$ c^{2} $ ומתקבל משפט הקוסינוסים: $ c^{2}=a^{2}+b^{2}-2ab\cos(\gamma ) $ .
הוכחה זו כאמור, נכונה עבור משולש כלשהו. בהוכחות רבות הנעזרות בטריגונומטריה, נעשית הפרדה בין משולשים חדי-זווית למשולשים קהי-זווית.
שימוש במשפט פיתגורס
ניקח משולש בעל צלעות $ a,b,c $ ובעל זוויות $ \alpha ,\beta ,\gamma $ ממול לכל צלע בהתאמה. נוריד גובה מקודקוד הזווית $ \beta $ לצלע $ b $ . את המשוואה נקבל באמצעות משפט פיתגורס על המשולש ישר הזווית השמאלי:
- $ {\begin{aligned}c^{2}&={\bigl (}a\sin(\gamma ){\bigr )}^{2}+{\bigl (}b-a\cos(\gamma ){\bigr )}^{2}\\&=a^{2}\sin(\gamma )^{2}+b^{2}-2ab\cos(\gamma )+a^{2}\cos(\gamma )^{2}\\&=a^{2}{\bigl (}\sin(\gamma )^{2}+\cos(\gamma )^{2}{\bigr )}+b^{2}-2ab\cos(\gamma )\\&=a^{2}+b^{2}-2ab\cos(\gamma )\end{aligned}} $
היות ש: $ \sin(\gamma )^{2}+\cos(\gamma )^{2}=1 $ .
שימוש במשפט תלמי
את $ \triangle ABC $ שצלעותיו $ BC=a,AC=b,AB=c $ , נחסום במעגל, כפי שניתן לראות בשרטוט משמאל.
נבנה $ \triangle ABD $ החופף למשולש המקורי: $ AD=BC,BD=AC $ . מהקודקודים $ C,D $ נעביר גבהים החותכים את הצלע $ AB $ בנקודות $ E,F $ בהתאמה.
- $ {\begin{aligned}&BF=AE=BC\cos(\sphericalangle CBA)=a\cos(\sphericalangle CBA)\\&DC=EF=AB-2BF=c-2a\cos(\sphericalangle CBA)\end{aligned}} $
כעת, ממשפט תלמי נקבל:
- $ {\begin{aligned}&AD\cdot BC+AB\cdot DC=AC\cdot BD\\&a^{2}+c{\bigl (}c-2a\cos(\sphericalangle CBA){\bigr )}=b^{2}\\&a^{2}+c^{2}-2ac\cos(\sphericalangle CBA)=b^{2}\end{aligned}} $
שימוש באנליזה וקטורית
את המשפט קל להוכיח באמצעות חשבון וקטורים. וקטור הוא גודל לינארי מופשט הקיים במרחב וקטורי. על וקטורים במישור $ \mathbb {R} ^{2} $ ניתן לחשוב כעל חצים בעלי אורך וכיוון, ובאמצעותם לייצג צורות גאומטריות, ובפרט מצולעים כגון משולש.
קל לראות מהאיור כי $ {\vec {c}}={\vec {a}}-{\vec {b}} $ .
נשתמש במכפלה סקלרית ונקבל:
- $ c^{2}={\vec {c}}\cdot {\vec {c}}=({\vec {a}}-{\vec {b}})\cdot ({\vec {a}}-{\vec {b}})={\vec {a}}\cdot {\vec {a}}+{\vec {b}}\cdot {\vec {b}}-2{\vec {a}}\cdot {\vec {b}}=a^{2}+b^{2}-2ab\cos(\gamma ) $
שכן הזווית $ \gamma $ שמול הצלע $ c $ במשולש שווה לזווית בין הווקטורים $ {\vec {a}},{\vec {b}} $ (שכן הן זוויות בין ישרים מקבילים הנוצרים מהעתקה מקבילה של הווקטור $ {\vec {b}} $).
ראו גם
קישורים חיצוניים
- משפט הקוסינוסים, באתר MathWorld (באנגלית)
