עצמים קונצנטריים
יש להשלים ערך זה: בערך זה חסר תוכן מהותי.
| ||
| יש להשלים ערך זה: בערך זה חסר תוכן מהותי. | |
יש לערוך ערך זה. הסיבה היא: ויקיזציה.
| ||
| יש לערוך ערך זה. הסיבה היא: ויקיזציה. | |
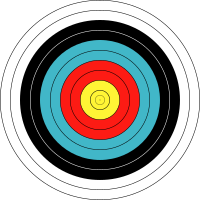

עצמים קונצנטריים הם עצמים בעלי מרכז משותף (קונצנטריות היא מחזור, חוג בתוך חוג), עצמים אלה עשויים להיות דומים זה לזה (למשל: סדרה של מעגלים קונצנטריים), או שונים זה מזה, אך בכל זאת בעלי מרכז משותף (למשל: סדרה של מצולעים משוכללים החסומים כולם במעגל נתון). במישור עצמים קונצנטריים אינם חופפים, אך במרחב תלת-ממדי ייתכנו עצמים דו-ממדיים קונצנטריים וחופפים (למשל: אוסף מעגלים העוברים דרך הקוטב הצפוני והקוטב הדרומי - לכולם מרכז משותף, שהוא מרכז כדור הארץ).
פגיעת אבן במאגר מים יוצרת גלי רוחב, הנראים כמעגלים קונצנטריים שמרכזם הוא מקום פגיעת האבן במים.
סמלים
- מעגלים קונצנטריים מופיעים בסמליהם של חילות אוויר רבים, ובהם חיל האוויר הצרפתי וחיל האוויר המלכותי.
- בלוח התמרורים הישראלי מצוין מרכז העיר או האזור בסמל שבו מעגלים קונצנטריים אחדים.[1]
- סמל תנועת סובוד מורכב משבעה מעגלים קונצנטריים, חתוכים לשבע גזרות.
בספרות התורנית

התוספות במסכת סוכה[2] מציגים שיטה לחישוב שטח העיגול: בתוך המעגל יוצרים בחוטים סדרה של מעגלים קונצנטריים, ממרכז העיגול ועד שפתו. את סדרת המעגלים חותכים ברדיוס שלו. ייווצרו לנו חוטים רבים, כאשר הראשון הוא הכי ארוך, וכל אחד ואחד פוחת אורכו מעט מקודמו. לאחר יישור החוטים נוצר משולש שווה-שוקיים. את המשולש חותכים מהקודקוד לבסיס, ואת שני המשולשים שנוצרים הופכים ויוצרים מהם מלבן. שטח המלבן (אורך כפול רוחב) הוא שטח העיגול. למעשה הנוסחה לחישוב השטח המוצגת כאן היא היקף כפול רדיוס חלקי שתיים. השיטה המוצגת בתוספות היא שיטתו של רבי אברהם בר חייא.
בגאולוגיה
עצמים קונצנטריים מופיעים גם בגאולוגיה כדוגמה נמנה את: פסי הזרימה שהם פסים המופיעים על סלעים ונראים לאחר ביקועם, דייק שהוא סלע מגמטי שנוצר לאחר חדירת מגמה לשכבת הליתוספירה וים הגשמים שהוא מישור בזלת גדול על הירח.
באדריכלות
מטרופולין. צ'וגה זנביל. רובע התעלות מהמאה ה-17 באמסטרדם. נווה שאנן (תל אביב).
בבוטניקה
קישורים חיצוניים
- עצמים קונצנטריים, באתר MathWorld (באנגלית)
הערות שוליים
- ↑ לוח התמרורים, באתר של משרד התחבורה, עמ' 72
- ↑ תלמוד בבלי, מסכת סוכה, דף ח' עמוד א'
עצמים קונצנטריים39185758
