דמיון (גאומטריה)
בגאומטריה, דמיון של עצמים פירושו שלשני העצמים יש אותה צורה בדיוק, אך גודל שונה. במילים אחרות, ניתן לקבל אחד מהם על ידי הגדלה או הקטנה של האחר, כלומר להביא למצב של חפיפה בין הצורות. בניסוח פורמלי, עצמים דומים הם עצמים חופפים עד כדי הגדלה או הקטנה, כלומר הכפלת כל הגדלים במספר קבוע. בדרך כלל מדברים על מצולעים דומים.
אם שתי צורות דומות, אז כל הזוויות המתאימות שוות, ההיקפים, הצלעות המתאימות וקווים מיוחדים (לדוגמה גבהים) נמצאים באותו יחס, והשטחים (של כל הצורה או של חלק ממנה, המוגדר באותו אופן בשתי הצורות) נמצאים ביחס הזה בריבוע. ניתן לדבר גם על גופים תלת-ממדיים דומים, ואז הנפחים נמצאים ביחס הזה בשלישית.
דמיון עצמי הוא מקרה בה צורה דומה לחלק של עצמה. צורה שיש לה דמיון עצמי בכל רמת קרבה היא פרקטל. בהשאלה, כל מערכת מתמטית שמכילה עותק של עצמה נקראת "דומה עצמית".
יחס הדמיון הוא יחס שקילות, ובמסגרתו כל המעגלים דומים זה לזה, כל הריבועים דומים זה לזה וכו'. חפיפה היא מקרה פרטי של דמיון, המתקבל כאשר היחס שווה ל-1.
דמיון משולשים
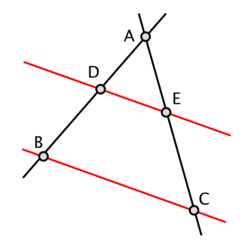
ערך מורחב – דמיון משולשים
דמיון משולשים הוא השימוש הנפוץ ביותר בדמיון בין צורות. יש משפטים רבים המוכיחים כי שני משולשים הם דומים, אבל החשוב מכולם הוא משפט תאלס, האומר: (בהינתן שהזווית על A נשארת קבועה) אם ורק אם הקווים הבאים הם מקבילים אם ורק אם . אז, מכאן נובע שזוויות של 2 משולשים הן זהות אם ורק אם היחסים בין הצלעות המתאימות זהות.
דמיון מרובעים
דמיון מרובעים לא נפוץ כל כך כמו דמיון המשולשים, אך גם בו ניתן לעשות שימוש במתמטיקה. על מנת להוכיח דמיון מרובעים יש לחתוך את המרובעים לשני משולשים על ידי אלכסון ולדמות את המשולשים שנוצרו בהתאמה. יש לשים לב שהמרובעים דומים אך ורק אם הצלעות השוות במשולשים שנוצרו (האלכסון) מתאימות בהדמיה לצלעות השוות במשולשים שנוצרו במרובע השני ואך ורק אם צלעות סמוכות במרובע זה לא נגדיות במרובע השני. ניתן באותה דרך להוכיח דמיון של מצולע עם n צלעות על ידי חיתוך לn - 2 משולשים דומים.
קישורים חיצוניים
30135919דמיון (גאומטריה)