עקומת מאמץ-עיבור

איור מס' 1: עקומת מאמץ-מעוות מציגה התנהגות אופיינית של הכניעה עבור מתכות אל ברזליות. המאמץ $(\sigma )$ מוצג כפונקציה של העיבור $(\epsilon )$ .
1: קצה הגבול האלסטי ליניארי
2: חוזר לכניעה מוסט (0.2% חוזק מוכח)

עקומת מאמץ מעוות היא הקשר בין המאמץ והעיבור שחומר מקיים. עקומה זו ייחודית עבור כל חומר. היא נוצרת על ידי מדידת המעוות (עיבור) במרווחים שונים אל מול מגוון העמסות (מאמצים). עקומה זו מספקת מספר מאפיינים קריטיים עבור החומר המוצג, כולל מידע בנוגע למודול האלסטיות.^[1]

באופן כללי, לעקומות המייצגות את קשר בין מאמץ לבין עיבור בדפורמציות שונות, ניתן להתייחס כעקומות מאמץ-מעוות. המאמץ והעיבור יכולים להיות בכיוונים שונים, מאמצים נורמלים (חד ציריים בכיוון האורכי של הדגם הנמדד), מאמצי גזירה, או שילוב שלהם. יכולים להיות שילובים כמו מאמץ לא ציריים, שני צירים, מאמצים מרובי צירים או אפילו מאמצים תלויי זמן. צורת הדפורמציה יכולה להיות: מתיחה, דחיסה, פיתול, סיבוב, וכן הלאה. אם לא נכתב אחרת, עקומת מאמץ-מעוות תתייחס לקשר בין מאמץ חד צירי נורמלי לבין עיבור חד צירי נורמלי של חומרים הנמדדים בניסוי זה.

ניסוי המתיחה מתבצע כך שניקח דגם בעל מידות חתך ידועות- A ונפעיל כח F בניצב לו משני צידי הדגם. הדגם/חומר יחווה מאמץ המוגדר להיות היחס בין הכוח חלקי שטח החתך, כמו גם הארכה צירית, אלסטית ופלסטית בחומרים משיכים.

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{\sigma} = \tfrac{F}{A_0}}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{\epsilon} = \tfrac{L-L_0}{L_0} = \tfrac{\Delta L}{L_0}}

הכתב התחתי '0' מציין את המידות המקוריות של הדגם. מאמץ ביחידות SI מסומן בפסקל (הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle Pa=\frac{N}{m^2}} ) ועבור עיבור הוא חסר יחידות כלומר השינוי הוא באחוזים יחסית לאורך ההתחלתי. עקומת מאמץ-מעוות עבור חומר כלשהו תציג את התארכות הדגם ואת השינוי האורכי שחל בו עד שבירת הדגם. בעקרון העיבור הוא בכיוון האופקי (הצרות הדגם) והמאמץ בכיוון הניצב. יש לשים לב שעבור שימושים הנדסיים, נציג את המאמץ יחסית לעיבור עבור שטח החתך ההתחלתי בלבד לכל אורך תהליך הדפורמציה. ישנה בעייתיות מסוימת כיוון שהשטח הנ"ל אינו השטח האמיתי, כיוון ששטח החתך קטן כאשר מתבצעת דפורמציה אלסטית או פלסטית. העקומה המתחשבת בשטח החתך הראשוני נקראת "עקומת מאמץ-מעוות הנדסית" ואילו העקומה אשר מתחשבת בשטח החתך המשתנה נקראת: "עקומת מאמץ-מעוות אמיתית". היחסים בין שתי העקומות יתבררו בהמשך.

שלבים

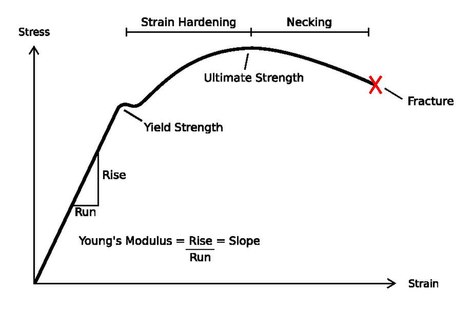
דיאגרמה סכמטית של העקומה עבור פלדה פחמנית מוצגת באיור מס' 2. ישנם מספר שלבים המציגים התנהגות וממחישים מאפיינים מכניים שונים. יש צורך לציין כי לא כל החומרים עוברים את כל השלבים וחלקם 'מדלגים' על אחד או יותר מהשלבים המוצגים באיור או אפילו מתנהגים בצורה שונה לחלוטין.

השלב הראשון הוא השלב האלסטי. המאמץ הוא פרופורציונלי לעיבור, הוא תואם לחוק הוק וערך השיפוע שווה למודול האלסטיות (יאנג). בשלב זה החומר חווה עיוות אלסטי בלבד, סיום השלב הראשון מתרחש כאשר החומר מתחיל לחוות עיוות פלסטי. המאמץ בנקודת המעבר בין המעוות האלסטי למעוות הפלסטי מוגדר כ'חוזק לכניעה'.

השלב השני הוא שלב הקשיית המעוותים. השלב מתחיל לאחר נקודת הכניעה ומסתיים בנקודת המאמץ האולטימטיבי' המאמץ המקסימלי בעקומת המאמץ-מעוות. בשלב זה המאמץ עולה לאורך כל החומר, אולם ישנו חלק שטוח (ובמקרים מסוימים שיפוע מתון מטה). החלק הנמוך ביותר של העקומה במקרה זה נקרא 'נקודת הכניעה התחתונה', תהליך זה נקרא 'מעוות לודר' (Luders) המאמץ הדרוש לנוקלאציה של רצועת לודר גבוה יותר מהמאמץ הדרוש להתקדמותו. רצועת לודר גורמת לכך שהדפורמציה הפלסטית תתקדם בצורה שווה לאורך כל הדגם. לאחר שהדגם בעל דפורמציה אחידה לכל אורכו, עליית המאמץ ביחד עם התארכות הדגם יוצרים מצב של הקשיית מעוותים. הקשיית מעוותים משמעה, יצירת מעוותים חדשים והעלאת הצפיפות הכללית שלהם יוצרים התנגדות לתנועת הנקעים. על מנת להתגבר על התנגדות זו יש צורך בהפעלת מאמץ גבוה יותר. ככל שהעיבור עולה, הקשיית המעוותים מתגברת עד שהמאמץ מגיע למאמץ המקסימלי ( Tensile Strength).

השלב השלישי, הוא שלב היווצרות הצוואר. לאחר המעבר על פני המאמץ המקסימלי, צורת צוואר נוצרת, אזור בו רוחב החתך חווה הצרה יחסית לרוחב הממוצע של שאר הדגם. חוזק הדגם באזור דפורמציית הצוואר משתנה וחזק יותר היכן ששטח החתך קטן יותר. התגובה הזו גורמת להיווצרות והתפשטות צווארתיות באזורים הצמודים לצוואר ובמהרה גם לשבר. יש לשים לב כי אמנם כח המתיחה יורד אך הקשיית המעוותים ממשיכה להתרחש, כך שהמאמץ האמיתי אף על פי שהמאמץ ההנדסי יורד בגלל היווצרות הצוואר והקטנת שטח החתך. השלב מסתיים בשבר, לאחר השבר ניתן למדוד את התארכות הדגם ואת הקטנת שטח החתך.

הקשר בין עקומת מאמץ-מעוות הנדסי למאמץ אמיתי

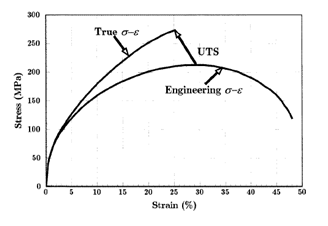
איור מס' 3: ההבדל בין עקומת מאמץ-מעוות אמיתית לבין עקומת מאמץ-מעוות הנדסית.

כיוון שמתרחשת הצטמקות של שטח החתך והתעלמות ההתפתחות האורכית, קיים שוני בין עקומת מאמץ-מעוות הנדסית לבין עקומת מאמץ-מעוות אמיתית. הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{\sigma_t} = \tfrac{F}{A}}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{\epsilon_t} = \int\tfrac{\delta L}{L}}

תחת הנחת שימור נפח לאורך כל התהליך ודפורמציה אחידה על פני כל הדגם ניתן לכתוב:

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle A_0 L_0=AL}
עבור המאמץ והמעוות האמיתיים ניתן להשתמש במאמץ-מעוות ההנדסיים:

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{\sigma_t} = \tfrac{F}{A}=\tfrac{F}{A_0} * \tfrac{A_0}{A} = \tfrac{F}{A_0} * \tfrac{L}{L_0}=\sigma(1+\epsilon)}

עבור עיבור אמיתי, נוכל לגזור ולבטא את השינוי בעיבור:

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{\delta \epsilon_t} = \tfrac{\delta L}{L}}

נבצע אינטגרציה עבור שני הצדדים ונחיל את תנאי השפה:

$\epsilon _{t}=\int \limits _{L_{0}}^{L}{\delta {L} \over L}$

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{\epsilon_t} = ln(\tfrac{L}{L_0})=ln(1+\epsilon)}

בשל כך, בניסוי מתיחה, מאמץ אמיתי גדול יותר ממאמץ הנדסי ועיבור אמיתי קטן מעיבור הנדסי. עקומת המאמץ מעוות האמיתית נעה למעלה ושמאלה החל מהשלב השני בעקומה. ההבדל בין המאמץ-מעוות האמיתי לבין המאמץ-מעוות הנדסי עולה עם התפתחות המעוות הפלסטי. בעיבורים נמוכים (באזור האלסטי בעיקר) ההבדלים בין העקומות זניחים. נקודת החוזק המתיחה בעקומה ההנדסית היא מיוחדת ונקראת המאמץ המקסימלי אך היא אינה באה לידי ביטוי ולא מבדילה בין שלב לשלב בעקומה האמיתית. כיוון שמאמץ הנדסי פרופורציוני לכח המופעל על הדגם הקריטריון להופעת צוואר הוא: הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{\delta \textit F} =0} .

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{\delta \textit F} =0=\sigma_t \delta A + A \delta\sigma _t }

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{-\tfrac {\delta A}{A}} = \mathrm {\tfrac{\delta \sigma _t }{\sigma _t}}}

ביטוי זה מציע שיווי משקל טבעי עבור מאמץ מקסימלי. אפקט הקשיית המעוותים מאוזן על ידי התכווצות השטח בנקודת המאמץ המקסימלי. לאחר יצירת הצוואר בדגם, הדפורמציה בדגם הטרוגנית ולא אחידה ולכן הביטוי לעיל אינו תואם לשלב השלישי. המאמץ והמעוות האמיתיים לאחר המעבר על פני המאמץ המקסימלי בעקומה הנדסית או לאחר השלב בו ניתן להניח שימור נפח באים לידי ביטוי בצורה הבאה:

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{\sigma_t } = \tfrac{F}{A_{neck}}}

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{\epsilon_t} = ln(\tfrac{A_0}{A_{neck}})}

משוואה אמפירית המתארת את הקשר בין המאמץ והמעוות האמיתיים היא:

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{\sigma_t} = K (\epsilon_t)^n}

כאשר n הוא מקדם הקשיית מעוותים, הוא מודד את התנהגות החומר בקשר להופעת מעוותים. חומרים בעלי ערך n גבוה יותר יהיו חומרים בעלי התנגדות להופעת צוואר בצורה משמעותית יותר. בדרך כלל מתכות בטמפ' החדר יהיו בטווח 0.02-0.05 עבור הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} .^[2] K הוא מקדם חוזק עבור החומר.

סיווג חומרים

ניתן להבחין במספר קריטריונים משותפים כאשר מתבוננים בעקומת מאמץ מעוות עבור קבוצות חומרים שונות. על בסיס זה ניתן לחלק את החומרים לשתי קטגוריות רחבות: חומרים משיכים וחומרים פריכים.^[3]

שגיאה ביצירת תמונה ממוזערת:

עקומת מאמץ מעוות של פלדה מבנית
1: מאמץ אולטימטיבי/מקסימלי
2: נקודת כניעה
3: שבר
4: שלב הקשיית מעוותים
A: מאמץ הנדסי
B: מאמץ אמיתי

חומרים משיכים

חומרים משיכים הכוללים פלדה מבנית וכן סגסוגות רבות של מתכות אחרות. מוגדרים על ידי היכולת שלהם לעבור את נקודת הכניעה בטמפ' רגילות.^[4]

פלדות דלות פחמן יציגו בדרך כלל קשר ליניארי מאוד בין המאמץ למעוות עם נקודת כניעה ברורה (איור מס' 2). החלק הליניארי של העקומה הוא החלק האלסטי והשיפוע הוא מודול האלסטיות- מודול יאנג. חומרים משיכים כוללים בתוכם מספר מתכות, פולימרים, חומרים קרמיים המציגים נקודת כניעה. זרימה פלסטית של החומר מתחילה לאחר נקודת הכניעה העליונה וממשיכה לאחר המעבר בנקודת הכניעה התחתונה. בנקודת הכניעה התחתונה דפורמציה הטרוגנית קבועה מתרחשת על פני הדגם. רצועת הדפורמציה שהחלה בנקודת הכניעה העליונה מתפשטת כך שבנקודת הכניעה התחתונה הדפורמציה אחידה ומתחילה זרימה פלסטית לאורך כל הדגם. הרצועה מתפשטת והיא נגרמת כחלק מתופעת מעוותי לודר. לאחר נקודה זו מתחילה תופעת הקשיית המעוותים. תופעה זו קשורה בד בבד עם היווצרות נקעים במערכת. לדוגמה, הדפורמציה מתפשטת אך נתקלת בנקעים המתנגדים לתנועה ולכח ובכך מאטים את התקדמות הדפורמציה. בגלל תופעת ההקשייה המאמץ הנדרש לתנועת הנקעים יהיה גדול, לאחר המעבר על פני הנקעים המאמץ הנדרש להמשך הדפורמציה יקטן.

לאחר נקודת הכניעה, העקומה תעלה בשיפוע מתון יותר כיוון שיש צורך להתגבר על שחרור הנקעים מתוך אתרי הסריג [אנ']. בהמשך הדפורמציה המאמץ עולה תוך כדי התחשבות בהקשיית המעוותים, עד שזה מגיע למאמץ המקסימלי (Ultimate Tensile Stress). בנקודה זו נפסקת התכווצות שטח החתך בהתאם ליחס פואסון, בשטח החתך של נקודת השבר נוצר צוואר שמוביל בסופו של דבר לשבר.

תופעת הצוואר בדגם במהלך הניסוי קשורה לאי יציבות גאומטרית בדגם. בשל המבנה הלא הומוגני לחלוטין של כל חומר, וכיוון שכל דגם יכיל בתוכו פגמים סביר שנמצא אזורים בהם קיימים נקבוביות קטנות או אזורים בהם פני השטח לא מושלמים. תופעה זו מובילה לשטח חתך נמוך באותם אזורים. עבור עיבור הקטן מהעיבור בנקודת המאמץ המקסימלי הקשיית המעוותים באזורים אלו תעלה על הפחתת שטח החתך ולכן יהיה קושי מסוים ליצור דפורמציה, כך שאי היציבות הגאומטרית לא באה לידי ביטוי מתחילת המעוות הפלסטי. לחומרים אלו יש יכולת לחפות על חוסר ההומוגניות לפני ההגעה לנקודת המאמץ המקסימלי. אולם כאשר העיבור גדל, השפעת הקשיית המעוותים יורדת. בנקודה זו האזור בעל שטח החתך הקטן יותר יהיה חלק יותר מאזורים אחרים, ההקטנה גורמת לריכוז מאמצים באזור והיווצרות הצוואר. הצוואר הופך לניכר יותר ויותר עד שהשבר מתרחש. אחרי שנוצר צוואר, הדפורמציה הפלסטית מתרכזת בצוואר בעוד ששאר הדגם עובר התכווצות אלסטית כיוון שכח המתיחה יורד.

עקומת מאמץ-מעוות עבור חומרים משיכים ניתנת להצגה על ידי משוואת ראמברג-אוסגוד.^[5] משוואה זו פשוטה ודורשת את החוזק לכניעה של החומר, מאמץ מקסימלי, מודול האלסטיות (יאנג) ואחוז ההתארכות הסופי.

חומרים פריכים

חומרים פריכים כוללים בתוכם: ברזל יציקה, זכוכית ואבן. מאופיינים בעובדה שהשבר מתרחש ללא שינוי ניכר לאורך השינוי האורכי.^[6] לעיתים נשברים לפני נקודת הכניעה התאורטית.
לחומרים פריכים כמו בטון, סיבי פחמן אין הגדרת נקודת כניעה ברורה ולא מתבצעת הקשיית מעוותים במהלך הפעלת המאמץ. לכן הגדרת המאמץ האולטימטיבי/ מקסימלי וכך גם נקודת השבירה היא לא חד משמעית. בעקומת מאמץ מעוות אופיינית כפי שניתן לראות באיור מס' 5 עבור חומרים פריכים כמו זכוכית לא מציגים דפורמציה פלסטית, אבל כושלים גם כאשר הדפורמציה היא אלסטית בלבד. אחד הקריטריונים של חומרים פריכים הוא ששני חלקי השבר מתאחדים ויוצרים צורה של הדגם המקורי כיוון שהצוואר כפי שהוא מופיע בחומרים משיכים לא מופיע. עקומת מאמץ מעוות אופיינית עבור חומרים פריכים יהיה ליניארי. עבור חומרים מסוימים כמו בטון, מאמץ המתיחה הוא זניח יחסית למאמץ הלחיצה ונחשב לאפס עבור רוב האפליקציות ההנדסיות. סיבי זכוכית הם בעלי חוזק למתיחה גבוה מפלדה אבל זכוכית בתפזורת ולא בנויה היטב מאבדת את החוזק הזה. החוזק למתיחה לא בא לידי ביטוי בזכוכית כיוון שלמקדם עוצמת הלחץ יש חשיבות כאשר מערבים את הפגמים שקיימים בחומר. ככל שגודל הדגם גדל כמות הדגמים גדלה גם כן. באופן כללי, החוזק למתיחה עבור חבל תמיד יהיה קטן יותר מאשר סכום החוזק למתיחה עבור סיב בודד.

גורמים משפיעים

עקומות מאמץ מעוות עבור חומרים שונים הן מגוונות מאוד כתוצאה ממבנים שונים ומרכיביהם. בשל גורמים חיצוניים, ניסויי מתיחה עבור אותו חומר יציג נקודות כניעה שונות בעיקר בהתאם לטמפ' הדגם ולמהירות ההעמסה במהלך הניסוי. הגבול בין גורמים פנימיים לבין גורמים חיצוניים אינו מוחלט ולא ניתן להציב גבול ברור בין הגורמים והשפעתם. גורמים רבים יכולים להשפיע על עקומת המאמץ-מעוות על ידי הגדלת החוזק לכניעה, הקשיית מעוותים, זיקון וכל אלה יכולים לשנות את המבנה, את המרכיבים של החומר ואת היחס בין החומרים והשפעתם בחומר.

זמן בדרך כלל הוא גורם זניח בעקומת המאמץ-מעוות אבל בהעמסה גבוהה/ מאמץ מתיחה גבוה יש השפעה של הזמן ומהירות ההעמסה על הכניעה ועל השבר.

$\mathrm {\sigma _{t}} =K({\dot {\epsilon }}_{T})^{m}$

כאשר m הוא מקדם רגישות העיבור. ככל שm גבוה יותר ההתנגדות ליצירת צוואר גדולה יותר, בדומה למקדם הקיים במנגנון הקשיית המעוותים.

מקדם דומיננטי נוסף היא הטמפרטורה. הטמפרטורה שולטת בהיווצרות נקעים ובדיפוזיה בחומר. ככל שהטמפרטורה עולה עבור חומר פריך, החומר הפריך יתנהג בצורה קרובה יותר להתנהגות חומר משיך.

לקריאה נוספת

קישורים חיצוניים

מדיה וקבצים בנושא עקומת מאמץ-עיבור בוויקישיתוף

הערות שוליים

^ Luebkeman, C., & Peting, D. (2012, 04 28). Stress–strain curves. Retrieved from http://pages.uoregon.edu/struct/courseware/461/461_lectures/461_lecture24/461_lecture24.html.
^ Thomas Courtney, Mechanical behavior of materials, Waveland Press, Inc, 2005, עמ' 6-13
^ Beer, F, Johnston, R, Dewolf, J, & Mazurek, D. (2009). Mechanics of materials. New York: McGraw-Hill companies. P 51.
^ Beer, F, Johnston, R, Dewolf, J, & Mazurek, D. (2009). Mechanics of materials. New York: McGraw-Hill companies. P 58.
^ Mechanical Properties of Materials
^ Beer, F, Johnston, R, Dewolf, J, & Mazurek, D. (2009). Mechanics of materials. New York: McGraw-Hill companies. P 59.

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

28429009עקומת מאמץ-עיבור

[1] Luebkeman, C., & Peting, D. (2012, 04 28). Stress–strain curves. Retrieved from http://pages.uoregon.edu/struct/courseware/461/461_lectures/461_lecture24/461_lecture24.html.

[2] Thomas Courtney, Mechanical behavior of materials, Waveland Press, Inc, 2005, עמ' 6-13

[3] Beer, F, Johnston, R, Dewolf, J, & Mazurek, D. (2009). Mechanics of materials. New York: McGraw-Hill companies. P 51.

[4] Beer, F, Johnston, R, Dewolf, J, & Mazurek, D. (2009). Mechanics of materials. New York: McGraw-Hill companies. P 58.

[5] Mechanical Properties of Materials

[6] Beer, F, Johnston, R, Dewolf, J, & Mazurek, D. (2009). Mechanics of materials. New York: McGraw-Hill companies. P 59.

[1]

[2]

[3]

[4]

[5]

[6]

מאמץ (הנדסה)
מאמצים	מאמץ • מאמץ גזירה • מאמץ כפיפה • מאמץ לחיצה • מאמץ מתיחה • מאמץ פיתול • מאמץ קריסה • עייפות החומר
נושאי עזר	מומנט כפיפה • מומנט כוח • אלסטיות • מעוות • חוק הוק • עקומת מאמץ-עיבור • כניעה (הנדסה)
מודולי האלסטיות	מודול האלסטיות • מודול הגזירה • מקדם פואסון • קבועי לאמה • מודול הנפח
שטחים ונפחים	שטח • מומנט התמד • מומנט ההתמד של השטח • מומנט התמד פולרי של השטח • משפט שטיינר-הויגנס • טנזור התמד • טבלת טנזורי התמד • מומנט ראשון של שטח
נושאים משלימים	חוזק חומרים • טנזור מאמצים • מאמצים ראשיים • מעגל מור • היפותזות חוזק • שיטות אנרגיה • חוקי קסטיליאנו

עקומת מאמץ-עיבור

תוכן עניינים

שלבים

הקשר בין עקומת מאמץ-מעוות הנדסי למאמץ אמיתי

סיווג חומרים

חומרים משיכים

חומרים פריכים

גורמים משפיעים

לקריאה נוספת

קישורים חיצוניים

הערות שוליים

תפריט ניווט

עקומת מאמץ-עיבור

שלבים

הקשר בין עקומת מאמץ-מעוות הנדסי למאמץ אמיתי

סיווג חומרים

חומרים משיכים

חומרים פריכים

גורמים משפיעים

לקריאה נוספת

קישורים חיצוניים

הערות שוליים

תפריט ניווט

חיפוש