כופלי לגראנז'

העקום האדום מתאר את האילוץ g(x, y)=c. העקומים הכחולים הם קווים שווי ערך (קווי גובה) של (f(x, y. הנקודה שבה האילוץ האדום משיק לעקום הכחול היא נקודת מקסימום של (f(x, y לאורך עקומת האילוץ, מכיוון ש-d₁ > d₂.

במתמטיקה, כופלי לגראנז' הם משתנים מלאכותיים המוספים לפונקציה ממשית בת כמה משתנים, על-מנת למצוא נקודות קיצון מקומיות של הפונקציה בכפוף לאילוצים. משתנים אלה קרויים על-שמו של המתמטיקאי ז'וזף לואי לגראנז', ונעשה בהם שימוש נרחב במתמטיקה, בפיזיקה (בפרט במכניקה אנליטית) ובחקר ביצועים לפתרון בעיות תכנון לא-ליניארי.

השיטה הבסיסית למציאת נקודות קיצון של פונקציה גזירה בעלת כמה משתנים, בתחום פתוח, היא להשוות את הנגזרות החלקיות לאפס. אכן, על פי משפט פרמה, הנגזרות החלקיות מתאפסות בכל נקודת קיצון של פונקציה גזירה בתחום פתוח. בתחום שאינו פתוח, עשויות להיות נקודות קיצון גם על השפה. אילוצים על המשתנים, הנתונים בצורת משוואה כגון $\ x^{2}+y^{2}+z^{2}=1$, הופכים את התחום לקבוצה סגורה, שכולה שפה, ובכך מונעים את השימוש הישיר בשיטת הנגזרות החלקיות. שימוש בכופלי לגראנז' הופך בעיה עם אילוצים לבעיה בלי אילוצים, ובכך מאפשר להשתמש בהשוואת הנגזרות לאפס.

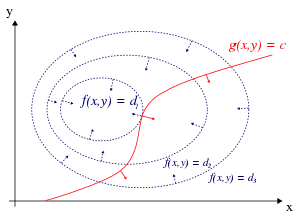
ניתן לתת אינטואיציה גרפית לשיטה בכך שבנקודות מקסימום של הפונקציה בכפוף לאילוץ, כיוון הנגזרת הכללי יהיה באותו כיוון של הנגזרת של האילוץ, ולכן הן יהיו שוות אחת לשנייה עד כדי מכפלה בסקלר.

נכונות השיטה

פורמלית, נכונות השיטה של כופלי לגראנז' מתבססת על המשפט שקובע שבכל נקודה סטציונרית של פונקציה ב-n משתנים בהינתן אילוצים מסוימים (כלומר אקסטרמום של ערך הפונקציה כאשר תנועתנו מוגבלת ליריעה מממד נמוך מ-n), וקטור הגרדיאנט של הפונקציה המקורית באותה נקודה ניתן לביטוי כצירוף ליניארי של וקטורי הגרדיאנט של האילוצים באותה נקודה, עם כופלי לגראנז' כמקדמי הצירוף. במילים אחרות, וקטור הגרדיאנט של הפונקציה המקורית באותה נקודה שייך למרחב הנפרש על ידי גרדיאנטי האילוצים; בפרט, עבור n-1 אילוצים (השקולים לעקומה ב-$\mathbb {R} ^{n}$), קו הגובה של הפונקציה המקורית (הניצב לגרדיאנט שלה) ישיק לעקומת האילוצים.

תיאור השיטה

שיטת כופלי לגראנז' הופכת את הבעיה של מציאת נקודות הקיצון של פונקציה בת $\ n$ משתנים $\ f:D\rightarrow \mathbb {R}$ (כאשר $\ D\subset \mathbb {R} ^{n}$ הוא תחום פתוח), בכפוף ל-$\ k$ אילוצי שוויון מהצורה $\ g_{i}(x_{1},x_{2},...,x_{n})=0$, לבעיה של מציאת נקודות הקיצון של פונקציה בת $\ n+k$ משתנים ללא אילוצים. $\ n$ משתנים הם משתנים של הבעיה המקורית ו- $\ k$ משתנים הם כופלי לגראנז'.

השיטה היא להגדיר פונקציה חדשה:

$\ h(x_{1},x_{2},..,x_{n},\lambda _{1},\lambda _{2},...,\lambda _{k})\equiv f(x_{1},x_{2},..,x_{n})+\lambda _{1}g_{1}(x_{1},x_{2},..,x_{n})+\lambda _{2}g_{2}(x_{1},x_{2},..,x_{n})+...+\lambda _{k}g_{k}(x_{1},x_{2},..,x_{n})$, כאשר $\ \lambda _{i}\in \mathbb {R}$ נקראים כופלי לגראנז'. על מנת למצוא נקודת קיצון, נגזור את הפונקציה לפי כל המשתנים - המקוריים והמוספים - ונקבל $\ n$ משוואות מהסוג $\ {\frac {\partial h(x_{1},x_{2},..,x_{n},\lambda _{1},\lambda _{2},...,\lambda _{k})}{\partial x_{i}}}=0$, בנוסף ל-$\ k$ האילוצים $\ g_{i}(x_{1},x_{2},...,x_{n})=0$. הפתרונות למערכת המשוואות המתקבלות הן הנקודות החשודות כנקודות קיצון, שאותן יש לבדוק פרטנית בדרכים אחרות.

ההסיאן

ההסיאן של מערכת המשוואות, תחת הנחות מסוימות, מזהה אילו נקודות חשודות הן נקודות מינימום או מקסימום, ואילו הן נקודות אוכף בלבד.

דוגמאות

• אנו רוצים למצוא את נקודות הקיצון של הפונקציה $\ f(x,y)=xy$ בכפוף לאילוץ שהנקודות הן על המעגל $\ x^{2}+y^{2}=1$. נגדיר:

$\ h(x,y,\lambda )=xy+\lambda \left(x^{2}+y^{2}-1\right)$

המשוואות שנקבל תהיינה:

$\ {\frac {\partial h(x,y,\lambda )}{\partial x}}=y+\lambda {\frac {\partial \left(x^{2}+y^{2}-1\right)}{\partial x}}=0$

$\ {\frac {\partial h(x,y,\lambda )}{\partial y}}=x+\lambda {\frac {\partial \left(x^{2}+y^{2}-1\right)}{\partial y}}=0$

$\ {\frac {\partial h(x,y,\lambda )}{\partial \lambda }}=x^{2}+y^{2}-1=0$

פתרון המשוואות יתן

$\ y=-2x\lambda$

$\ x=-2y\lambda$

ואז, $\ \lambda =-{\frac {y}{2x}}$ ו $\ x^{2}=y^{2}$ ואז, בעזרת האילוץ נקבל $\ x=\pm {\sqrt {\frac {1}{2}}}$ ו $\ y=\pm {\sqrt {\frac {1}{2}}}$.

• פחית היא גליל בנפח $\ V$. חומר הגלם פרופורציוני ישר לשטח הפנים של הגליל $\ A$, לכן נחפש את הנקודה עבורה שטח הפנים הוא מינימלי. לתיאור הגליל דרושים שני משתנים, רדיוס $\ r$ וגובה $\ h$. את נקודת הקיצון אנו צריכים למצוא עבור הפונקציה $\ A(r,h)=2\pi r^{2}+2\pi rh$, כשהאילוץ הוא $\ V=\pi r^{2}h\Rightarrow V-\pi r^{2}h=0$. המשוואות המתקבלות הן:

$\ {\frac {\partial A(r,h)}{\partial r}}=-\lambda {\frac {\partial {V-\pi r^{2}h}}{\partial r}}$

$\ {\frac {\partial A(r,h)}{\partial h}}=-\lambda {\frac {\partial {V-\pi r^{2}h}}{\partial h}}$

פתרונן נותן:

$\ 4\pi r+2\pi h=\lambda 2\pi rh$

$\ 2\pi r=\lambda \pi r^{2}$

ולפיכך, $\ \lambda ={\frac {2}{r}}$ ו $\ h=2r$. ניעזר באילוץ ונקבל $\ r=\left({\frac {V}{2\pi }}\right)^{\frac {1}{3}}$ ו $\ h=\left({\frac {4V}{\pi }}\right)^{\frac {1}{3}}$.

ראו גם

• תכנון לא-ליניארי
• משפט קרוש-קון-טוקר

קישורים חיצוניים

מדיה וקבצים בנושא כופלי לגראנז' בוויקישיתוף

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

כופלי לגראנז'33655518Q598870