E=mc²


E=mc2 (לעיתים מכונה משוואת איינשטיין) היא משוואה נודעת מתחום הפיזיקה שניסח אלברט איינשטיין. המשוואה קובעת את היחס בין מסה (m) של עצם לבין האנרגיה (E) שלו; אנרגיה שווה למסה כפול מהירות האור (c) בריבוע.
השלכותיה של המשוואה נרחבות מאוד. היא ערערה את עקרונות המכניקה הקלאסית, גרמה לגילוי ההיתוך והביקוע הגרעיני והובילה בסופו של דבר להגיית תורת היחסות הכללית.[1]
המשוואה התפרסמה לציבור הרחב בעיקר משום שהובילה לפיתוח פצצת האטום. כיום היא נחשבת לאחת מן המשוואות החשובות והמפורסמות ביותר מתחום הפיזיקה, ומהווה סמל לתרבות ומדע.[2][3]
משמעות המשוואה
בפיזיקה, הגודל "מסה" הוא גודל שמתאר שתי תכונות: כמה גוף מתנגד לתאוצה וכמה הוא מושך דברים אחרים אליו לפי כוח המשיכה. משמעות הנוסחה היא שככל שגוף צובר יותר אנרגיה, המסה שלו תשתנה בהתאם. לדוגמה, כדי לפרק אטום מימן לפרוטון ואלקטרון נפרדים זה מזה (לא קשורים), צריך להשקיע אנרגיה. לפי הנוסחה, ניתן להסיק שמערכת שמכילה פרוטון ואלקטרון שנפרדים זה מזה היא מסיבית יותר ממערכת שמכילה אטום מימן אחד, זאת על אף שבשתי המערכות יש אותם חלקיקים בדיוק. במקרה הזה, לפי הנוסחה, השינוי במסה יהיה בסדר גודל של קילוגרם, קטן פי 100,000 ממסת האלקטרון – ולכן בחיי היום יום האפקט הזה זניח וקשה מאוד למדידה. עם זאת, במאיצי חלקיקים שבהם חלקיקים נהיים מאוד מהירים ואנרגטיים, העלייה במסה היא מובהקת.
ניתן לתאר זאת גם בכיוון ההפוך: כדי ליצור חומר במסה , צריך להשקיע אנרגיה בסך (דבר שניכר בתופעות כמו יצירת זוגות).
על פי המשוואה, כמות האנרגיה המקסימלית שניתן להפיק מעצם זהה למסת העצם כפול מהירות האור בריבוע. אפילו למסות קטנות יחסית, ערכה של אנרגיית המנוחה גבוה מאוד.[4]
ישימות
את המשוואה E=mc² ניתן להחיל על כל העצמים בעלי מסה, שכן היא קובעת שמסה היא אנרגיה. ישימות הנוסחה לעצמים נעים תלויה בהגדרת המסה בה נעשה שימוש במשוואה.
בפיזיקה המודרנית המסה היא אינווריאנטית (אנ') בעוד שאנרגיה אינה כזו. לכן, בדרך כלל, משוואה זו מיושמת על עצם שאינו נע מנקודת הייחוס של הצופה. מנקודת המבט של נקודת ייחוס אחרת, העצם עשוי להיות בתנועה, ולכן המשוואה אינה ישימה לנקודת ייחוס שנייה זו.
שימוש במסה יחסית
המאמרים המקוריים של איינשטיין התייחסו ל־ במה שנקרא היום "מסה יחסית". דבר זה קשור ל"מסת מנוחה" (כלומר מסת העצם מנקודת היחוס לפיה הוא נייח) בדרך הבאה:
אך כדי להגיע למשוואה עלינו להתחיל במשוואה (זוהי למעשה ה"נורמה" היחסותית של וקטור ה־4־תנע במרחב מינקובסקי), כאשר התנע הוא אפס (ולכן גם המהירות היא אפס). כלומר, במקרה במיוחד שבו העצם נייח, שווה ל־, או . זהו המקרה היחידי בו קיימת המשוואה בצורה . בכל מהירות אחרת, עלינו להחזיר למשוואה את הגורם במשוואה הכללית.
אם נציב כעת במשוואה נקבל , כך שבזמן מנוחה, כלומר במהירות , הכמות של מסת מנוחה שווה לכמות המסה היחסית, וניתן לכתוב את המשוואה כ־: אין הבדל מלבד שייתכן כי נצטרך לומר כי הוא עבור . אזי, תוך שימוש במסה היחסית, המשוואה שבכותרת חייבת להיכתב כ־ ואינה ישימה לעצמים הנעים במהירות כלשהי, אלא רק במהירות אפס, משום ש־ שכאן הוא רק עבור .
המשוואה הכללית ביותר היא
שימוש במסת מנוחה
פיזיקאים מודרניים כמעט שאינם עושים שימוש במסה יחסית, והם נוהגים להשתמש ב־m לציין מסת מנוחה כך ש־E = mc² היא "אנרגיית מנוחה", כלומר האנרגיה של העצם כשהוא במנוחה. במקרה זה המשוואה ישימה רק לעצמים נייחים. הצורה המודרנית של המשוואה עבור עצם בעל מהירות כלשהי היא:
- ,
כאשר הוא התנע היחסותי של העצם. עובדה זו מצמצמת את E = mc² למקרה של מהירות אפס. לצורך הבהירות, למרות צורת השימוש המודרנית, בהמשכו של ערך זה נעשה שימוש ב־m עבור מסה יחסית וב־m0 עבור מסת מנוחה.
קירוב במהירויות הנמוכות מאוד יחסית למהירות האור
מכיוון שאנרגיה המנוחה היא m0c², וסך האנרגיה היא אנרגיה קינטית ועוד אנרגיית המנוחה, אזי האנרגיה הקינטית היחסית מבוטאת על ידי
ובמהירויות הנמוכות מאוד יחסית למהירות האור מתאים ביטוי זה לביטוי הקלאסי של אנרגיה קינטית.
- .
ניתן להראות ש־ על ידי הרחבת תוך שימוש בטורי טיילור.
- .
הצבה מחדש במשוואה המקורית תתן:
- ,
מכאן, שבאנרגיות נמוכות הביטוי הקלאסי לאנרגיה קינטית הוא קירוב של האנרגיה הקינטית היחסותית. אולם תורת היחסות מוסיפה עוד אנרגיה שלא הוגדרה קודם - אנרגיית המנוחה, שיש לגוף מעצם קיום המסה שלו. איינשטיין הראה כבר כי המכניקה הקלאסית שגויה במצבים של מהירויות גבוהות או של כבידה חזקה. אולם עבור המקרים שנדונו בעת פיתוח המכניקה הקלאסית, ושרלוונטיים ברוב המוחלט של חיי היום יום, המכניקה הקלאסית היא קירוב טוב של המכניקה היחסותית.
לידת המשוואה
תרומות קודמות
איינשטיין פרסם את המאמר שבו הודיע על תגליתו בשנת 1905, אך שורשי התגלית נעוצים בהנחות שונות, שמקורן שנים רבות קודם לכן. איינשטיין לא היה היחיד שקשר אנרגיה למסה, אבל היה הראשון שהציג זאת כחלק מתאוריה רחבה ויותר מכך, הסיק את הנוסחה מתוך ההנחות של תאוריה זו.
ניתן לחלק את תיאור פיתוח המשוואה לפי גורמיה:
E – אנרגיה ו - m – מסה
אחת מהנחות הבסיס שעליהן נשענת המשוואה היא, שאנרגיה אינה יכולה להיווצר או להיעלם, אלא רק להחליף צורה – הנחה שמהווה את חוק שימור האנרגיה, הקובע שכמות האנרגיה במערכת סגורה היא קבועה ואינה מסוגלת להיעלם או להיווצר, ואת החוק הראשון של התרמודינמיקה שמרחיב את חוק שימור האנרגיה ומחיל אותו גם על אנרגיה בצורת חום. משום כך, האנרגיה העודפת שתוזרם למערכת לא תוכל להמשיך לתפקד כאנרגיה ולא תוכל להיעלם; היא תיאלץ, בסופו של דבר, להפוך למסה.[5]
בדומה לאנרגיה, הנחת בסיס חשובה נוספת לתיאוריה היא חוק שימור החומר, הקובע שחומר אינו יכול להיווצר או להיעלם בתוך מערכת סגורה, אלא רק לשנות את צורתו. לפני מחקרו של איינשטיין, עמדו שני חוקי השימור הללו בפני עצמם. E=mc² חיברה ביניהם: לא רק שאנרגיה יכולה להפוך לאנרגיה בצורה אחרת וחומר יכול להפוך לחומר בצורה אחרת, אלא שאנרגיה יכולה להפוך לחומר, וחומר יכול להפוך לאנרגיה.[4][6] תגלית זו הפכה את שני חוקי השימור הללו לבלתי מדויקים, ובמקומם נוסח חוק מאוחד שנקרא "חוק שימור האנרגיה-מסה", שקובע כי בכל תהליך שהוא סכום האנרגיות והמסות של הגופים והמערכות המשתתפים בתהליך נשאר קבוע.[7]
c – מהירות האור
הנחת בסיס חשובה נוספת, שביסס איינשטיין בתורת היחסות הפרטית, היא שמהירות האור בריק היא הגבול העליון למהירות שבה יכולים חלקיק או אנרגיה לנוע. לכן, כאשר כמות האנרגיה שמוכנסת למערכת מאיצה את המהירות קרוב למהירות האור, היא אינה יכולה להמשיך בהאצת המהירות, ובהתאם לחוק שימור האנרגיה גם לא תוכל להיעלם, ולכן תהפוך למסה.
– בריבוע
אייזק ניוטון הגדיר את האנרגיה של חומר כלשהו כמכפלה של המסה שלו ומהירותו, כלומר . לדוגמה, אם גוף במשקל 6 קילוגרמים ינוע במהירות של 10 קמ"ש, הוא יאצור 60 יחידות אנרגיה. הפיזיקאי גוטפריד לייבניץ, לעומת זאת, התנגד לדעתו של ניוטון וסבר ש־. אך מסקנותיו היו תאורטיות בלבד והוא לא הצליח להוכיחן.
בתחילת המאה השמונה עשרה חקרה המדענית אמילי די שאטלה, יחד עם הפילוסוף וולטר, את הנוסחאות של ניוטון ולייבניץ. די שאטלה הסכימה עם דעתו של לייבניץ, אך לא יכלה לקבל אותה ללא הוכחות מעשיות. לבסוף מצאה את ההוכחות בניסויים של החוקר ההולנדי וילם סחרווסנדה, שעסקו במדידת נפילה חופשית אל קרקע רכה. הניסויים תמכו באופן חד משמעי במשוואה של לייבניץ; לדוגמה, כאשר הופלו אל משטח רך שני כדורים באותו משקל שאחד מהם נע במהירות גדולה פי שלושה, הכדור שמהירותו גבוהה יותר שקע פי 9 עמוק יותר בקרקע, ולא פי 3.[8]
כך הגיעה די שאטלה למסקנה ש־. משוואה זו היוותה גם היא בסיס חשוב למשוואה של איינשטיין, משום שקבעה שהאנרגיה מתייחסת למהירות בריבוע, אך היא התייחסה לאנרגיה הקינטית בלבד ולא לאנרגיה שאצורה במסת החומר.
פרסום המאמר
ב־27 בספטמבר 1905 שלח איינשטיין לשנתון הפיזיקה מאמר בן כ־30 עמודים בשם "Zur Elektrodynamik bewegter Körper" ("על האלקטרודינמיקה של גופים נעים"), בו שטח את מסקנותיו לגבי תורת היחסות. מספר שבועות לאחר מכן הוא הגיע למסקנה נוספת הנובעת מתורת היחסות, ומיהר לשלוח לעיתון תוספת של שלושה עמודים למאמר, בשם "Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig?" ("האם ההתמדה של גוף תלויה בתכולת האנרגיה שלו?"). בתוספת זו נוסחה לראשונה משוואתו המפורסמת. מאמר זה הוא אחד מהמאמרים הידועים כיום כמאמרי שנת הפלאות שלו.[9]
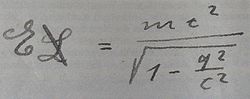
איינשטיין לא ניסח במאמר משוואה זו בדיוק; בסמלים שבהם השתמש איינשטיין המשוואה נראתה כך - (כשהאות L מייצגת אנרגיה במקום E, ו-v מייצגת את מהירות האור).[10] במאמר נכתב: ”אם גוף משחרר אנרגיה L בצורת קרינה, קטנה מסתו ב־L/c².”[11] קרינה היא במקרה זה אנרגיה קינטית, והמסה היא מושג המסה כפי שהיה בשימוש באותה תקופה, מה שקרוי כיום מסת מנוחה או מסה אינווריאנטית. באותה תקופה הייתה קביעה זו השערה תאורטית שלא הוכחה בניסויים.
לאחר שנים העתיק איינשטיין את מאמר היחסות המקורי שלו בכתב ידו, כדי למכור אותו במכירה פומבית. תוך כדי כתיבה הוא שאל את מזכירתו, שהכתיבה לו את המאמר, "זה מה שאמרתי?" היא השיבה בחיוב. "הייתי יכול לומר את זה בצורה הרבה יותר פשוטה", הוא אמר.[12]
קבלה ראשונית
בתחילה התאוריה התקבלה בפקפוק רב, ואף בבוז, בקרב הפיזיקאים. הפיזיקאי זוכה פרס נובל, ארנסט רתרפורד, אמר על הנושא בכנס מדעי בלונדון: ”מי שמדבר על אנרגיה אטומית מדבר שטויות.”[2] כאשר ניסה איינשטיין להתקבל כמרצה באוניברסיטת ברן הוא צירף למכתבו את מאמר היחסות שלו, אך נדחה.[13][14] הפרופסור טירינג מאוניברסיטת וינה אמר כי ”הנשימה נעצרת למחשבה, מה עלול לקרות אם תשתחרר בצורת התפוצצות האנרגיה הרדומה בלבנה אחת ויחידה... אך דבר זה לא יקרה לעולם...”[15]
בשלב זה גם איינשטיין עצמו לא היה בטוח לחלוטין במסקנותיו. הוא הודה בפני ידידו, קונרד הביכט: ”הרעיון משעשע ומרתק, אך אם האל צוחק ממנו ומתלוצץ על חשבוני – זאת איני יכול לדעת.”[16]
הניסוי הראשון שהוכיח לבסוף את התאוריה של איינשטיין התבצע ב־1932. הפיזיקאים ג'ון קוקרופט וארנסט וולטון מאוניברסיטת קיימברידג' הצליחו להאיץ גרעיני מימן, עד שפגעו בגרעינים של ליתיום. בהתנגשות נוצרו שני גרעינים של הליום (חלקיקי α, המכילים שני פרוטונים ושני נייטרונים), אשר נעו במהירות גבוהה בכיוונים הפוכים. סכום המסות של הפרוטון וגרעין הליתיום הוא יותר גדול מן המסה של שני חלקיקי α. המסה שהלכה לאיבוד בתהליך הזה הפכה לאנרגיה הקינטית של שני חלקיקי α. כך אישר ניסוי זה את התופעה של הפיכת מסה לאנרגיה, והוכיח שהמאזן הכמותי בין שתיהן נקבע על ידי הנוסחה E=mc^2.[2]
השלכות
השלכות תאורטיות
ערעור המכניקה הקלאסית
| |
ראו גם – היסטוריה של הפיזיקה |
המשוואה ערערה חלק מהעקרונות שהתקבלו קודם לכן על ידי הקהילה המדעית, כגון אחת ההנחות של המכניקה הקלאסית של ניוטון, לפיה לגוף במנוחה אין אנרגיה. על פי המשוואה של איינשטיין, לעומת זאת, לגוף במנוחה יש אנרגיה – בצורת מסה.[17]
למרות זאת, המכניקה הניוטונית יכולה להתקיים במצבים מסוימים ללא סתירה ל-E=mc². המכניקה הניוטונית התייחסה למצבים פשוטים ויומיומיים, שהתנועה בהם הייתה כה איטית ביחס למהירות האור עד שהיה אפשר להתעלם ממנה. כך הצליחה להסביר היבטים שונים בהנדסה ובפיזיקה, מלבד הנושאים העוסקים בחקר האטומים וגרמי השמיים. לכן, המכניקה הניוטונית ניתנת לשימוש לגבי תופעות מסוימות, אך ההשקפה הכללית שלה מוטעית; ניוטון האמין כי המרחב והזמן הם ישויות פיזיקליות "מוחלטות" - קבועות ויציבות לחלוטין, וקביעה זו הייתה בסיס מרכזי לתאוריות שלו. אך כיום, לאחר תורת היחסות, נחשבים עקרונותיו של ניוטון כמקרה פרטי מתוך מערכת רחבה יותר.[18]
מקור אנרגיית הכוכבים
 ערך מורחב – היתוך גרעיני
ערך מורחב – היתוך גרעיני
לאחר פרסום המשוואה וקבלתה, מדענים רבים ניסו להסביר באמצעותה את מקור האנרגיה של השמש; ההבנה שאנרגיה רבה כל כך עשויה להיות אצורה במסה קטנה כל כך, אפשרה להבין את מקור האנרגיה של השמש ושאר הכוכבים ביקום.[3] אך עד אז הניסויים הוכיחו את יעילות המשוואה בחומרים רדיואקטיביים בלבד, ולא נמצאו שום עקבות של חומרים רדיואקטיביים על השמש. בתחילת המאה ה-20, הדעה הרווחת הייתה שהשמש עשויה מ-66% ברזל טהור. מתכות רדיואקטיביות פולטות אנרגיה בקלות משום שהאטומים שלהם לא יציבים ומתפרקים במהירות. ברזל, לעומת זאת, הוא יסוד יציב במיוחד. אילו השמש הייתה עשויה מברזל היא לא הייתה מסוגלת לפלוט אנרגיה רבה כל כך במשך זמן רב.
בשנת 1925 הצליחה ססיליה פיין לפתור את הבעיה. היא קראה את קווי הספקטרוסקופ בצורה אחרת, והגיעה למסקנה שהשמש מורכבת בעיקר ממימן, ומכילה גם מעט הליום.[19] על פני כדור הארץ אטומי מימן לא נוטים להתפרק באופן טבעי, משום שהם לא נתונים ללחץ גבוה. אך כשהם נמצאים במרכזה של השמש, תחת לחץ גדול, גרעיני המימן עשויים להילחץ ולהיצמד זה לזה עד שבמשך הזמן יתמזגו ויהפכו לאטומי הליום.
מסתו של אטום מימן אחד היא 1 גרם למול. לכן, מסתם של ארבעה אטומי מימן נפרדים היא 4 גרם למול. אך כאשר ארבעה אטומי מימן מתאחדים לאטום הליום אחד, הוא ישקול 3.971 גרם למול. 0.7 האחוזים הנותרים צצים כאנרגיה ונפלטים מהשמש בצורת אור, בדיוק על פי המשוואה.[20] זוהי כמות זעירה, אך השמש גדולה מספיק כדי לספק לכדור הארץ חום ואור. בכל שנייה הופכת השמש 4,000,000 טונות מימן לאנרגיה טהורה.[21] תהליך זה נקרא היתוך גרעיני.[22]
גילוי הביקוע הגרעיני
 ערך מורחב – ביקוע גרעיני
ערך מורחב – ביקוע גרעיני
בשנת 1938 הוביל אוטו האן סדרת ניסויים שבמהלכם הוזרמו נייטרונים מואטים אל תוך חלקיקי אורניום, בציפייה ליצירת יסוד חדש - כבד יותר מן האורניום. אך למרות המשאבים הרבים שהושקעו בניסוי, החוקרים לא הצליחו לזהות חומר חדש. האן גילה שהאורניום למעשה התפרק לבריום, אך הוא לא הבין כיצד הזרמת הנייטרונים גרמה לכך. הוא דיווח על תוצאותיו כך: ”...ככימאים, עלינו לומר שהחלקיקים החדשים אינם מתנהגים כמו רדיום, אלא כמו בריום; כפיזיקאי גרעין, אין אנו יכולים לאמץ מסקנה זו, המנוגדת לכל הניסיון שיש בפיזיקה הגרעינית.”[23]
האן ביקש את עזרתה של הפיזיקאית ליזה מייטנר, ששהתה בשוודיה, והיא נענתה לבקשתו וניסתה לפתור את הבעיה יחד עם אחיינה, הפיזיקאי אוטו פריש. פריש תיאר זאת כך:
למזלנו, דודתי זכרה כיצד מחשבים מסות של גרעינים... וכך חישבה ששני הגרעינים שנוצרו מחלוקתו של גרעין האורניום יהיו קלים יותר מגרעיון האורניום המקורי, ושההפרש יהיה שווה בערך לחמישית ממסתו של פרוטון. כעת, בכל מקום שבו נעלמת מסה נוצרת אנרגיה, על פי משוואתו של איינשטיין E=mc2...
— רוברט פריש, What Little I Remrmber, עמ' 116
לפי חישוביהם, המטען החשמלי של הפרוטונים בתוך הגרעין מנה כ-200 MeV - כמות אנרגיה עצומה. פריש תיאר את ההתרגשות שאחזה בהם: ”מסה של חמישית הפרוטון היתה שווה בדיוק ל-200 MeV. אז זה היה המקור של אותה האנרגיה; הכל התאים!” [24] כאשר הנייטרונים פגעו בגרעיני אורניום, הם החלו להתנודד ולהתארך כמו טיפות נוזל. עיוות הצורה עשוי להוריד את עוצמת הכוח הגרעיני החזק שמלכד את הגרעין, ואז כוח הדחייה החשמלית יכול לפרק את הגרעין וליצור חומר חדש תוך פליטת אנרגיה רבה.[25]
כך התגלה רעיון הביקוע הגרעיני, שהיווה את הבסיס לפיתוחה של פצצת הביקוע הגרעיני מאוחר יותר.[26][27]
פיתוח תורת היחסות הכללית
 ערך מורחב – תורת היחסות הכללית
ערך מורחב – תורת היחסות הכללית
פוטון הוא "חלקיק" של אור, ומשוואת איינשטיין מעניקה לו מסה זעירה. אם כל גוף בעל מסה מושפע מכוח הכבידה, אזי פוטונים אמורים גם הם להיות מושפעים ממנו. אם כוח הכבידה משנה את מסלול הגופים וגורם לסטייה במסלולם כאשר הם עוברים בסמוך לגוף מסיבי, אזי הגוף המסיבי צריך לשנות את מסלולו של פוטון. אם כוח הכבידה גורם לגופים לאבד אנרגיה כאשר הם נמלטים מהשפעתו של גוף מסיבי, אז פוטון צריך לאבד אנרגיה כאשר הוא עוזב גוף מסיבי. תובנות אלה הובילו את איינשטיין להישגו הגדול ביותר: תורת היחסות הכללית, שעוסקת בכוח הכבידה והשפעותיו.[28]
מחקר על חורים שחורים
 ערך מורחב – חור שחור
ערך מורחב – חור שחור
בשנת 1930 הגה סוברהמניאן צ'נדראסקאר תאוריה יוצאת דופן בנוגע לאופן פעולתם של חורים שחורים: על פי E=mc², כוכב גדול ודחוס שיהפוך את מלאי המסה שלו לאנרגיה במשך זמן ארוך מספיק ייאלץ בסופו של דבר לאבד את המסה המרכזית שלו, וליבתו הריקה תהיה נתונה בלחץ עצום. לפי אותה תאוריה, הלחץ, שהוא סוג של אנרגיה, שווה לכמות של מסה. הכבידה של שריד הכוכב תתעצם בשל המסה הזו, אך תפעל כלפי פנים הכוכב והלחץ יגבר עוד יותר. תוספת הלחץ תתנהג שוב כתוספת מסה והכבידה תתעצם עוד ועוד, עד היווצרות חור שחור בעל כוח משיכה עצום.
תאוריה זו תפסה מקום חשוב בתפיסה המודרנית של חורים שחורים, וזיכתה את צ'נדראסקאר בפרס נובל שנים רבות לאחר מכן.[29]
יישומים מעשיים
פצצת האטום

 ערך מורחב – פצצת ביקוע גרעיני
ערך מורחב – פצצת ביקוע גרעיני
המשוואה הייתה הכרחית לפיתוח פצצת האטום, משום שאופן פעולתה של הפצצה מתבסס על תהליך הביקוע הגרעיני.[20][30][31] בנוסף למעורבותו של איינשטיין בפיתוח הרקע התאורטי לבניית הפצצה, שמו נקשר אליה משום שתמך בפיתוחה על ידי ארצות הברית בחתימתו על מכתב איינשטיין-סילארד וכך גרם להטלת הפצצה על הירושימה ונגסאקי, על אף שלא השתתף באופן אישי בפרויקט מנהטן.[32] מעורבותו בפיתוח המעשי של הפצצה הדגישה גם את הקשר המדעי בין E=mc² לפצצת האטום.
איינשטיין עצמו המעיט בחשיבות תרומתו המדעית לפיתוח הפצצה. בשנת 1955 כתב להיסטוריון צרפתי:
נראה שאתה מאמין שאני, מסכן שכמותי, באמצעות גילוי ופרסום הקשר בין מסה לאנרגיה, תרמתי תרומה חשובה... אתה רומז שהייתי צריך... ב-1905, לצפות את פיתוחן האפשרי של פצצות אטום. אך היה זה בלתי אפשרי, משום שהשגת תגובת השרשרת הייתה תלויה בקיומו של מדע אמפירי שלא היה אפשר לצפותו ב-1905...
גם אם ידע כזה היה זמין, היה זה מגוחך לנסות להסתיר את המסקנה הספציפית שעולה מתורת היחסות הפרטית. לאחר שהתקיימה התאוריה, התקיימה גם המסקנה.
— דייוויד בודאניס, E=mc²: סיפורה של התגלית הגדולה בהיסטוריה, עמ' 250
מכשור רפואי
| |
ראו גם – רפואה גרעינית |
בבתי חולים המשוואה משמשת בקביעות במכשירים שונים לאבחון וטיפול רפואי. טיפול רדיותרפיה, למשל, פועל באמצעות כמויות זעירות של חומרים רדיואקטיביים המכוונים אל הגידולים. כשגרעיני החומר הרדיואקטיבי הלא יציבים מתפרקים, נעלמת לכאורה מסה; האנרגיה הנוצרת מכוונת בעוצמה שדי בה להרוס את הגידול.[33]
טכניקת ההדמיה הרפואית טומוגרפיית פליטת פוזיטרונים מתבססת גם היא על התאוריה של איינשטיין. חומר רדיואקטיבי מוזרק לדמם של הנבדקים ומתפרק שם במהירות. עקבות האנרגיה הנובעת מן המסה הנהרסת מתועדים ביוצאם מן הגוף, וכך מתאפשר דימות מדויק של זרימת הדם או ספיגת תרופות בגוף.[33]
יישומים נוספים

המשוואה באה לידי שימוש גם במכשירים יומיומיים שונים. למשל: גלאי עשן סטנדרטי מכיל בדרך כלל כמות קטנה של אמריציום. הגלאי משתמש באנרגיה שהוא שואב מן האמריציום, לפי המשוואה, וכך מייצר במשך שנים קרן טעונה רגישה לעשן.[33]
מדינות רבות משתמשות ברעיון הפקת האנרגיה ממסה (על ידי ביקוע גרעיני) על מנת להפיק אנרגיה חשמלית.[34] בצרפת, לדוגמה, 75% מהאנרגיה החשמלית מגיעים ממקור זה, שידידותי לסביבה יותר מאשר שריפת פחם ומאפשר הפקת אנרגיה רבה ממסה קטנה יחסית.[26]
הנעה גרעינית משמשת גם צוללות גרעיניות, ומספקת למנוע הצוללות אנרגיה מספיקה לשייט ארוך במהירות גבוהה יחסית, מבלי לעלות אל פני המים לעיתים קרובות כדי לספק חמצן למנוע.[35]
השפעה תרבותית
המשוואה נחשבת כיום לאחת הנוסחאות המפורסמות ביותר מתחום הפיזיקה, ומסמלת תרבות ומדע.[2][3][36] היא מזוהה מאוד עם אלברט איינשטיין ומופיעה פעמים רבות יחד עם דמותו. היא מודפסת על בגדים, בפרסומות למוצרים מסחריים, על שטרות ומטבעות,[37] ומדינות רבות הנפיקו בול שעליו דמותו של איינשטיין יחד עם המשוואה.[2]
לקריאה נוספת
- דייוויד בודאניס, E=mc2: סיפורה של התגלית הגדולה בהיסטוריה, הוצאת כתר
- רוברט פ' קריז, המשוואות הגדולות – פריצות דרך במדע מפיתגורס עד הייזנברג, כתר ספרים, 2008, עמ' 161–190
קישורים חיצוניים
- E=mc², באתר אנציקלופדיה בריטניקה (באנגלית)
- יום הולדת מאה שמח ל־E=mc² של אלברט איינשטיין, BBC (באנגלית)
- על האלקטרודינמיקה של גופים נעים - המאמר המקורי (באנגלית)
- האם ההתמדה של גוף תלויה בתכולת האנרגיה שלו? - המאמר המקורי (באנגלית)
- פרופ' חנוך גוטפרוינד, "אודיסיאה", המשוואות הגדולות של הפיזיקה: E=mc2, באתר ynet, 20 באוגוסט 2010
הערות שוליים
- ↑ פריץ רודליך, מפרדוקס למציאות: הרעיונות המרכזיים של הפיזיקה החדשה, עמ' 83
- ^ 2.0 2.1 2.2 2.3 2.4 פרופ' חנוך גוטפרוינד, המשוואות הגדולות של הפיזיקה: E=mc2, באתר ynet
- ^ 3.0 3.1 3.2 אנציקלופדיית אאוריקה
- ^ 4.0 4.1 Michio Kaku, The Theory Behind the Equation, Nova
- ↑ בהקשר זה המסה תתפקד לפי הגדרתה הפשטנית - מידת ההתנגדות לתאוצה. כלומר, הגוף בעל עודף האנרגיה יהיה כבד יותר אך לא גדול יותר.
- ↑ ערן פוס, מהו חוק שימור האנרגיה?, באתר מכון דוידסון
- ↑ יורם קירש, יסודות הפיסיקה, האוניברסיטה הפתוחה, עמ' 61
- ↑ דייוויד בודאניס, E=mc²: סיפורה של התגלית הגדולה בהיסטוריה, עמ' 63
- ↑ איתי נבו, הגאון ששינה את היקום, באתר מכון דוידסון
- ↑ דייוויד בודאניס, E=mc²: סיפורה של התגלית הגדולה בהיסטוריה, עמ' 204
- ↑ ליאור רובננקו, הידעת? המשוואה המפורסמת E=mc² כלל לא מופיעה כלשונה במאמר המקורי שכתב איינשטיין!, באתר מדע גדול, בקטנה
- ↑ Benesh Hoffman, Einstein, Creator and Rebel, עמ' 209
- ↑ המאמר נדחה מכמה סיבות, ביניהן הטיעון שהוא הוגש מודפס, ואילו על פי התקנות יש להגיש תזה בכתב יד.
- ↑ Carl Seeling, Albert Einstein: A Documentary Biography, עמ' 88
- ↑ א. פויירשטיין, יהודים חתני פרס נובל, 1960, עמ' 63
- ↑ Collected Papers of Einstein, Vol. 5, doc 28
- ↑ חיים ברק, מה הקשר בין מסה ואנרגיה? , במדור "שאל את המומחה" באתר של מכון דוידסון לחינוך מדעי, 27 בדצמבר 2009
- ↑ ברנרד כהן, לידתה של פיסיקה חדשה, עמ' 180
- ↑ איתי נבו, החוקרת שהבינה ממה עשויה השמש, במדור "היום לפני במדע" באתר של מכון דוידסון לחינוך מדעי, 10 במאי 2020
- ^ 20.0 20.1 יורם קירש, יסודות הפיסיקה, האוניברסיטה הפתוחה, עמ' 57
- ↑ דייוויד בודאניס, E=mc²: סיפורה של התגלית הגדולה בהיסטוריה, עמ' 158
- ↑ אבי סאייג, האם פצצת מימן חזקה יותר מפצצת אטום, ומדוע? רון, במדור "שאל את המומחה" באתר של מכון דוידסון לחינוך מדעי, 16 באפריל 2012
- ↑ פוליטיקה, כימיה וגילוי הביקוע הגרעיני, באתר מט"ח
- ↑ דייוויד בודאניס, E=mc^2: סיפורה של התגלית הגדולה בהיסטוריה, עמ' 99
- ↑ פיטר אטקינס ולורטה ג'ונס, כרך ב, כימיה כללית, עמ' 463
- ^ 26.0 26.1 גלי וינרב, בלי איינשטיין לא היה וויז: 140 שנה להולדת המדען, באתר גלובס
- ↑ איתי נבו, האיש ששינה את היקום: 60 שנה למותו של אלברט איינשטיין, באתר הידען
- ↑ דוגמאות להמרת מסה-אנרגיה, באתר פרחי מדע
- ↑ דייוויד בודאניס, E=mc²: סיפורה של התגלית הגדולה בהיסטוריה, עמ' 172
- ↑ ז'אן-ברנאר פואי, אנשים גדולים, התחלות קטנות, עמ' 19
- ↑ אורי פז, איינשטיין והנשק הגרעיני, באתר פאזל, 4 באוגוסט 2005
- ↑ Erin Blakemore, How a Refrigerator Led to Einstein’s Pleas for Atomic Bomb Research, National Geographic
- ^ 33.0 33.1 33.2 דייוויד בודאניס, E=mc^2: סיפורה של התגלית הגדולה בהיסטוריה, עמ' 167
- ↑ פיטר אטקינס ולורטה ג'ונס, כרך ב, כימיה כללית, עמ' 462
- ↑ עזרא להד, צוללות אטומיות ואפשרויות הפעלתן, ביטאון חיל הים, עמ' 8
- ↑ Hans Arora, EINSTEIN'S THEORY OF RELATIVITY: IMPLICATIONS BEYOND SCIENCE?, Helix
- ↑ מטבע ישראלי עם דמותו של אלברט איינשטיין ו-E=mc², באתר החברה הישראלית למדליות ולמטבעות
E=mc²33797788Q35875































