תורת הקשרים

קשר התלתן, הקשר הלא-טריוויאלי הפשוט ביותר

הדמיה תלת-ממדית של קשר התלתן

תורת הקשרים היא תורה טופולוגית, החוקרת את ההיבטים המתמטיים של קשרים, של מבנים דומים להם (כמו שזרים וצמות), ושל הכללות מתמטיות שלהם. מלבד היישומים שלה במתמטיקה עצמה, יש לתורה זו יישומים גם בכימיה, בפיזיקה ובתחומים נוספים, כגון חישוב קוונטי.

עיסוק מרכזי של תורת הקשרים הוא לענות על השאלה מתי שני קשרים נתונים הם זהים זה לזה.

קשרים, דיאגרמות ושזרים

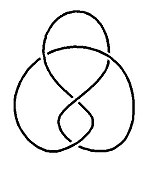
קשר השמונה	דיאגרמה של קשר השמונה

הקשרים המתמטיים שתורת הקשרים חוקרת הם מודלים מתמטיים לקשרים שאנו פוגשים בחיי היום-יום: כאלו שאפשר ליצור בנקל מחבל או משרוך. הקשרים האלה מצויים במרחב התלת-ממדי, והמטרה היא לחקור את המאפיינים שלהם שאינם משתנים תחת עיוות רציף במרחב העוטף אותם. כדי לתאר קשרים בצורה נוחה וחד-משמעית, מציירים דיאגרמה של הקשר, שהיא התמונה הדו-ממדית שרואים כשמתבוננים בקשר מלמעלה. המוסכמה היא לבחור נקודת מבט שממנה לכל היותר שני מקטעים של החבל חוצים זה את זה באותה נקודה, ולהציג את נקודות החצייה - הקרויות "צמתים" (crossings) - כאשר המקטע העליון שלם, והתחתון מחוק מעט (ראו דוגמה משמאל).

דיאגרמה של סמל הטבעות של בית בורומאו

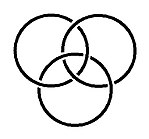
קשר, על-פי ההגדרה, הוא מסילה סגורה העשויה להיות מפותלת במידה רבה או מועטה (ראו הגדרה להלן). מבנה הכולל כמה קשרים, שזורים זה בזה, קרוי שזר (ובאנגלית link). שתי טבעות המונחות זו לצד זו הן שזר. אם הטבעות עוטפות זו את זו, זהו שזר אחר. דוגמה מפורסמת אחרת היא הטבעות הבורומאניות, שדיאגרמה שלהן מופיעה משמאל.

היסטוריה

הקשר הפשוט ביותר הוא בעל צורת טבעת, שאותה אפשר לתאר במישור ללא צמתים כלל. הקשר הזה נקרא "אל-קשר" (ובאנגלית the unknot) או "הקשר הטריוויאלי". קשרים שיש להם רק צומת אחד או שניים אפשר להתיר בקלות. הדיאגרמה של כל קשר אמיתי כוללת לפחות שלושה צמתים.

הראשון שזיהה שקשרים ניתנים לחקירה מנקודת מבט מתמטית היה קרל פרידריך גאוס, אשר ב-1794 המציא שיטת סימון מיוחדת לקשרים המקודדת בתוכה את התכונות של קשר נתון (קוד גאוס). מאוחר יותר בחייו גאוס נתקל בתורת הקשרים בשלושה הקשרים שונים: ב-1804 בהקשר של חקירותיו באסטרונומיה, בהקשר של חקירותיו בגאומטריה, וב-1833 בהקשר של עבודתו בפיזיקה בתורת האלקטרומגנטיות. הצורך להגדיר את התחום עלה בתודעתו של גאוס לראשונה כאשר ניסה לקבוע את התחום השמיימי (חלקה של הספירה השמיימית) שבו שביטים ואסטרואידים עשויים להופיע, תחום אותו הוא מכנה Zodiacus, וכך התעוררה בעיה טופולוגית במחקר אסטרונומי בפעם הראשונה (נכלאס, כרך 6, מאמר "Grenzen der geocentrischen orter der planeten" בעמודים 106 - 121). תוצאות מאוחרות יותר עסקו בתורת הצמות, בסובכים (Tangles) ובשזרים. הנכלאס של גאוס מכיל איורים מעוררי דמיון של צמות, וההערות המופיעות בו מעידות כי גאוס היה הראשון לחקור את המבנה הטופולוגי של צמות וייתכן שאף לחשוב על חבורת הצמות. גאוס גם מצא במאמר קצר מ-1844 את כל הקשרים שהדיאגרמה שלהם מכילה לכל היותר ארבעה צמתים. ב-1833, בהקשר של בעיה אלקטרומגנטית מסוימת, הוא הגדיר את מספר הקישור (linking number) ופיתח שיטה לחשבו באמצעות אינטגרל כפול מתאים (Gauss's linking integral). רעיונותיו של גאוס הכתיבו את אווירת המחקר בגטינגן של אותה תקופה, והספר הראשון שעסק באופן מוצהר בטופולוגיה, ספרו של תלמידו יוהאן בנדיקט ליסטינג, הוקדש לגאוס.

את החקירה השיטתית של קשרים החל פטר טייט (Peter Tait, 1831-1901), שעסק במיון של קשרים על-פי הדיאגרמות שלהם (ראו להלן). הוא הגדיר את "מספר הצמתים" של קשר כמספר הצמתים הקטן ביותר בדיאגרמה של הקשר, ויצר רשימה מפורטת של כל הקשרים שמספר הצמתים שלהם אינו עולה על 7. אחר-כך נעזר טייט בתומאס קירקמן (Thomas Kirkman) כדי להרחיב את הרשימה עד ל-9 צמתים.

הגישה השלטת באותו זמן הייתה שכדי להבדיל בין קשרים, די "לראות" שהם שונים זה מזה, ושאי-אפשר לפתל אחד מהם עד שיתקבל הקשר האחר בלי לקרוע את החבל. מאוחר יותר, עם התבססותה של הטופולוגיה כתחום מתמטי מאורגן, היה ברור שאין בכך די. יש למצוא דרכים להוכיח ששני קשרים נבדלים זה מזה. כך נוצרה הבעיה היסודית של תורת הקשרים: למצוא אלגוריתם שיקבע האם שני קשרים נתונים זהים זה לזה, אם לאו. הגישה המתמטית הכללית לבעיות כאלה היא לאתר אינווריאנטים, גדלים שאפשר לחשב מתוך הקשר, ושיהיו שונים זה מזה עבור קשרים שונים, לפחות בחלק מהמקרים.

דוגמה לאינווריאנט כזה הוא מספר הצמתים: אם קשר אחד ניתן להצגה בדיאגרמה עם 8 צמתים וקשר אחר דורש 10 צמתים לפחות, הם חייבים להיות שונים זה מזה. הבעיה היא שקשה לחשב את מספר הצמתים. אכן, רק בראשית המאה העשרים נמצאה הדרך להראות שקיימים בכלל קשרים שאינם שקולים לאל-קשר!

ב-1976 תיאר Waldhansen אלגוריתם המאפשר להבדיל בין כל שני קשרים; האלגוריתם מבוסס על רעיונות של Haken מ-1954 ו-1961.

סכום קשיר וקשרים ראשוניים

אחת הבניות היסודיות בתורת הקשרים היא הסכום הקשיר של שני קשרים נתונים. כדי לחבר שני קשרים, מנתקים כל אחד מהם בנקודה אחת, ומחברים את הקצוות זה לזה כבאיור משמאל. הקשר המתקבל איננו תלוי בנקודות שבהן בוחרים לנתק את הקשרים המקוריים. את הסכום הקשיר של הקשרים $\ K_{1}$ ו- $\ K_{2}$ מסמנים ב-$\ K_{1}\#K_{2}$.

סכום קשיר של שני עותקים של קשר התלתן

קשר שלא ניתן להציג אותו כסכום קשיר אלא אם אחד המרכיבים הוא האל-קשר, נקרא קשר ראשוני. לקשרים הראשוניים תפקיד דומה לזה של המספרים הראשוניים באריתמטיקה של מספרים טבעיים: משפט שוברט (1949) קובע שכל קשר אפשר להציג באופן יחיד (עד כדי סדר) כסכום קשיר של מספר קשרים ראשוניים.

דיאגרמה נקראת דיאגרמה מתחלפת, אם בטיול לאורך המסילה אנו עוברים לסירוגין פעם מעל ופעם מתחת למקטע השני בצומת. קשר שאפשר להציג אותו באופן כזה נקרא קשר מתחלף. דיאגרמה מתחלפת נותנת הצגה 'הדוקה' של הקשר, ולעיתים קרובות הצגה כזו היא בעלת מספר צמתים מינימלי. לכן קל יותר למיין את הקשרים המתחלפים, והיום ידועות טבלאות של כל הקשרים הראשוניים המתחלפים שמספר הצמתים שלהם אינו עולה על 16 (יש כמעט 2,000,000 כאלה).

הגדרה פורמלית

ההבנה האינטואיטיבית מזהה קשר עם מסילה רציפה סגורה במרחב התלת-ממדי (פורמלית - עותק של הספירה החד-ממדית $\ S^{1}$). המעגל הפשוט נבדל מן הקשר המורכב בדרך שבה הוא משוכן במרחב; אם אפשר לעוות את המרחב (באופן רציף, ללא חיתוך או הדבקה) באופן שמעביר קשר אחד לשני, אז הם שקולים זה לזה. שינוי כזה נקרא איזוטופיה.

הגדרה זו פגומה, משום שאם אין מגבילים את "עובי" החבל, אפשר לכווץ כל קשר לנקודה, וכך להפוך כל מסילה סגורה לאל-קשר. כדי למנוע ניוון כזה של התאוריה, מתבוננים בסביבה צינורית שלו (באנגלית: tubular neighborhood), שהיא טורוס מלא אשר כל דיסק מרידיאני בו הומוטופי לדיסק החותך את הקשר בדיוק פעם אחת. לכל קשר אפשר סביבה צינורית על ידי "עיבוי" מספיק חלש, כדי שהטורוס הנוצר לא יחתוך את עצמו. הסביבה הצינורית מאפשרת להגדיר שני קשרים הם שקולים אם קיימת ביניהם "איזוטופיה סביבתית" (באנגלית: Ambient Isotopy), כלומר, הומוטופיה בין סביבה צינורית של הקשר הראשון לסביבה צינורית של הקשר השני.

כדי להימנע מקשרים פתולוגיים, אפשר להגדיר קשר גם כמסילה סגורה ליניארית-למקוטעין (כלומר, המורכבת ממספר סופי של קטעים ישרים). תחת הגדרה זו, אומרים ששני קשרים שקולים זה לזה, אם אפשר לעבור מאחד לשני במספר סופי של צעדים, שבכל אחד מהם מחליפים צלע אחת של משולש בשתיים האחרות, או להפך, ובלבד שהמשולש אינו נוגע באף צלע אחרת של הקשר.

צעדי ריידמייסטר

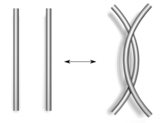
הצעד הראשון: פרימת לולאה עודפת	הצעד השני: התרת זוג צמתים	הצעד השלישי: הסעת לולאה מעל או מתחת צומת
צעדי ריידמייסטר

הגדרת הקשר כמסילה סגורה המורכבת מקטעים ישרים, מאפשרת להוכיח משפט חשוב של ריידמייסטר, הקובע שבין שתי דיאגרמות של אותו קשר אפשר תמיד לעבור במספר סופי של צעדי ריידמייסטר. יש שלושה צעדי ריידמייסטר חוקיים (ראו איור), וקל לראות ששלושתם אינם משנים את הקשר שאותו הדיאגרמה מתארת. לכל קשר K, מספר צעדי ריידמייסטר הדרוש למעבר בין שתי דיאגרמות של K עם n צמתים חסום על ידי פולינום ב-n, ועוללה לפחות כמו n^2.

אינווריאנטים של קשרים

ערך מורחב – אינווריאנטים של קשרים

קשר השמונה, מכוון (באחת משתי דרכים אפשריות)

הבעיה היסודית של תורת הקשרים היא להוכיח ששני קשרים (הנתונים למשל על ידי דיאגרמות) שונים זה מזה. אותה שאלה אפשר לשאול על שזרים באופן כללי, מחד, או על ההפרדה בין קשר נתון לאל-קשר. כדי למלא את המשימה הזו, יש לאתר גדלים שיהיו תלויים בקשר או בשזר, ולא בדיאגרמה המסוימת שנבחרה לייצג אותם; מסיבות שונות, רצוי שהגדלים האלו יהיו ניתנים לחישוב מתוך דיאגרמה. תורת הקשרים משמשת שדה ניסויים לטכניקות שונות בטופולוגיה ובתחומים אחרים של המתמטיקה, והיא מכירה אינווריאנטים רבים ומגוונים. מהם אינווריאנטים מספריים, כמו מספר מרכיבי הקשירות, מספר הקישור הסופר את מספר הפיתולים של המסילה סביב עצמה, הגנוס של משטח סייפרט העוטף את הקשר, מספר הצביעות של הדיאגרמה; ואינווריאנטיים אלגבריים כמו פולינום אלכסנדר או פולינומים נוספים, והחבורה היסודית של המשלים לקשר.

המשלים של הקשר

ב-1905 הציע Wirtinger לחשב, עבור קשר נתון K, את החבורה היסודית $\ \pi _{1}(S^{3}-K)$ של המשלים ב-$\ S^{3}$. זהו אינווריאנט טופולוגי טבעי ומוכר, שהיה לו חלק חשוב בהתפתחות של הטופולוגיה האלגברית. לחבורה היסודית של כל קשר אותה אבליניזציה - $\ \mathbb {Z}$. לפי הלמה של דן (מקס דן, 1910), החבורה היסודית איזומורפית ל- $\ \mathbb {Z}$ אם ורק אם K הוא האל-קשר. ההוכחה שפורסמה לא הייתה שלמה, ותוקנה רק ב-1957. החבורה היסודית תלויה כמובן רק במחלקת ההומיאומורפיזם של המרחב $\ S^{3}-K$. ב-1989 הוכיחו Cameron Gordon ו-John Luecke שאם המשלימים של שני קשרים (אבל לא שזרים!) הומיאומורפיים, אז עד כדי תמונת מראה הקשרים הומוטופיים זה לזה.

עוד ב-1970 הוכיח Bill Turston שכל קשר שייך לאחת משלוש מחלקות: או שהוא ניתן לציור על הטורוס, או שהוא "קשר לווין" (המתקבל מקשירה של קשר בתוך קשר), או שהמשלים שלו הוא יריעה היפרבולית. יתרה מזו, במקרה האחרון הוכיח ג'ורג' מוסטוב שליריעה יש מבנה היפרבולי יחיד בעל נפח סופי, כך שהנפח של המשלים הוא אינווריאנט של קשרים היפרבוליים. Thurston ו-Troels Jorgensen הוכיחו שיכולים להיות רק מספר סופי של משלימי שזרים היפרבוליים בעלי אותו נפח (אם כי יכולים להיות אינסוף שזרים בעלי אותו משלים). קבוצת הנפחים של משלימי שזרים היפרבוליים סדורה היטב.

סכום קשיר של שני עותקים של קשר התלתן הימני; התוצאה סימטרית ביחס לסיבוב במאה ושמונים מעלות	סכום קשיר של קשר תלתן ימני וקשר תלתן שמאלי; סכום זה אינו סימטרי ביחס לסיבוב
קשרים שונים עם אותה חבורה יסודית

עם זאת, החבורה היסודית אינה אינווריאנט אוניברסלי של טיפוס ההומיאומורפיזם של המשלים, ואפילו אינה מאפיינת את הקשר עצמו. לשני הקשרים משמאל (שכבר ראינו שאינם הומוטופיים כי יש להם מספרים שונים של 3-צביעות), יש אותה חבורה יסודית.

אפשר לחשב הצגה של החבורה היסודית באופן הבא. נתונה דיאגרמה מכוונת של הקשר K. מתאימים יוצר לכל קשת בדיאגרמה. כל נקודת מפגש בין קשתות מתאימה ליחס: בנקודת המפגש תמיד שותפות שלוש קשתות: i עוברת מעל j ההופכת ל-k. מתבוננים בנקודת המפגש כאילו i ו-j מגיעות מלמטה, ואז מתקיים היחס $\ x_{j}x_{i}=x_{i}x_{k}$ אם קשת i מגיעה משמאל, ו-$\ x_{i}x_{j}=x_{k}x_{i}$ אם היא מגיעה מימין. לדוגמה, החבורה היסודית של קשר השמונה (עם הדיאגרמה המופיעה משמאל, כאשר המספור מתחיל מן הקשת העליונה) היא $\ \langle x_{1},x_{2},x_{3},x_{4}|x_{1}x_{3}=x_{3}x_{2},x_{2}x_{4}=x_{1}x_{2},x_{4}x_{2}=x_{3}x_{4},x_{3}x_{1}=x_{1}x_{4}\rangle$.

הכללות

קשרים מתוארים כמסילות במרחב התלת-ממדי. לממד המרחב יש כאן תפקיד מכריע: במרחב הארבעה-ממדי אפשר לעוות כל קשר לכל קשר אחר, כך שתורת הקשרים במרחב זה ריקה מתוכן. הכללה בכיוון אחר משנה את המרחב שבו משכנים את הקשר, תוך שמירה על הממד. ממילא הקשר הוא קבוצה קומפקטית, ולכן השיכון במרחב האוקלידי הוא למעשה שיכון בספירת רימן $\ S^{3}$.

באותו אופן אפשר ללמוד גם קשרים המשוכנים במרחבים תלת-ממדיים אחרים, ובמיוחד בכאלו שהגנוס שלהם אינו אפס, כמו הטורוס הסולידי. הכללה מרחיקת לכת יותר עוסקת בשיכון של יריעות מממד גבוה יותר, במקום בשיכונים של הלולאה $\ S^{1}$.

ראו גם

• הומוטופיה
• אינווריאנטים של קשרים

קישורים חיצוניים

1. מספרי קשר של שזרים מתוך חוק אמפר ונוסחת ביו-סבאר; מתוך הבלוג רשימות בפיזיקה עיונית.

• תורת הקשרים, באתר MathWorld (באנגלית)
• תורת הקשרים, באתר אנציקלופדיה בריטניקה (באנגלית)

הערות שוליים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

29517443תורת הקשרים