וקטור נורמלי
קפיצה לניווט
קפיצה לחיפוש
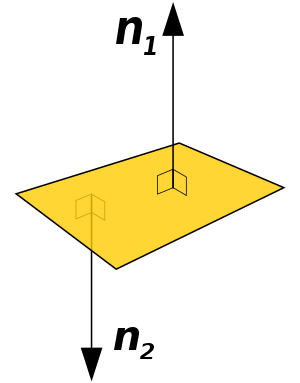
וקטור נורמלי (Normal), המוכר גם בגאומטריה כנורמל, הוא וקטור (או ישר) המאונך לאובייקט המתאים; ישר, מישור או משטח כללי.
מציאת וקטור הנורמל
- מציאת וקטור הנורמל במישור: - כאן וקטור הנורמל הוא: הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle (A,B)} . כלומר, ווקטור הנורמל הוא המקדמים של x ו-y.
- מציאת וקטור הנורמל במרחב: הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ax+By+Cz+D=0} - כאן וקטור הנורמל הוא הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle (A,B,C)} .
- אם הישר או המישור נתונים בהצגה פרמטרית, ניתן למצוא את הווקטור על ידי המשוואות שמראות שהמכפלה הסקלרית של הווקטור הנורמלי בוקטורי הכיוון של הישר או המישור שווה לאפס.
- בהינתן הצגה פרמטרית של משטח כלשהו(לא בהכרח מישור), הווקטור הנורמלי של המשטח יהיה מכפלה וקטורית בין וקטורי הנגזרות החלקיות של הפרמטרים המגדירים של המשטח.
דוגמאות
- מציאת וקטור נורמלי למשטח הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=4-x^2-y^2} בנקודה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle (x,y,z)} . הצגתו הפרמטרית של המשטח היא : הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle S = (x,y,4-x^2-y^2)} , מכיוון שהמשטח דו־ממדי הוא מתואר באמצעות שני פרמטרים בלבד, הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} ו הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} . הנגזרת החלקית של S לפי הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} היא הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\partial S \over\partial x} = (1,0,-2x)} והנגזרת החלקית של S לפי הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} היא . הווקטור הנורמלי למשטח מתקבל על ידי הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\partial S \over\partial x} \times {\partial S \over\partial y} = \begin{vmatrix} i & j &k \\ 1 & 0 & -2x \\ 0 & 1 & -2y\end{vmatrix} = (2x,2y,1)} . כלומר לכל נקודה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle (x,y,z)} , הווקטור הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{n}= (2x,2y,1)} ניצב למשטח הפונקציה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=4-x^2-y^2} . ווקטור היחידה המנורמל הוא הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \widehat{n}= {\vec{n}\over\lVert \vec{n} \rVert} = {(2x,2y,1)\over \sqrt{4x^2+4y^2+1} }} .
שימושים
לווקטור הנורמל מספר שימושים:
- וקטורים מאונכים אם ורק אם המכפלה הסקלרית של הנורמלים שלהם שווה לאפס.
- מגדירים אלמנט שטח אינפיניטסימלי בנקודה P על ידי הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{dA} = (dA)\vec{n}} כאשר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{n}} הוא וקטור נורמל באורך יחידה הניצב למשטח האינפיניטסימלי בנקודה P.
ראו גם
וקטור נורמלי39494214Q273176