מוליכות-על

מוליך-על המרחף מעל מגנט כתוצאה מאפקט מייסנר, שבו קווי שדה מגנטי נדחים מפני מוליך-על.

מוליכות־על (לעיתים נקראת גם על־מוליכות) היא פאזה (מצב) של חומר בפיזיקה של חומר מעובה, בו מתקיימות תכונות של התנגדות חשמלית אפסית ודיאמגנטיות (התנגדות לחדירת שדה מגנטי חיצוני) מושלמת. תכונה זו מתקיימת בחומרים מסוימים בטמפרטורות נמוכות, שדה מגנטי חיצוני חלש וזרם חשמלי חלש בחומר. מאז גילוייה של תופעת מוליכות-העל על ידי האיקה קמרלינג אונס, נתונה תופעה זו במחקר מתמיד, ועודנה מרתקת אנשי מדע וטכנולוגיה גם יחד. בפרט, תופעת מוליכות-העל בטמפרטורות גבוהות יחסית איננה מוסברת בצורה המקובלת על כלל הקהילה המדעית עד היום ופתרונה יהיה, ככל הנראה, פריצת דרך בפיזיקה של חומר מעובה.

היסטוריה

תופעת מוליכות-העל התגלתה בשנת 1911 על ידי האיקה קמרלינג אונס (שאף טבע את המונח) בעת שחקר את ההתנגדות החשמלית של כספית בטמפרטורות נמוכות בעזרת הליום נוזלי (שהתגלה רק זמן קצר קודם לכן). אונס הבחין כי ההתנגדות החשמלית של הכספית יורדת בצורה חריפה ואף מתאפסת עם קירור המערכת לטמפרטורה של 4.2 קלווין. בעשורים שלאחר מכן, התגלו תכונות מוליכות-על אף בחומרים אחרים.

בשנת 1933 גילו וולטר מייסנר (Walther Meissner) ורוברט אוכסנפלד (Robert Ochsenfeld) כי מוליכי-על דוחים שדות מגנטיים חיצוניים, תופעה הנקראת כיום "אפקט מייסנר". האחים היינץ ופריץ לונדון הראו בשנת 1935 כי אפקט מייסנר הוא תולדה של הדרישה לאנרגיה חופשית מזערית בעקבות זרם בחומר המוליך-על. תיאור פנומנולוגי רחב יותר ניתן על ידי גינצבורג ולנדאו בשנת 1950. תאוריית גינצבורג-לנדאו תיארה היטב את התכונות המקרוסקופיות של מוליכי-העל שהיו ידועים באותה התקופה. יתר על כן, אלכסיי אבריקוסוב הראה כי על סמך תאוריה זו צריכים על המוליכים להתחלק לשני סוגים, שיקראו לימים "סוג ראשון" ו"סוג שני". גינצבורג ואבריקוסוב זכו על תגליות אלו בפרס נובל לפיזיקה לשנת 2003 (לנדאו זכה בפרס נובל שנים קודם, בשנת 1962, על תרומותיו לחקר תופעת נוזליות-העל, ובעת מתן הפרס כבר לא היה בין החיים).

תגלית חשובה נוספת התרחשה אף היא בשנת 1950, כאשר עמנואל מקסוול ובמקביל קבוצתם של ריינולדס, סרין, רייט ונסביט גילו כי הטמפרטורה הקריטית של איזוטופים שונים של אותו החומר שונה. תגלית זו הייתה צעד חשוב לקראת הופעתה של תורה מיקרוסקופית המתארת מוליכי-על בשנת 1957 על ידי ברדין, קופר ושריפר. תורה זו, הנקראת על שם ראשי התיבות של מגליה "תורת BCS", הציגה את תופעת מוליכות-העל כתוצאה של אינטראקציה מיקרוסקופית בין האלקטרונים בחומר לבין הפונונים שבגביש, וזיכתה את מחבריה בפרס נובל לפיזיקה לשנת 1972. בשנת 1958 הראה ניקולאי בוגוליובוב כי ניתן לקבל את פונקציית הגל האופיינית של התורה, אשר התקבלה על סמך וריאציה, על ידי שימוש בטרנספורמציה קאנונית על ההמילטוניאן. כמו כן, בשנת 1959 הראה לב גורקוב כי תורת BCS מזדהה עם תורת גינצבורג לנדאו בגבול בו הטמפרטורה קרובה לטמפרטורה הקריטית.

בשנת 1962 פותח הכבל מוליך-העל הראשון, העשוי סגסוגת ניוביום-טיטניום, על ידי חוקרים מוסטינגהאוס. פיתוחו של כבל זה הוביל ליצירת המגנטים הראשונים המבוססים על מוליכות-על. באותה שנה, גילה התאורטיקאי בריאן דייוויד ג'וזפסון כי זרם מוליך-על יכול לזרום בין שני על מוליכים המופרדים ביניהם במבודד. תופעה זו, הנקראת כיום "אפקט ג'וזפסון", מנוצלת ליצירת רכיבים אלקטרוניים, ביניהם ליצירת מגנטומטרים רגישים (בעזרתם ניתן ללמוד את הקוונט של שטף מגנטי $\Phi _{0}={\frac {h}{2e}}$ ובשילוב עם מדידות של אפקט הול הקוונטי למדוד את קבוע פלאנק בצורה המדויקת ביותר כיום). על עבודתו זכה ג'וזפסון בפרס נובל בפיזיקה לשנת 1973.

בשנת 1986, גילו יוהנס גאורג בדנורץ וקרל אלכסנדר מילר, חוקרים של חברת יבמ, תרכובת מבוססת לנתן לה תכונות מוליכות-על עם טמפרטורה קריטית של 35 קלווין, שהיא מעל לערך התאורטי העליון שהיה מקובל באותה התקופה לטמפרטורה קריטית של מוליכי על, שהוא 30 קלווין. תגלית זו זיכתה את מגליה בפרס נובל בפיזיקה בשנה העוקבת. זמן קצר לאחר מכן, גילה צ'ינג וו-צ'ו שתרכובת דומה בה מוחלף הלנטנום באיטריום, חומר המכונה YBCO, היא בעלת טמפרטורה קריטית של 92 קלווין. תגלית זו עוררה עניין רב בין היתר משום שטמפרטורה זו גבוהה מטמפרטורת הרתיחה של החנקן, ולכן ניתן להגיע אליה על ידי קירור בעזרת חנקן נוזלי שהוא יחסית זול ופשוט לשימוש וייצור. מאז התגלו מוליכי-על נוספים בטמפרטורות גבוהות, אך טרם נמצא הסבר תאורטי המקובל בקהילה המדעית למנגנון היוצר את מוליכות-העל בטמפרטורות אלו.

תיאור התופעה

התנגדות חשמלית אפסית

בחומרים רגילים, תלויה ההתנגדות החשמלית בטמפרטורה בקשר הדוק: עם ירידת הטמפרטורה יורדת ההתנגדות החשמלית. באופן כללי, ניתן להסביר תופעה זו על ידי מודל מיקרוסקופי קלאסי ופשטני שלפיו ככל שהטמפרטורה גבוהה יותר, כך מקבלים אטומי החומר יותר אנרגיה קינטית בדמות חום ולכן יכולים להתנגש ביתר קלות עם האלקטרונים בגביש.

בצורה מדויקת יותר, תוך התייחסות לתורת הקוונטים, משפט בלוך קובע כי פונקציית הגל של אלקטרונים בגביש סדור היא מחזורית ולכן בגביש מושלם בטמפרטורה אפסית תיתכן הולכה מושלמת, משום שגל האלקטרון "יחלוף" בצורה מחזורית על פני הגביש. הטמפרטורה גורמת לכך שאטומי החומר מקבלים אנרגיה קינטית ואינם נמצאים בדיוק בנקודות הסריג, אלא מתנודדים סביב נקודת שיווי משקל כלשהי, וגורמים לדעיכות מקומיות של פונקציית הגל של האלקטרון, כך שנדרשת השקעת אנרגיה על מנת לאפשר לאלקטרונים לעבור את הגביש. ככל שיורדת הטמפרטורה, כך יורדת האנרגיה הקינטית של אטומי החומר והם מתקרבים יותר ויותר לנקודת שיווי המשקל. עם זאת, גם בטמפרטורה אפסית, במוליך קלאסי, לא תתאפס ההתנגדות, הן משום שבגביש יש פגמים הגורעים ממחזוריותו המושלמת והן משום שישנן פלקטואציות קוונטיות במיקום האטומים.

עם זאת, ישנם חומרים מיוחדים הנקראים "מוליכי-על" בהם, לפי התאוריות המקובלות, החל מטמפרטורה מסוימת ומטה, עבור שדות מגנטיים מתחת לעוצמה מסוימת ועבור זרמים חשמליים מתחת לסף מסוים, מתאפסת לחלוטין ההתנגדות החשמלית. תכונה זו אושרה פעמים רבות בניסוי, עד לטווח המדידות האפשרי (ניסיונית, ייתכן כי חומרים אלו הם בעלי התנגדות חשמלית שהיא מתחת ליכולת המדידה הידועה כיום, ולכן מאובחנים בטעות כבעלי התנגדות חשמלית אפסית).

דיאמגנטיות

ערך מורחב – אפקט מייסנר

מבחינת מוליכותו החשמלית, מוליך-העל זהה למוליך אידיאלי אך בפועל, מוליך-העל נבדל ממוליך אידיאלי בתכונת הדיאמגנטיות המושלמת: שדה מגנטי חיצוני כמעט שאיננו יכול לחדור לתוך מוליך-על, מעבר למרחק מסוים, בעוד ובמוליך אידיאלי ייתכן מצב של שדה מגנטי שאיננו מתאפס.

לפי חוק לנץ, כל שינוי בשדה החיצוני המופעל על מוליך גורם להופעת זרמים המבטלים את השפעתו. עם זאת, במוליך רגיל, התנגדותו החשמלית גורמת לדעיכתם של זרמים אלו ולכן מופיע שדה מגנטי בחומר. במוליך אידיאלי, לעומת כך, זרמים אלו לא ידעכו בהיעדר התנגדות ולכן לא ניתן לשנות את השטף המגנטי דרך מוליך אידיאלי. בפרט, אם המוליך האידיאלי נמצא בראשית בתנאים בהם אין שדה מגנטי ואז מופעל שדה מגנטי חיצוני, השדה המגנטי לא יחדור אליו בתהליך זה. לו היה מוליך מסוים מצוי בתנאים של שדה מגנטי ואז מקורר לתנאי מוליך-אידיאלי, שדה מגנטי זה היה "נכלא" בתוכו. מתמטית, טענה זו נסמכת על חוק פאראדיי: עבור טבעת מוליכה בשטח A עם השראות L והתנגדות R הנמצאת בשדה חיצוני $B_{0}$ מתקיימת הנוסחה $-A{\frac {dB_{0}}{dt}}=L{\dot {I}}+RI$. עבור R=0, נוסחה זו שקולה למעשה לקשר $\ AB_{0}+LI={\text{const}}$.

עם זאת, כאשר נערך ניסוי בו הופעל שדה מגנטי חיצוני על חומר שקורר למוליך-על, גם אם היה קיים בו שדה בראשית התהליך לפני שקורר עד לטמפרטורה בה הפך למוליך-על, התקבלו תוצאות השונות מאלו של מוליך אידיאלי: כאשר הונח חומר מתאים בשדה מגנטי וקורר עד למצב של מוליך-על, השדה בעומק מוליך העל התאפס. באופן כללי, בניגוד למוליך אידיאלי, מוליך-על כמעט שלא מאפשר לשדה מגנטי לחדור לתוכו, מעבר לסקלת אורך אופיינית מסדר גודל של עשרות או מאות ננומטרים, המסומנת $\ \lambda$. לכן, במקרה של מוליכי-על מקרוסקופיים, נוהגים לרוב להניח כי השדה הוא פשוט אפסי בתוך מוליך-העל. תופעה זו נקראת "אפקט מייסנר". תיאור החדירה של שדה מגנטי לתוך מוליך-על נתון בנוסחה הבאה, הנקראת "משוואת לונדון".

$\nabla ^{2}\mathbf {B} ={\frac {1}{\lambda ^{2}}}\mathbf {B} ,\qquad \lambda \equiv {\sqrt {\frac {mc^{2}}{4\pi n_{s}e^{2}}}}$

פתרונותיה של משוואה זו הם תלויי גאומטריה, אך מצביעים ככלל על דעיכה חזקה מאוד של השדה המגנטי בתוך החומר בנוכחות שדה חיצוני, באשר $\ \lambda$ הוא עומק אופייני לחדירת השדה.

מוליכי על מסוג ראשון ושני

החל מערך מסוים של שדה מגנטי ואילך, נפסקת יכולת מוליכות-העל של החומר. ניתן להצדיק תופעה זו מתמטית משיקולים תרמודינמיים (מציאת ערך מזערי של אנרגיה חופשית של גיבס). בתהליך זה מתחיל החומר להיפרד לשתי פאזות: פאזת מוליכות-על ופאזה "רגילה" של מוצק בעל התנגדות סופית.

בתווך בין שני החלקים, הנמצאים בשיווי משקל תרמודינמי, אצורה אנרגיית שטח. ישנם חומרים בהם אנרגיית השטח שלילית ולכן בתנאים מסוימים, מתחת לטמפרטורה והזרם הקריטיים ובין שני ערכים של שדה מגנטי, הם נוטים להפרד למצב ביניים בין מוליכות-על למצב רגיל, הנקרא "מצב מעורב", בו האנרגיה החופשית של גיבס קטנה יותר הן ממצב רגיל והן ממצב מוליך-על. ההיפרדות של חומרים אלו היא למצב בו החומר מופרד לתאים קטנים רבים, קטנים בהרבה מהסקאלה המאפיינת את מעבר הפאזה במוליכי-על עם אנרגיית שטח חיובית.

• לחומרים עם אנרגיית שטח חיובית ישנו, כאמור, ערך יחיד של שדה מגנטי קריטי שעבור שדה החזק ממנו החומר לא יהיה עוד מוליך-על. חומרים אלו נקראים "מוליכי-על מהסוג הראשון".
• לחומרים עם אנרגיית שטח שלילית, קיימים שני ערכים קריטיים של השדה המגנטי שבהם מתרחש מעבר פאזה: נקודה קריטית נמוכה שמתחת לה נמצא החומר במצב של מוליך-על רגיל, ונקודה קריטית שמעליה לה נמצא המוליך במצב רגיל. ביניהן נמצא החומר במצב של פאזה מעורבת, בה נפרד החומר לתאים-תאים קטנים. חומרים אלו נקראים "מוליכי-על מהסוג השני".

השדה הקריטי של מוליכי על מהסוג הראשון, וכן של השדה הראשון של מוליכי על מסוג שני, הוא נמוך יחסית - סדר גודל של 100–1000 גאוס. לעומת זאת, השדה הקריטי השני של מוליכי על מהסוג השני גבוה בהרבה, עד כדי 2–3 סדרי גודל, כלומר, כמה אלפי קילו-גאוס. מסיבה זו, משתמשים בדרך כלל במוליכי על מסוג שני על מנת ליצור שדות מגנטיים חזקים מאוד, למשל ב-MRI, וזאת מאחר שהם יכולים להפיק אותם על ידי זרמים חזקים מאוד שיזרמו דרכם, וזאת מבלי להשקיע אנרגיה גבוהה במיוחד ביצירת הזרמים.

אפיון תרמודינמי

דיאגרמת פאזות של מוליך-על מהסוג הראשון. מצבים הכלואים בין המשטח האפור לבין הצירים הם מצבים בהם מתקיימת מוליכות-על.

הטמפרטורה, השדה המגנטי החיצוני והזרם הזורם במוליך-העל משנים את האנרגיה בתוכו כך שמעבר לערכים קריטיים מסוימים מצב מוליכות-העל נפסק משום שאיננו עוד עדיף אנרגטית על המצב הרגיל. במרחב התלת הממדי של טמפרטורה, זרם, ושדה ניתן להגדיר "נפח מוליכות-על" כך שעבור צירוף פרמטרים המתאים לנקודה הכלואה בנפח, החומר יהיה בפאזת מוליכות-על. דיאגרמת הפאזות המתאימה לעל מוליכים מהסוג הראשון מובאת באיור משמאל.

תלות של קיבול החום וההתנגדות הסגולית של החומר בטמפרטורה שלו

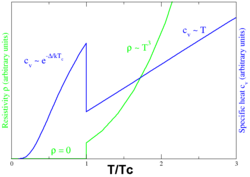
במוליכים, כמו גם בחומרים בעלי תכונות מוליכות-על מעבר לטמפרטורה הקריטית, קיבול החום האלקטרוני של החומר פרופרציוני לטמפרטורה. מעבר הפאזה מלווה בקפיצה אופיינית בקיבול החום של החומר שהופכת לתלות אקספוננציאלית בטמפרטורה, כמתואר בגרף משמאל.

שאלת קיומו של חום כמוס בתהליך מעבר הפאזה המאפיין מוליכות-על ואפיון מעבר הפאזה (היינו – קביעה האם מעבר פאזה זה הוא מסוג ראשון או שני, להרחבה ראו מעבר פאזה) הייתה שאלה פתוחה עד שבשנות ה-80 של המאה ה-20 נקבע הן ניסויית והן תאורטית שמוליכי-על מסוג ראשון עוברים מעבר פאזה מסוג ראשון המלווה בחום כמוס ושמוליכי על מסוג שני עוברים מעבר פאזה מסוג שני וללא חום כמוס.

הסבר לתופעה

אפקט האיזוטופ וחשיבות הסריג

הניסיון מראה כי גם בין איזוטופים שונים של אותו החומר קיימת שונות בטמפרטורת המעבר הקריטית. מכך ניתן להסיק כי התאוריה של מוליכות-על צריכה להתייחס לא רק אל נושאי המטען בחומר, אלא אף לאופי הסריג, ובפרט לאופי היונים המאכלסים אותו. לכן, תאוריה מיקרוסקופית של מוליכות-על צפויה להתייחס גם לתכונותיו של הסריג. בהתאם לצפי זה, פרמטרים רבים של תורת BCS שתתואר בפסקה הבאה המתארת את תופעת מוליכות-העל בצורה מיקרוסקופית תלויים בתדירות אופני התנודה העצמיים של הגביש.

תאוריית BCS

תאוריית BCS למוליכות-על הוצעה בשנת 1957 על ידי המדענים ג'ון ברדין, ליאון קופר וג'ון שרייפר, שעיקרה היא היווצרות קוונטית של זוגות קופר על ידי פוטנציאל משיכה בין האלקטרונים, שנובע מתוך תנאי הסריג והרעידות שלו (פונונים).

בגביש מעשי, מקור תופעת ההתנגדות החשמלית הוא בכך שהאלקטרונים נעים בחומר ומתפזרים ממנו. תמונה מיקרוסקופית של פיזור זה מתארת עירור של אופן תנודה בגביש המתבטא בשחרור פונון, שהוא ערעור בדיד של גל קול בגביש, המקביל לפוטון בגל האור. ייתכן מצב שבו הפונון ששוחרר על ידי חלקיק מסוים ייקלט על ידי חלקיק אחר באינטראקציה מושכת. באופן כללי, ללא ההפרעה, רמת היסוד של שני האלקטרונים היא אנרגיית פרמי, משום שלפי עקרון פאולי הם אינם יכולים לאכלס רמות אנרגיה נמוכות יותר (בטמפרטורה סופית, קביעה זו נכונה רק בקירוב, אך זהו קירוב טוב יחסית משום שטמפרטורת החדר נמוכה בהרבה מטמפרטורת פרמי האופיינית למתכות). רמת היסוד של הזוג מושפעת מן האינטראקציה של החלפת פונונים כך שפיזור של הצמד מהגביש, אם יתרחש, ניתן לקירוב כהפרעה קטנה ולכן לפי תורת ההפרעות הקוונטית, יגרום להורדת רמת היסוד של הצמד אל מתחת לרמת פרמי.

אם לאלקטרונים גם ספין הפוך, אזי הזוג הנוצר הוא בוזון ולכן לא חייב לקיים את עקרון האיסור של פאולי, ולכן לאחר פיזורים יכולים להתקיים בו זמנית זוגות רבים שהאנרגיה שלהם יכולה להגיע למינימום שהוא אף מתחת לפעמיים אנרגיית פרמי. ניתן להראות כי כאשר התנע הכולל הוא אפס, היינו – לאלקטרונים תנעים בכיוונים מנוגדים, ייווצרו הזוגות הרבים ביותר. לכן, זהו המצב המועדף אנרגטית ולכן נוצרים בחומר צמדים מסוג זה. צמד של אלקטרונים הנמשכים זה לזה בקשר מסוג זה נקראים "צמד קופר". ההגבלה היחידה על מספר הצמדים בחומר נובעת מעקרון האיסור של פאולי, המגביל את מספר המצבים האפשריים של שני אלקטרונים מנוגדי תנע וספין במתכת, בטרם נוצרו הזוגות.

אוסף הצמדים הוא מעין "זורם בוז-איינשטיין מעובה" בטמפרטורות נמוכות דיין. מה קורה אם המערכת נמצאת בטמפרטורה נמוכה בה עברו כל הזוגות עיבוי בוז-איינשטיין? כאשר הזוג עובר פיזור מאלמנט שריג, אם אנרגיית הפיזור קטנה מפער האנרגיה עד לרמת האנרגיה הבאה של הזוג, אזי המפזר לא יכול לשנות את התנע והאנרגיה של הזוג ובכך לשבור אותו (בדומה לאלקטרון המאכלס את רמת היסוד באטום, אך לא מאבד בה אנרגיה עקב האצה). האנרגיה שיכול להעביר המפזר לזוג נקבעת לפי האנרגיה הקינטית של אלמנטי המפזר שהיא, למעשה, אנרגיית חום. לכן, על מנת לשמר את זוגות הקופר במערכת, יש לשמור את המערכת מתחת לרף טמפרטורה מסוים.

אם במצב זה, מסיבה מסוימת, מוסט התנע הממוצע של האלקטרונים בגביש בוקטור תנע קבוע, מרכז המסה של כל צמד קופר ינוע בממוצע עם וקטור התנע המוסט, כאשר התנע והאנרגיה הכוללים של כל זוג לא יכולים להשתנות כיוון שלשם כך יש לעורר את הזוג ולשבור אותו. זרם שכזה, אם לא תשונה האנרגיה של המערכת, יכול להמשיך ללא הפרעה בלא הגבלה של זמן ולכן ההתנגדות החשמלית של החומר מתאפסת.

עולה השאלה – מדוע אלקטרוני ההולכה בחומר, הנמצאים בו בה-בעת עם זוגות הקופר, אינם גורמים לקיומה של התנגדות במערכת? ניתן להתייחס אל מודל המתאר את המערכת הנדונה כסריג המוקף "נוזל-על" של זוגות קופר וגז אלקטרונים "רגילים". כאשר מחברים שני הדקי מקור מתח לדגם, הרי שהדבר דומה לשני נגדים המחוברים במקביל בין הדקי המקור – נגד עם התנגדות אפסית המייצג את אוסף זוגות הקופר ונגד בעל התנגדות סופית הגדולה מאפס המייצג את אלקטרוני ההולכה אשר פיזוריהם גורמים להפסדי האנרגיה. במצב זה, לפי חוקי החשמל, הזרם יזרום במלואו דרך הנגד שהתנגדותו אפסית, היינו – "על הנוזל" של זוגות הקופר.

תאוריית גינצבורג לנדאו

ויטאלי גינזבורג ולב לנדאו הציעו תאוריה מקרוסקופית לתיאור מוליכי-על בה הניחו שני פרמטרים המתארים את החומר וכן פרמטר חופשי מרוכב, אותו סימנו באות היוונית פסי ($\ \psi$) שהוא פרמטר הגודל של הבעיה. מנקודת מבט מודרנית, בהנחה כי נושאי המטען – הם זוגות קופר – יוצרים נוזל-על, הרי שמשמעותו של $\ |\psi |^{2}$ היא החלק היחסי מכלל האלקטרונים בחומר שהם זוגות קופר. ניתוח הדורש מציאת ערך מזערי של האנרגיה החופשית בנוכחות שדה חיצוני, אותה פיתחו עד סדר רביעי בפרמטר הגודל $\ \psi$, מניב תלות בשני פרמטרים חשובים, הם עומק החדירה $\ \lambda$ שהוזכר לעיל במסגרת הדיון במשוואות לונדון (אף כי במסגרת תורה זו הוא מבוטא על ידי הפרמטרים של תורת גינצבורג-לנדאו) וכן פרמטר נוסף – אורך הקוהרנציה $\ \xi$ – שבמונחים מודרניים מבטא את סדר הגודל של אורכם של זוגות קופר. היחס ביניהם $\varkappa \equiv {\frac {\lambda }{\xi }}$ נקרא "פרמטר גינצבורג-לנדאו". תוצאה חשובה של התאוריה קובעת האם על מוליך מסוים הוא מסוג ראשון או שני בתלות בערכו של פרמטר זה: אם $\varkappa <{\frac {1}{\sqrt {2}}}$, החומר הוא מוליך-על מהסוג הראשון, אחרת – מהסוג השני.

מוליכי-על בטמפרטורה גבוהה

ערך מורחב – מוליכות-על בטמפרטורות גבוהות

פרק זה טעון עדכון. אנא תרמו למכלול ועזרו לעדכן אותו. הסיבה היא ב2020 התגלה חומר שהופך למוליך על בטמפרטורה גבוהה בלחץ גבוה.

מוליכות-העל שנדונה בסעיפים קודמים והסברה בצורה מיקרוסקופית על ידי תאוריית BCS מתקיימת בטמפרטורות נמוכות יחסית, כאשר הגבול התאורטי שהוערך בו תוכל מוליכות-על להתקיים לפי תאוריית BCS הוא 30 קלווין. עם זאת, בחלוף הזמן התגלו גם חומרים המגלים תכונות של מוליכות-על אף בטמפרטורות גבוהות יותר, חלקן אף גבוהות יותר מטמפרטורת הרתיחה של חנקן, היא 77 קלווין. לאלו האחרונים חשיבות רבה מבחינה טכנולוגית, שכן קירור בעזרת חנקן נוזלי הוא יחסית זול ופשוט. למשל, טמפרטורת המעבר של החומר YBa₂Cu₃O₇, המכונה לעיתים YBCO, היא 93 קלווין. חומרים אלו נקראים "מוליכי-על בטמפרטורה גבוהה". כיום, לא ידוע מהו המנגנון הגורם לתופעת המוליכות בחומרים אלו ובעיה זו היא מבין הבעיות הפתוחות המשמעותיות בפיזיקת מצב מוצק. בפרט, נשאלת השאלה האם ישנו ערך עליון לטמפרטורה הקריטית של מוליכי על והאם ישנם מוליכי על אשר הטמפרטורה הקריטית שלהם היא מסדר גודל של טמפרטורת החדר, או אף מעליה, שכן מוליכות-על בטמפרטורת החדר יכולה להיות בעלת שימושים טכנולוגיים רבים.

שימושים

פרק זה לוקה בחסר. אנא תרמו למכלול והשלימו אותו.

סלילים של מוליכי-על יכולים ליצור שדות מגנטיים חזקים למדי שאינם דועכים עקב אי דעיכתו של הזרם הזורם ללא התנגדות. לפיכך, אלקטרומגנטים מבוססי מוליכי-על הם יעילים למדי ומשמשים במספר התקנים בהם נדרשים שדות מגנטיים חזקים, כמו מכשירי תהודה מגנטית גרעינית, דימות תהודה מגנטית, רכבות ריחוף מגנטי ומאיצי חלקיקים.

לאפקט ג'וזפסון, בו זורם זרם דרך שני מוליכי-על שביניהם מבודד (תצורה הנקראת "צומת ג'וזפסון"), מספר שימושים גם כן. התקנים הנעזרים בצמתי ג'וזפסון משמשים כבסיס למגנטומטרים רגישים ולטכנולוגיה הנעזרת בהם, כמו דימות של זרמים חלשים או חלקיקים מגנטיים על פני משטחים.

מעברי הפאזה האופייניים למוליכי-על, כמו גם תכונות קווינטוט אופייניות של הזרמים מוליכי-העל משמשים לצורכי מיתוג וחישה. כך, למשל, במערכת הכריוטרון המשמשת לבקרת זרם, זרימת זרם מעבר לסף מסוים תשרה שדה מגנטי העולה על השדה הקריטי של מוליך-על בו עובר זרם בקרה ותורה למערכת הבקרה על חריגה מהזרם הקריטי.

מקורות

• A. C. Rose-Innes and E. H. Rhoderick, Introduction to Superconductivity, (Pergamon Press, Oxford, 1978)

קישורים חיצוניים

שגיאות פרמטריות בתבנית:ויקישיתוף בשורה
פרמטרי חובה [ שם ] חסרים

מדיה וקבצים בנושא מוליכות-על בוויקישיתוף

• TED,ריחוף של מוליך על, באתר Ted
• מגזין מכון ויצמן, מוליכות על, באתר ynet
• הידען-פיזיקה, מוליך על, באתר הידען
• מדע מהיר, מהי מוליכות-על?, באתר ynet
• דן שחר, ‏להעלים את ההתנגדות, אודיסאה 13, אוקטובר 2011
• 
  שגיאות פרמטריות בתבנית:בריטניקה
  פרמטרי חובה [ 1 ] חסרים

הערות שוליים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

32650459מוליכות-על