גז פרמי

גז פרמי הוא גז קוונטי המתאר מערכת של פרמיונים זהים ללא אינטראקציה. פרמיון הוא חלקיק בעל ספין חצי שלם (בניגוד לבוזון לו יש ספין שלם) כמו אלקטרון, פרוטון ונייטרון המתנהג בהתאם להתפלגות פרמי-דיראק. פונקציה זו מתארת את תכונות והתנהגות החלקיקים בשיווי משקל תרמודינמי בהינתן הטמפרטורה, הפוטנציאל הכימי ומצבי האנרגיה האפשריים של המערכת. מודל זה פותח בהתאם לעקרון האיסור של פאולי המהווה בסיס להבנת תכונות הפרמיונים ונקרא על שם הפיזיקאי האיטלקי אנריקו פרמי.

למודל זה שימושים רבים בעקבות ההתאמה הטובה למערכות שונות בטבע. התנהגות האלקטרונים במתכת וכן האלקטרונים הנמצאים בננס לבן מתנהגים בהתאם למודל של גז פרמי.

עקרון האיסור של פאולי

על פי מכניקת הקוונטים, מערכת של חלקיקים ניתנת לתיאור על ידי פונקציית גל רב חלקיקית המתארת את המספרים הקוונטים של המערכת. לדוגמה, בהינתן שני חלקיקים, ניתן לתארם על ידי פונקציית הגל: $\Psi (A,B)$ או ביותר פירוט $\Psi ({\vec {r_{A}}},{\vec {k_{A}}},{\vec {r_{B}}},{\vec {k_{B}}})$, כאשר ${\vec {r_{A}}}$ ,${\vec {k_{A}}}$ מתארים את בהתאמה את המיקום והתנע של חלקיק $A$, ובאתו האופן ${\vec {r_{B}}}$ ,${\vec {k_{B}}}$ מתארים את חלקיק $B$.
ע"פ ההגדרה, פרמיונים הם חלקיקים אנטי-סימטריים להחלפה. כלומר בהחלפת חלקיק $A$ בחלקיק $B$, מתקבל כי פונקציית הגל משנה את סימנה: $\Psi (A,B)=-\Psi (B,A)$. מכך נובע שאם מחליפים שני פרמיונים בעלי מספרים קוונטים זהים ${\vec {r_{A}}}={\vec {r_{B}}},{\vec {k_{A}}}={\vec {k_{B}}}$ מקבלים כי $\Psi ({\vec {r_{A}}},{\vec {k_{A}}},{\vec {r_{A}}},{\vec {k_{A}}})=-\Psi ({\vec {r_{A}}},{\vec {k_{A}}},{\vec {r_{A}}},{\vec {k_{A}}})$, דבר המתאפשר רק אם $\Psi \equiv 0$ .

כלומר שני פרמיונים אינם יכולים להימצא באותו מצב קוונטי בו-זמנית (בניגוד לבוזונים היכולים לעבור עיבוי בוז-איינשטיין). מסקנה זו היא שהובילה לפיתוח התפלגות פרמי-דיראק המהווה בסיס למודל של גז פרמי.

התפלגות פרמי-דיראק

התפלגות פרמי-דיראק עבור טמפרטורות שונות

בהתאם להבנה כי כל מצב קוונטי יכול לאכלס פרמיון בודד, פותחה סטטיסטיקת פרמי-דיראק. פונקציה זו מתארת את התפלגות החלקיקים במערכת המצומדת לאמבט חום בטמפרטורה $T$ ואמבט חלקיקים בעל פוטנציאל כימי $\mu$. בהינתן מצב קוונטי בודד, ניתן לחשב את פונקציית החלוקה של המצב בצבר הגראנד קנוני על ידי אכלוס ריק או אכלוס יחיד עם אנרגיה $\epsilon$:

${\mathcal {Z}}={1+e^{-(\epsilon -\mu )/k_{B}T}}$

בעזרת פונקציית החלוקה החד-חלקיקית, אפשר לקבל את האכלוס הממוצע של כל מצב (בעל אנרגיה $\epsilon$ מתאימה) על ידי התפלגות פרמי-דיראק:

${\mathcal {f}}_{FD}(\epsilon ,\mu ,T)={\frac {1}{e^{(\epsilon -\mu )/k_{B}T}+1}}$

לפי ביטוי זה, ככל שהטמפרטורה הולכת וקטנה, ההתפלגות נהיית יותר ויותר חדה. כאשר הטמפ' שואפת ל-0, מתקבל כי כל מצבי האנרגיה הקטנים מהפוטנציאל הכימי $\mu$ מאוכלסים, בעוד המצבים בעלי אנרגיה הגדולה מערך זה ריקים. מצב זה נקרא גז פרמי מנוון. במצב ההפוך, בו הטמפרטורה גדולה מאוד, פונקציית החלוקה הולכת וקרבה לאפס והאכלוס נהיה דליל. גבול זה הוא הגבול בו הגז נהיה אידיאלי קלאסי (במצב של אכלוס דליל רוב המצבים הקוונטים אינם מאוכלסים ולכן אין סתירה לעקרון האיסור של פאולי).

נהוג להגדיר את הגבול הקלאסי עבור צפיפות חלקיקים המקיימת $\left\langle n\right\rangle \ll n_{Q}$, כאשר $n_{Q}=\left({\frac {2\pi mk_{B}T}{h^{2}}}\right)^{\frac {3}{2}}$ היא הצפיפות הקוונטית.

בעזרת ההתפלגות ניתן לחשב גדלים כמו מספר החלקיקים או האנרגיה הכוללת של המערכת. בחישובים אלה יש לקחת בחשבון את צפיפות המצבים $D(\epsilon )$.

צפיפות המצבים

כאשר פותרים את הבעיה של חלקיק בקופסה בעל יחס תנע-אנרגיה $\epsilon ={\frac {p^{2}}{2m}}$ מקבלים כי האנרגיות האפשריות של החלקיק נתונות על ידי: $\epsilon _{n}={\frac {\hbar ^{2}}{2m}}{\frac {\pi ^{2}}{L^{2}}}n^{2}$, כאשר $n={\sqrt {n_{x}^{2}+n_{y}^{2}+n_{z}^{2}}}$.
עבור ערכי $n$ גדולים, מקבלים כי יש מספר רב של ערכי $n_{x},n_{y},n_{z}$ אשר יתנו את אותו $n$. כלומר, מתקבלים אותן רמות אנרגיה עבור ערכי $n_{x},n_{y},n_{z}$ שונים ונוצר ניוון בבעיה. בהתאם לכך, צפיפות המצבים $D(\epsilon )$ סופרת את מספר המצבים הנמצאים בתחום האנרגיות $(\epsilon ,\epsilon +d\epsilon )$ ומאפשרת לקחת בחשבון את הניוון בעת חישובים של פרמטרים שונים של המערכת.

ישנן שתי דרכים עיקריות לחישוב $D(\epsilon )$:

סכימה על המצבים החד-חלקיקיים

כמתואר לעיל, אנרגיית החלקיק תלויה במספרים הקוונטים $n_{x},n_{y},n_{z}$ . על כן, יש לחפש תחילה את כמות המצבים חד-חלקיקיים עם אנרגיה קטנה מ- $\epsilon$: $g(\epsilon )\equiv \int _{-\infty }^{\epsilon }D(\epsilon )\,d\epsilon$ .

לדוגמה, עבור פרמיון בעל ספין כללי $j$ בשלושה ממדים, ניתן לחשב ערך זה על ידי חישוב הנפח של כדור ברדיוס $n(\epsilon )$ במרחב התלת-ממדי $n_{x},n_{y},n_{z}$. בעזרת שימוש בביטוי לאנרגיות האפשריות של המערכת, ניתן לבודד את מספר המצבים $n$ כפונקציה של האנרגיה וגודל הקופסה:

$\epsilon _{n}={\frac {\hbar ^{2}}{2m}}{\frac {\pi ^{2}}{L^{2}}}n^{2}\Rightarrow n(\epsilon )={\frac {L}{\pi }}\left({\frac {2m\epsilon }{\hbar ^{2}}}\right)^{1/2}$

ערך זה משמש כרדיוס במרחב התלת-ממדי $n_{x},n_{y},n_{z}$. בעזרתו אפשר לחשב את מספר המצבים הקוונטים הכולל של המערכת עד אנרגיה $\epsilon$, על ידי חישוב הנפח של כדור ברדיוס $n(\epsilon )$:

$g(\epsilon )=\left(2j+1\right){\frac {1}{8}}{\frac {4\pi }{3}}\left[n(\epsilon )\right]^{3}=\left(2j+1\right){\frac {V\left(2m\epsilon \right)^{\frac {3}{2}}}{6\pi ^{2}\hbar ^{3}}}$

כאשר:

• הפקטור $2j+1$ מתאר את הניוון הנובע מהספין.
• הפקטור ${\frac {1}{8}}$ מתאר סכימה של ערכי $n_{x},n_{y},n_{z}$ חיוביים בלבד.

צפיפות המצבים כפונקציה של האנרגיה עבור חלקיק חופשי בשלושה ממדים

על-מנת לחשב את צפיפות המצבים, המתארת את מס' המצבים ליחידת אנרגיה הנמצאים בתחום אנרגיות אינפיניטסימלי, יש להסתכל על מספר המצבים החד החלקיקים הנמצא בתחום $(\epsilon ,\epsilon +d\epsilon )$ . מספר המצבים מתואר על ידי ההפרש $g(\epsilon +d\epsilon )-g(\epsilon )$ ולקבלת הצפיפות יש לחלק בגודל התחום:

$D(\epsilon )={\frac {g(\epsilon +d\epsilon )-g(\epsilon )}{d\epsilon }}={\frac {dg(\epsilon )}{d\epsilon }}$

כלומר:

$D(\epsilon )=\left(2j+1\right){\frac {V\left(2m\right)^{\frac {3}{2}}}{4\pi ^{2}\hbar ^{3}}}\epsilon ^{\frac {1}{2}}\propto \epsilon ^{\frac {1}{2}}$

סכימה במרחב הפאזה

דרך נוספת לחישוב צפיפות המצבים היא בעזרת סכימה על מרחב הפאזה. בדומה לגז אידיאלי, מצב קוונטי אינפיניטסימלי מתואר על ידי ריבוע במרחב $x,p$ . בהתאם לעקרון האי-ודאות, גדול הריבוע המינימלי למצב זה הוא $\Delta x\Delta p\sim h$ ועל כן, צפיפות המצבים הבסיסית במרחב הפאזה עבור חלקיק תלת-ממדי היא ${\frac {1}{h^{3}}}$. לכן, קטע אינפיניטסימלי של אנרגיה ניתן להבעה על ידי:

$D(\epsilon )d\epsilon ={\frac {d^{3}x\cdot d^{3}p}{h^{3}}}\cdot I$

כאשר $I$ נובע מהניוון במרחב הפאזה, ו-$D(\epsilon )$ מסמן את הניוון בתחום האנרגיה הנתון.

עבור חלקיק חופשי לא יחסותי, לו האנרגיה אינה תלויה במיקום, ניתן להחליף $d^{3}x\rightarrow V$ ( האנרגיה אינה תלויה במיקום ותיסכם כנפח באינטגרל) וכל שנותר הוא לפשט את הגודל $d^{3}p$.
במעבר לקואורדינטות כדוריות, $d^{3}p\rightarrow 4\pi p^{2}dp$ ובעזרת שימוש בקשר תנע-אנרגיה של חלקיק חופשי מתקבל כי $dp={\frac {m}{p}}d\epsilon$ . הצבה של הערכים חזרה למשוואה המקורית מניבה:

$D(\epsilon )d\epsilon =I{\frac {4\pi Vm^{\frac {3}{2}}2^{\frac {1}{2}}}{h^{3}}}\epsilon ^{\frac {1}{2}}d\epsilon \Rightarrow D(\epsilon )=\left(2j+1\right){\frac {V\left(2m\right)^{\frac {3}{2}}}{4\pi ^{2}\hbar ^{3}}}\epsilon ^{\frac {1}{2}}$

כאשר נעשה שימוש בהמרה של קבוע פלאנק: $\hbar \equiv {\frac {h}{2\pi }}$ ובכך שהניוון $I$ נובע מהספין ועל כן שווה ל- $2j+1$.

בעזרת פונקציית צפיפות המצבים, ניתן לחשב גדלים מקרוסקופיים של המערכת כמו מספר החלקיקים הממוצע או האנרגיה הממוצעת:

$\left\langle N\right\rangle =\int D(\epsilon ){\mathcal {f}}_{FD}(\epsilon )d\epsilon$
$\left\langle U\right\rangle =\int \epsilon D(\epsilon ){\mathcal {f}}_{FD}(\epsilon )d\epsilon$

גז פרמי מנוון

כמתואר לעיל, לפונקציית ההתפלגות תלות בטמפרטורת המערכת. ניתן לראות כי כאשר $T\rightarrow 0$ תלות זו נהיית קריטית וההתפלגות נהיית חדה. עבור ערכי אנרגיה $\epsilon <\mu$ מתקבל כי ${\mathcal {f}}_{FD}(\epsilon )\rightarrow 1$, כלומר כל המצבים עם אנרגיה קטנה מערך זה מאוכלסים. לעומת זאת, עבור $\epsilon >\mu$ מתקבל כי ${\mathcal {f}}_{FD}(\epsilon )\rightarrow 0$, כלומר מצבים אלו אינם מאוכלסים כלל. אכלוס זה הוא תוצאה ישירה מכך ששני פרמיונים אינם יכולים לאכלס את אותו המצב הקוונטי ועל כן עולים למצב האפשרי הבא. הם ממשיכים כך עד אשר ימלאו את כל המצבים האפשריים לרמת האנרגיה הנתונה.

נהוג להגדיר אנרגיה זו בתור אנרגיית פרמי $\epsilon _{F}$: האנרגיה בה כל המצבים בעלי אנרגיה נמוכה ממנה מאוכלסים כאשר $T\rightarrow 0$. זהו מצב היסוד של המערכת הרב-חלקיקית.

ניתן לחשב אנרגיית פרמי עבור גז פרמיונים המכיל $N$ חלקיקים חופשיים בשלושה ממדים בדומה לדרך בה חושבה כמות המצבים חד-חלקיקיים $g(\epsilon )$. מספר החלקיקים הכולל מתואר על ידי נפח כדור ברדיוס $n_{F}$ המכיל את המספרים הקוונטים של כל החלקיקים ועל כן סוכם את כל חלקיקי המערכת:

$N=(2j+1)\cdot {\frac {1}{8}}\cdot {\frac {4\pi }{3}}n_{F}^{3}\Rightarrow n_{F}=\left({\frac {6N}{(2j+1)\pi }}\right)^{\frac {1}{3}}$

כאשר:

• הפקטור $2j+1$ מתאר את הניוון הנובע מהספין.
• הפקטור ${\frac {1}{8}}$ מתאר סכימה של ערכי $n_{x},n_{y},n_{z}$ חיוביים בלבד.

האנרגיה של החלקיקים נתונה על ידי $\epsilon _{n}={\frac {\hbar ^{2}}{2m}}{\frac {\pi ^{2}}{L^{2}}}n^{2}$ ועל כן אנרגיית פרמי היא:

$\epsilon _{F}\equiv {\frac {\hbar ^{2}}{2m}}{\frac {\pi ^{2}}{L^{2}}}n_{F}^{2}={\frac {\hbar ^{2}}{2m}}\left({\frac {6\pi ^{2}N}{(2j+1)V}}\right)^{\frac {2}{3}}$

עם שימוש בערך זה ניתן לחשב את האנרגיה הממוצעת של גז אלקטרונים בעלי ספין 1/2:

$U(T=0)=\int \epsilon D(\epsilon ){\mathcal {f}}_{FD}(T=0,\epsilon )d\epsilon =\int _{0}^{\epsilon _{F}}\epsilon D(\epsilon )d\epsilon ={\frac {3}{5}}N\cdot \epsilon _{F}\propto V^{-{\frac {2}{3}}}$

כאשר מתקיים ${\mathcal {f}}_{FD}(T=0,\epsilon )\equiv 0$ עבור $\epsilon >\epsilon _{F}$.

על-מנת לחשב את הלחץ, יש להשתמש באנרגיה החופשית של המהולץ הנתונה על ידי $F=U-TS$. במצב בו $T\rightarrow 0$ מתקבל כי $F=U$ ובעזרת שימוש בקשר $\ P=-\left({\frac {\partial F}{\partial V}}\right)_{S}=-\left({\frac {\partial U}{\partial V}}\right)_{S}$ ניתן לחשב את הלחץ:

$P={\frac {2}{5}}{\frac {N}{V}}E_{\mathrm {F} }={\frac {(3\pi ^{2})^{\frac {2}{3}}\hbar ^{2}}{5m}}\left({\frac {N}{V}}\right)^{5/3}$

יחס המסה-רדיוס בננס לבן. מעבר לצפיפות גבוהה מצריך שימוש במודל היחסותי. מסת צ'נדראסקאר מסומנת M_Ch .

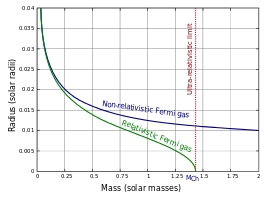
כלומר בניגוד גז אידיאלי קלאסי, הלחץ אינו מתאפס בטמפרטורה $T\rightarrow 0$. לחץ זה נקרא לחץ הניוון והוא מונע מחלקיקים להידחס לנפחים קטנים יותר. תופעה זו היא שגורמת לננס לבן (אשר ניתן להתייחס אליו כמורכב מגז פרמי מנוון של אלקטרונים) לא לקרוס על אף כוח המשיכה הפועל עליו. כוח המשיכה גורם לדחיסת החומר בכוכב ומוביל לעלייה בכמות האלקטרונים ליחידת נפח. שימוש בעקרון אי הוודאות עבור מיקום-תנע מראה שהקטנת הנפח תביא לעליה באנרגיה הקינטית של החלקיקים ועל כן גם לעלייה בלחץ. לחץ זה גדל עד אשר הוא משתווה לכוח הכבידה ומונע מהכוכב להתמוטט לכוכב נייטרונים או לחור שחור.

יש להדגיש כי עם עליית האנרגיה הקינטית, מהירות החלקיקים עולה ויש לקחת אפקטים יחסותיים בחשבון. על-מנת לנתח את המערכת במצב זה יש להשתמש בקשר תנע-אנרגיה של חלקיק יחסותי המתואר בהמשך.

בעזרת אנרגיית פרמי, נהוג להגדיר גם את טמפרטורת פרמי על ידי: $T_{F}\equiv {\frac {\epsilon _{F}}{k_{B}}}$.

זוהי הטמפרטורה הקובעת את סקלת הבעיה. כלומר עבור טמפרטורות המקיימות $T\ll T_{F}$ ניתן להתייחס למערכת כגז פרמי מנוון. לדוגמה, הטמפרטורה האופיינית בליבת ננס לבן היא $T\thicksim 10^{7}\left[K\right]$ . שימוש בצפיפות הממוצעת ${\bar {n}}\backsim 10^{6}\left[{\frac {gr}{cm^{3}}}\right]$ ובמסת האלקטרון מניבה טמפרטורת פרמי הגדולה מטמפרטורת הכוכב $T_{F}\thicksim 10^{9}\left[K\right]$ . לכן, ניתן להתייחס לאלקטרונים הנמצאים בטמפרטורה גדולה מאפס אך קטנה ביחס ל-$T_{F}$ כגז פרמי מנוון.

גז פרמי יחסותי

עד כה תואר המצב בו יחס התנע-אנרגיה הוא ריבועי, אך ניתן לעשות חישובים דומים גם עבור המקרה היחסותי בו היחס משתנה. על-פי תורת היחסות הפרטית, האנרגיה של חלקיק בודד נתונה על ידי:

$E={\sqrt {(pc)^{2}+(m_{0}c^{2})^{2}}}$

כאשר:

• $m_{0}$ היא מסת המנוחה של החלקיק.
• $c$ היא מהירות האור.

במקרה האולטרה יחסותי, בו $pc\gg m_{0}c^{2}$, ניתן לקרב את ביטוי האנרגיה על ידי:

$E={\sqrt {(pc)^{2}+(m_{0}c^{2})^{2}}}\approx \left|p\right|c$

בעזרת קירוב זה מתקבל קשר ליניארי בין האנרגיה לבין התנע. שימוש באחרון, בקשר $p=hk$ וביחס $k={\frac {\pi n}{L}}$ (המתקבל מתנאי שפה) מאפשר לחשב את הגדלים הרלוונטיים שחושבו עבור גז פרמי לא יחסותי של חלקיקים חופשים, בשינוי יחס הנפיצה.

ערך זה הוא קצרמר בנושא פיזיקה. אתם מוזמנים לתרום למכלול ולהרחיב אותו.

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

32689096גז פרמי