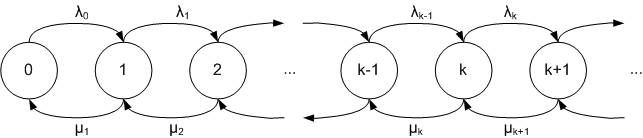
תהליך לידה-מוות

תהליך לידה-מוות הוא שרשרת מרקוב - זמן רציף, המתארת שינוי גודל "אוכלוסיה" כפונקציה של הזמן. גודל ה"אוכלוסיה" (מספר שלם) נקרא המצב של התהליך ויתכנו בו שינויים משני סוגים בלבד: "לידה", המגדיל את המצב באחד ו"מוות", המקטין את המצב באחד. המודל הזה הוצג לראשונה על ידי וויליאם פלר. לתהליכי לידה-מוות יש יישומים רבים בדמוגרפיה, תורת התורים, חקר ביצועים, אפידמיולוגיה, ביולוגיה ותחומים אחרים. ניתן ליישמם, למשל, כדי לחקור אוכלוסיות החיידקים, מספר האנשים החולים במחלה מסויימת בתוך אוכלוסייה, או את מספר הלקוחות בתור בחנות.

הגדרה

תהליך לידה-מוות הוא שרשרת מרקוב זמן רציף $\{X(t),t\geq 0\}$ עם מרחב מצבים $E=\{0,1,\ldots \}$ ושתי סדרות של מספרים ממשיים, קצבי ה"לידות" $\{\lambda _{0},\lambda _{1},\ldots \}$ וקצבי "תמותה" $\{\mu _{1},\mu _{2},\ldots \}$.

במצב $i>0$ זמן השהייה הוא משתנה מקרי מעריכי עם קצב $\lambda _{i}+\mu _{i}$, ההסתברות לעבור למצב $i+1$ היא ${\frac {\lambda _{i}}{\lambda _{i}+\mu _{i}}}$ וההסתברות לעבור למצב $i-1$ היא ${\frac {\mu _{i}}{\lambda _{i}+\mu _{i}}}$.

אם $i=0$ זמן השהייה הוא משתנה מקרי מעריכי עם קצב $\lambda _{0}$ וההסתברות לעבור למצב $i=1$ היא $1$.

תכונות

תנאים להתמדה וזמניות נוסחו על ידי סמואל קרלין וגיימס מקגרגור.

תהליך לידה-מוות הוא מתמיד אם ורק אם מתקיים:

$\sum _{i=1}^{\infty }\prod _{n=1}^{i}{\frac {\mu _{n}}{\lambda _{n}}}=\infty$

תהליך לידה-מוות הוא ארגודי אם ורק אם $\sum _{i=1}^{\infty }\prod _{n=1}^{i}{\frac {\mu _{n}}{\lambda _{n}}}=\infty$ ו-$\sum _{i=1}^{\infty }\prod _{n=1}^{i}{\frac {\lambda _{n-1}}{\mu _{n}}}<\infty$.

מרחב המצבים של תהליך לידה ומוות הוא בעל התמדה ריקה אם ורק אם מתקיים $\sum _{i=1}^{\infty }\prod _{n=1}^{i}{\frac {\mu _{n}}{\lambda _{n}}}=\infty$ ו- $\sum _{i=1}^{\infty }\prod _{n=1}^{i}{\frac {\lambda _{n-1}}{\mu _{n}}}=\infty$.

כאשר מיישמים את המבחן המורחב של ברטרנד (מבחן ההמנה) ניתן לקבל את התנאים להתמדה, ארגודיות והתמדה ריקה בצורה יותר מפורשת.

עבור שלם ${\textstyle K\geq 1}$, נסמן ב-$\ln _{(K)}(x)$ את האיטרציה ה-$K$ של הלוג הטבעי, כלומר $\ln _{(1)}(x)=\ln(x)$ ולכל ${\textstyle 2\leq k\leq K}$, $\ln _{(k)}(x)=\ln _{(k-1)}(\ln(x))$. עם הסימון הזה תהליך לידה מוות הוא חולף אם קיימים$c>1$, ${\textstyle K\geq 1}$ ו-$n_{0}$ כך שלכל $n>n_{0}$ מתקיים

$${\frac {\lambda _{n}}{\mu _{n}}}\geq 1+{\frac {1}{n}}+{\frac {1}{n}}\sum _{k=1}^{K-1}{\frac {1}{\prod _{j=1}^{k}\ln _{(j)}(n)}}+{\frac {c}{n\prod _{j=1}^{K}\ln _{(j)}(n)}}$$

כאשר הסכום הריק עבור $K=1$ הוא $0$.

תהליך לידה-מוות הוא זמני אם קיימים $K\geq 1$ ו-$n_{0}$ כך שלכל $n>n_{0}$ מתקיים

${\frac {\lambda _{n}}{\mu _{n}}}\leq 1+{\frac {1}{n}}+{\frac {1}{n}}\sum _{k=1}^{K}{\frac {1}{\prod _{j=1}^{k}\ln _{(j)}(n)}}$

הגדרות מרחיבות לתהליכי לידה-מוות ותנאים מתאימים להתמדה וזמניות ניתן למצוא ב-.

הסתברויות גבוליות

אם תהליך לידה-מוות הוא ארגודי אז קיימות הסתברויות גבוליות, π$\pi _{k}=\lim _{t\to \infty }p_{k}(t),$, כאשר $p_{k}(t)$ היא ההסתברות שהתהליך יהיה במצב $k$ בזמן $t$. הגבולות קיימים, הם בלתי תלויים בערכי התחלה

$p_{k}(0)$ וניתן לחשבם באופן הבא:

$\pi _{k}=\pi _{0}\prod _{i=1}^{k}{\frac {\lambda _{i-1}}{\mu _{i}}},\quad k=1,2,\ldots ,$

$\pi _{0}={\frac {1}{1+\sum _{k=1}^{\infty }\prod _{i=1}^{k}{\frac {\lambda _{i-1}}{\mu _{i}}}}}.$

ניתן לקבל את ההסתברויות הגבוליות האלו מתוך מערכת המשוואות דיפרנציאליות

$$p_{0}^{\prime }(t)=\mu _{1}p_{1}(t)-\lambda _{0}p_{0}(t)\,$$

$$p_{k}^{\prime }(t)=\lambda _{k-1}p_{k-1}(t)+\mu _{k+1}p_{k+1}(t)-(\lambda _{k}+\mu _{k})p_{k}(t)$$

עבור $k=1,2,\ldots ,\,$.

תוך הסתמכות על $\sum _{k=0}^{\infty }p_{k}(t)=1$.

את המערכת של המשוואות הדיפרנציאליות ניתן לקבל ממערכת של משוואות הפרשים הבאה:

$P_{i,i+1}(\triangle t)=\lambda _{i}\triangle t+o(\triangle t),\quad i\geq 0,$

$P_{i,i-1}(\triangle t)=\mu _{i}\triangle t+o(\triangle t),\quad i\geq 1,$

$P_{i,i}(\triangle t)=1-(\lambda _{i}+\mu _{i})\triangle t+o(\triangle t),\quad i\geq 1.$

המערכת הזאת מתארת את הדינמיקה של התהליך בקטע זמן מאוד קצר $\Delta t$. במהלך קטע זמן קצר זה יש חשיבות לשלושה סוגים של דברים שסביר שיקרו; מוות אחד, לידה אחת או אף מוות ואף לידה. ההסתברויות של שני הראשונים הן, בקירוב טוב, ליניאריות עם $\Delta t$, לשאר האפשרויות, יש הסתברות קטנה משמעותית בהשוואה ל-$\Delta t$. אם התהליך נמצא במצב $k$, ההסתברות ללידה בודדת בקטע זמן שאורכו $\Delta t$ היא $\lambda _{k}\Delta t+o(\Delta t)$, ההסתברות למוות בודד היא $\mu _{k}\Delta t+o(\Delta t)$ וההסתברות לאף לידה ואף מוות היא $1-\lambda _{k}\Delta t-\mu _{k}\Delta t+o(\Delta t)$.

דוגמאות בתורת התורים

תהליך לידה טהור הוא תהליך לידה-מוות כאשר $\mu _{i}=0$ לכל $i\geq 0$. תהליך מוות טהור הוא תהליך לידה-מוות כאשר $\lambda _{i}=0$ לכל $i\geq 0$. מודל M/M/1 או באופן כללי מודל M/M/c המשמשים בתורת התורים, הם תהליכי לידה-מוות המתארים לקוחות בתור אינסופי.

דוגמאות בפילודינמיקה

תהליכי לידה-מוות משמשים בפילודינמיקה כהתפלגות פריורית עבור פילוגנים, שם עצים בינארים שבהם מאורעות לידה הם קודקודים פנימיים ומאורעות מוות הם קודקודי עלים. תהליכי לידה-מוות משמשים בפילודינמיקה ויראלית על מנת להבין תהליכי הדבקה וכיצד אוכלוסיית החולים משתנה במשך הזמן.

השימוש בתהליכי לידה-מוות מוכללים בפילודינמיקה הביאו חוקרים לבדוק עד כמה ניתן להעריך את קצבי הלידה והמוות מתוך הנתונים. למרות שבאופן כללי לא ניתן לשחזר את הקצבים מתוך הנתונים, המודלים שבהם משתמשים בפועל הם דווקא אלו שבהם ניתן לשחזר את הקצבים מתוך הנתונים.

תהליך לידה-מוות בילטרלי

תהליך לידה-מוות בילטרלי מוגדר באופן דומה לתהליך הרגיל עם ההבדל שמרחב המצבים $i=0,\pm 1,\pm 2,\ldots$ כולל גם את המספרים השליליים i$i=0,\pm 1,\pm 2,\ldots$ . תהליך לידה-מוות בילטרלי הוא מתמיד אם ורק אם

$\sum _{i=1}^{\infty }\prod _{n=1}^{i}{\frac {\mu _{n}}{\lambda _{n}}}=\infty \quad {\text{-ו}}\quad \sum _{i=1}^{\infty }\prod _{n=1}^{i}{\frac {\lambda _{-n}}{\mu _{-n}}}=\infty .$

ארגודיות והתמדה ריקה מתקבלות באופן דומה על ידי הרחבה מתוך תהליך לידה-מוות רגיל.

הערות שוליים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

38181135תהליך לידה-מוות