שרשרת פולימר אידיאלית

בפיזיקה, המושג שרשרת פולימר אידיאלית, מתייחס למודל פשוט לתיאור תרמודינמי של פולימרים. בדומה למושג גז אידיאלי, שהוא מודל פשוט לתיאור תרמודינמי של זורמים. במודל שרשרת הפולימר האידיאלית נניח כי לא קיימות אינטראקציות בין המונומרים המרכיבים את השרשרת מלבד הגבלות פיזיות שונות המתוארות על ידי תת-המודלים של השרשרת.

המודל מציג תיאור פשוט של פולימר כשרשרת של אובייקטים זהים בעלי אורך סופי l המתחברים זה לזה בקצותיהם בקונפורמציות זוויתיות שונות (ראה איור 1).

עקרונות המודל

N מונומרים זהים מרכיבים את הפולימר שאורכו הוא:

L=N\,l

כאשר N הוא מספר המונומרים.

גישה זו היא פשטנית ביותר, היות שהיא לא מתחשבת כלל באינטראקציות בין המונומרים המרכיבים את הפולימר. בגישה זו האנרגיה החופשית של הפולימר לא תלויה במבנה שלו.

ומכך נובע שבשיווי משקל תרמודינמי כל ההסתברות לקבל קונפיגורציית מבנה כלשהו שוות זו לזו.

נגדיר וקטור קצה-קצה ${\vec {R}}$ של שרשרת פולימרית אידיאלית ווקטורים

{\vec {r}}_{1},\ldots ,{\vec {r}}_{N}

המצביעים המשתייכים למונומרים.

נציין כי פיתוח זה מתייחס למצב בו מספר המונומרים N גדול מספיק, כך שמשפט הגבול המרכזי יתקיים.

קצוות השרשרת לא מחוברים לזה לזה לכן נקבל שערך התוחלת :

$\langle {\vec {R}}\rangle =\Sigma _{i=1}^{N}\langle {\vec {r}}_{i}\rangle ={\vec {0}}$

היות ש ${\vec {r}}_{1},\ldots ,{\vec {r}}_{N}$ בלתי תלויים זה בזה, ${\vec {R}}$ מתפלג לפי התפלגות נורמלית (או גאוסיאנית). ולכן בשלשה ממדים נקבל שהשונות תהיה:

\sigma ^{2}=\langle R_{x}^{2}\rangle -\langle R_{x}\rangle ^{2}=\langle R_{x}^{2}\rangle -0

ובפרט עבור כל מימד:

\langle R_{x}^{2}\rangle =\langle R_{y}^{2}\rangle =\langle R_{z}^{2}\rangle =N\,{\frac {l^{2}}{3}}

ומכאן נובע ש:

\langle {\vec {R^{2}}}\rangle =N\,l^{2}=L\,l~

ולכן וקטור קצה-קצה יהיה:

{\sqrt {\langle {\vec {R^{2}}}\rangle }}={\sqrt {N}}\,l={\sqrt {L\,l}}~

כמו כן, וקטור הקצה-קצה מתפלג לפי פונקציית צפיפות ההסתברות הבאה:

P({\vec {R}})=\left({\frac {3}{2\pi Nl^{2}}}\right)^{3/2}e^{-{\frac {3{\vec {R}}^{2}}{2Nl^{2}}}}

גודל נוסף, שמחושב פעמים רבות בפיזיקה של פולימרים, הוא רדיוס ההתמדה של הפולימר:

{\mathit {R}}_{G}={\frac {{\sqrt {N}}\,l}{{\sqrt {6}}\ }}

רלוונטיות המודל במציאות והכללה של המודל

פרק זה לוקה בחסר. אנא תרמו למכלול והשלימו אותו. הסיבה היא: חסר השלכות ויישומים.

על אף שהמודל הפשוט שמתואר לעיל לא מניב תוצאות מדויקות כלל עבור פולימרים מציאותיים ברמה המיקרוסקופית, הוא מתאר במידה יחסית מדויקת התנהגות פיזיקלית של פולימר בתמיסה שהמונומרים שלו מומסים בצורה אידיאלית עם הממס. במצב כזה האינטראקציות בין מונומר למונומר ובין מולקולת ממס למולקולת ממס ובין מונומר למולקולת ממס הן זהות ולכן ניתן להתייחס לאנרגיה של המערכת כקבועה. (אחת ההנחות המרכזיות של מודל זה).

אמנם, הרלוונטיות של מודל זה פוחתת משמעותית בתמיסות בהן יש חשיבות לנפח של הפולימר.

ישנם מודלים אחרים המתארים שרשרת פולימרית אידיאלית תוך כדי הזנחת אינטראקציות בין המונומרים המרכיבים אותו המנבאים תוצאות נסיוניות מדויקות יותר, הנפוץ ביותר בניהם הוא מודל התולעת (באנגלית: Worm-like Chain).

דרגות חופש של פולימר

באיור 2 (משמאל) מוצג שרטוט של פולימר המורכב משלושה מונומרים, נקודת המוצא של כל מונומר i מסומנת ב ${\vec {r_{i}}}$ .

לפי הגדרת הפולימר כל המונומרים זהים כלומר $|{\vec {r_{1}}}-{\vec {r_{2}}}|=l$ .

שתי דרגות החופש של כל מונומר הן:
$\theta$ הזווית בין שני מונומרים
ו- $\varphi$ זווית הסיבוב

תרמודינמיקה של פולימר

פונקציית החלוקה : $z=Tr(e^{-\beta H})$
האנרגיה החופשית : $F=k_{B}Tlnz=U-TS$

כדי להסתכל על התרמודינמיקה של הפולימר נגדיר שני משתנים חשובים:

${\vec {R_{N}}}$ הוא המרחק מקצה לקצה של הפולימר ומוגדר על ידי ${\vec {R_{N}}}=\sum _{i=1}^{N}{\vec {r_{i}}}$
והזווית בין מונומר i למונומר i+1 תוגדר על ידי (ראה איור 2) $cos\theta _{i,i+1}={\frac {{\vec {r_{i}}}{\vec {r_{i+1}}}}{l^{2}}}$
נזכיר כי ממוצע תרמי מוגדר ע"פ $<A>={\frac {TrAe^{-\beta H}}{Tre^{-\beta H}}}$
עבור מודל זה: ההמילטוניאן יהיה תלוי בזוויות בלבד : $H=H(\theta _{i},\varphi _{i})_{i}$ ובהתאם גם פונקציית החלוקה.

הפרמטרים האופייניים של המערכת

היחס האופייני של פלורי

אידיאליות השרשרת תבוא לידי ביטוי על ידי חוסר קורלציה (מתאם) בין זוויות שונות המופרדות על ידי מרחקים גדולים כלומר
$lim_{|i-j|\to \infty }<cos\theta _{ij}>=0$
אך שימו לב שהסכום על כל מיצועי הזוויות לא בהכרח מתאפס אלא שואף לקבוע
$C'_{i}\equiv \sum _{j=1}^{N}<cos\theta _{ij}>$
וסה"כ נקבל את "היחס האופייני של פלורי"

 $C_{n}\equiv {\frac {1}{n}}\sum _{i=1}^{n}C'_{i}$

אורך קהן

גודל בעל חשיבות נוסף במערכת הוא אורך קהן (Kuhn length). ניתן להגדירו באמצעות היחס האופייני של פלורי: $b=lC_{\infty }$ .
יש הקוראים לו האורך האפקטיבי של המערכת $l_{eff}$ ובספרים שונים הוא יכול להופיע בסימנים שונים.
למעשה, באמצעות גודל אופייני זה ניתן לתאר שרשראות מורכבות, בעלות קורלציה (נמוכה!) בין זוויות של מונומרים קרובים, כשרשרת אידיאלית פשוטה עם אורך "מונומר" אפקטיבי b.

האורך האופייני של השרשרת

במערכת ישנם שני אורכים חשובים: האורך האופייני של השרשרת $R_{0}$ ורדיוס ההתמדה $R_{G}$ , את הראשון קל לחשב משיקולים תרמודינמיים ואת השני קל למדוד בניסויי פיזור. בין שני הגדלים קיים יחס ליניארי : ${R_{G}}^{2}={\frac {1}{6}}{R_{0}}^{2}$ ,כך שע"י הצבת אחד הגדלים ניתן למצוא את השני.

רדיוס ההתמדה

באנגלית Radius of gyration, מוגדר ע"פ:
$R_{g}^{2}\equiv {\frac {1}{N}}\sum _{i=1}^{N}({\vec {r_{i}}}-{\vec {R_{cm}}})^{2}$
כאשר ${\vec {r_{i}}}$ הוא וקטור מיקום של מונומר i ו ${\vec {R_{cm}}}$ הוא וקטור מיקום מרכז המסה של הפולימר כולו.
וקטור מרכז המסה מוגדר ע"פ ${\vec {R_{cm}}}\equiv {\frac {1}{N}}\sum _{j=1}^{N}{\vec {r_{j}}}$
נכניס את הגדרת מרכז המסה להגדרת רדיוס ההתמדה ונקבל:
$R_{g}^{2}={\frac {1}{N^{2}}}\sum _{i=1}^{N}\sum _{j=1}^{N}({\vec {r_{i}}}^{2}-{\vec {r_{i}}}{\vec {r_{j}}})$
עבור שרשרת אידיאלית יש סימטריה בין ${\vec {r_{i}}},{\vec {r_{j}}}$ ולכן מותר לכתוב: ${\vec {r_{i}}}^{2}-{\vec {r_{i}}}{\vec {r_{j}}}={\vec {r_{i}}}^{2}-2{\vec {r_{i}}}{\vec {r_{j}}}+{\vec {r_{j}}}^{2}=({\vec {r_{i}}}-{\vec {r_{j}}})^{2}$ .
רדיוס ההתמדה הממוצע:
$<R_{g}^{2}>={\frac {1}{N^{2}}}\sum _{i=1}^{N}\sum _{j=1}^{N}<({\vec {r_{i}}}-{\vec {r_{j}}})^{2}>$
בגבול הרצף : $N\to \infty ,l\to 0;Nl=const$ הסכומים הופכים לאינטגרלים $\sum _{i=1}^{N}\to \int _{0}^{N}du,\sum _{j=i}^{N}\to \int _{u}^{N}dv$

ואז אפשר לחשב את רדיוסי ההתמדה ע"פ הגאומטריה של הפולימר:

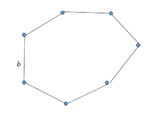
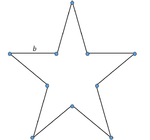
סוג השרשרת	ליניארית	טבעתית	f-arm star	H-polymer
תיאור גאומטרי של הפולימר (ע"פ מונומר באורך קהן b)			f = 5
$<R_{g}^{2}>$ (ממוצע רדיוס ההתמדה בריבוע)	${\frac {Nb^{2}}{6}}$	${\frac {Nb^{2}}{12}}$	${\frac {(N/f)b^{2}}{6}}(3-{\frac {2}{f}})$	${\frac {Nb^{2}}{6}}{\frac {89}{625}}$

מציאת האורך האופייני של השרשרת $R_{0}$ משיקולים תרמודינמיים

משיקולי סימטריה ברור כי הממוצע $<{\vec {R_{N}}}>=0$ . זאת מכיוון שאנו סוכמים על כל הקונפיגורציות האפשריות בבעיה ומאחר ו- ${\vec {R_{N}}}$ הוא וקטור, נוכל למצוא עבור כל ${\vec {r_{i}}}$ וקטור השווה לו בגודלו והפוך בכיוונו ${\vec {-r_{i}}}$ .

אך השונות לא מתאפסת:
$<{\vec {R_{N}^{2}}}>=<R_{N}R_{N}>=<\sum _{i}{\vec {r_{i}}}\sum _{j}{\vec {r_{j}}}>=\sum _{i,j}^{N}<r_{i}r_{j}>=\sum _{i,j=1}^{N}l^{2}<cos\theta _{ij}>$

ובגבול $N>>1$ נקבל: $<R^{2}>\cong C_{\infty }Nl^{2}$

מאחר שהממוצע על ${\vec {R_{N}}}$ מתאפס, השונות : $\sigma _{R_{N}}^{2}=<R_{N}^{2}>-<R_{N}>^{2}=<R_{N}^{2}>\neq 0$
נגדיר את האורך האופייני של השרשרת כסטיית התקן : $R_{0}={\sqrt {<R_{N}^{2}>}}$

מודלים לתיאור שרשרת פולימר אידיאלית

במודלים הבאים נחשב את $R_{0}$ תחת מגבלות שונות על הזוויות $\theta ,\varphi$ בין המונומרים.

שרשרת חופשית :Freely Joint Chain

במודל זה נניח כי אין הגבלות על בחירת הזוויות לאורך השרשרת.
$\theta$ מתפלגת אחיד (התפלגות אחידה) בין 0 ל- $2\pi$ : $\theta _{i}=\left\{0,2\pi \right\}$
$\varphi$ מתפלגת אחיד (התפלגות אחידה) בין $-\pi$ ל- $\pi$ : $\varphi _{i}=\left\{-\pi ,\pi \right\}$

ולכן : $<r_{i}r_{j}>=l^{2}<cos\theta _{ij}>=\delta _{ij}$
כאשר $\delta _{ij}={\begin{cases}0,&{\text{if }}i\neq j\\1,&{\text{if }}i=j\end{cases}}$ היא הדלתא של קרוניקר.
כלומר היחס האופייני של פלורי הוא: $C_{\infty }=1$ , ואורך קהן הוא: $b=l$
והאורך קצה-קצה האופייני של השרשרת :

$R_{0}={\sqrt {<R_{N}^{2}>}}=l{\sqrt {N}}$

שרשרת מסתובבת חופשית :Freely Rotating Chain

במודל זה נניח כי אחת הזוויות קבועה:
$\theta _{i}=\theta =const$
$\varphi$ מתפלגת אחיד בין $-\pi$ ל $\pi$ : $\varphi _{i}=\left\{-\pi ,\pi \right\}$

נחשב את :

שכנים קרובים מדרגה ראשונה: $<r_{i}r_{i+1}>=l^{2}<cos\theta _{i}>=l^{2}<cos\theta >$
שכנים קרובים מדרגה שנייה: $<r_{i}r_{i+2}>=l^{2}<cos\theta _{i}cos\theta _{i+1}>=l^{2}<cos^{2}\theta >$
מכאן נסיק כי עבור i,j כלליים נקבל : $<r_{i}r_{j}>=l^{2}<cos^{|i-j|}\theta >$

כלומר : $R_{0}^{2}=\sum _{i=1}^{N}\sum _{j=1}^{N}<{\vec {r_{i}}}{\vec {r_{j}}}>=\sum _{i=1}^{N}<r_{i}^{2}>+l^{2}\sum _{i=1}^{N}[\sum _{j=1}^{i-1}(cos\theta )^{i-j}+\sum _{j=i+1}^{N}(cos\theta )^{j-i}]$

נשים לב כי : $\sum _{i=1}^{N}<r_{i}^{2}>=Nl^{2}$
$\sum _{j=1}^{i-1}$ הוא פשוט סכימה על $j<i$
$\sum _{j=i+1}^{N}$ הוא פשוט סכימה על $j>i$

נחליף למשתנה סכימה קל יותר : $k=i-j$ ונקבל:
$R_{0}^{2}=Nl^{2}+l^{2}\sum _{i=1}^{N}[\sum _{k=1}^{N}(cos\theta )^{k}+\sum _{k=1}^{N-i}(cos\theta )^{k}]$
תוצאת הסכום עד N כללי: $\sum _{k=1}^{N}={\frac {cos\theta }{1-cos\theta }}[1-cos^{N}\theta ]$
ולכן נקבל כי
$R_{0}^{2}=Nl^{2}+l^{2}\sum _{i=1}^{N}{\frac {cos\theta }{1-cos\theta }}[2-cos^{i-1}\theta -cos^{N-i}\theta ]$

בשונה מהשרשרת החופשית, בשרשרת המסתובבת קיימת קורלציה בין זוויות מונומרים שכנים בשרשרת :

${\frac {r_{i}r_{j}}{l^{2}}}=(cos\theta )^{|j-i|}=exp[|j-i|ln(cos\theta )]$
אם נגדיר את אורך הקורלציה : $s_{p}=-{\frac {1}{ln(cos\theta )}}$
נקבל כי אורך הקורלציה יורד אקספוננציאלית עם המרחק בין המונומרים.

ובגבול $N>>1$ וזוויות גדולות נקבל:
אורך קורלציה : $s_{p}\cong 1$ , היחס האופייני של פלורי $C_{\infty }={\frac {1+cos\theta }{1-cos\theta }}\cong 2$ , ואורך קהן $b=l{\frac {1+cos\theta }{1-cos\theta }}\cong 2l$

והאורך קצה-קצה האופייני של השרשרת :  $R_{0}^{2}=Nl^{2}{\frac {1+cos\theta }{1-cos\theta }}$

בגבול הרציפות כאשר $N\rightarrow \infty ,\theta \rightarrow 0$ :

$s_{p}\thickapprox {\frac {2}{\theta ^{2}}}\rightarrow \infty$

נגדיר את הגודל המקסימלי שהפולימר יכול לקבל: $R_{max}=NLcos({\frac {\theta }{2}})\thickapprox Nl$

לכן נדרוש $N\rightarrow \infty ,l\rightarrow 0$ , כך ש $Nl=const$ . גבול זה נקרא שרשרת כמו-תולעת (באנגלית: Worm-like chain).

ניזכר כי: $R_{0}^{2}=\sum _{i=1}^{N}\sum _{j=1}^{N}<{\vec {r_{i}}}{\vec {r_{j}}}>=\sum _{i=1}^{N}\sum _{j=1}^{N}(cos(\theta ))^{\left\vert i-j\right\vert }=l^{2}\sum _{i=1}^{N}\sum _{j=1}^{N}exp(-{\frac {\left\vert i-j\right\vert }{s_{p}}})$

נקבל לאחר מעבר לגבול הרצף: $R_{0}^{2}=l^{2}\textstyle \int _{0}^{R_{max}}\displaystyle {\frac {du}{l}}\textstyle \int _{0}^{R_{max}}\displaystyle {\frac {dv}{l}}exp(-{\frac {\left\vert u-v\right\vert }{ls_{p}}})$

ולבסוף נקבל: $R_{0}^{2}=2ls_{p}R_{max}-2(ls_{p})^{2}[1-exp(-{\frac {R_{max}}{ls_{p}}})]$

נקבל שני מקרים: (בכל מקרה $R_{max}\gg l$ )

המקרה הקשיח: $ls_{p}\gg R_{max}\gg l$ נפתח את האקספוננט לטור ונקבל $R_{0}\thickapprox R_{max}=lN$
המקרה הגמיש: $R_{max}\gg ls_{p}\gg l$ נקבל שהאקספוננט שואף לאפס, ולכן $R_{0}^{2}\thickapprox 2ls_{p}R_{max}-2(ls_{p})^{2}\thickapprox 2ls_{p}R_{max}$ לכן מקבלים $R_{0}={\sqrt {lN2ls_{p}}}={\sqrt {Ll_{eff}}}$ , כלומר שרשרת אידיאלית עם $l_{eff}=2ls_{p}$

שרשרת מסתובבת מוגבלת: Hindered Rotation

במודל זה נניח כי אחת הזווית קבועה:
$\theta _{i}=\theta =const$
$\varphi$ מתפלגת ע"פ פוטנציאל $U(\varphi _{i})$ בין $-\pi$ ל $\pi$ , וההסתברות לקבלת זווית מסוימת מתפלגת ע"פ התפלגות בולצמן
$<cos\varphi >={\frac {\int _{0}^{2\pi }(cos\varphi )exp(-U(\varphi _{i})/k_{B}T)d\varphi }{\int _{0}^{2\pi }exp(-U(\varphi _{i})/k_{B}T)d\varphi }}$

ובגבול $N>>1$ נקבל פשוט
אורך קורלציה : $s_{p}\cong {\frac {1+<cos\varphi >}{1-<cos\varphi >}}$ , היחס האופייני של פלורי $C_{\infty }={\frac {1+cos\theta }{1-cos\theta }}{\frac {1+<cos\varphi >}{1-<cos\varphi >}}$ , ואורך קהן $b=l{\frac {1+cos\theta }{1-cos\theta }}{\frac {1+<cos\varphi >}{1-<cos\varphi >}}$

והאורך קצה-קצה האופייני של השרשרת :  $R_{0}^{2}=Nl^{2}{\frac {1+cos\theta }{1-cos\theta }}{\frac {1+<cos\varphi >}{1-<cos\varphi >}}$

שרשרת מסתובבת איזומרית Rotational Isomeric State

איזומר היא מולקולה שבה סידור האטומים יכול להתקיים בצורות שונות. מודל השרשרת המסתובבת האיזומרית מתייחס לקבוצת איזומרים מוגדרת:

בעלי שלושה מצבים
בין המצבים ניתן לעבור באמצעות סיבוב סביב קשר קוולנטי בודד בין שני אטומים.
נניח מחסום פוטנציאל גבוה, כלומר $\Delta E>>k_{B}T$ . כאשר $\Delta E$ הוא פער האנרגיה בין המצבים.

ההנחות הזוויתיות של המודל מסתכמות ל:
$\theta _{i}=\theta =const$
$\varphi$ מתפלג אחיד בין מספר מצומצם של זוויות בדידות.

מספר המצבים של המערכת נקבע ע"פ מספר הקשרים הראשיים בשרשרת, כלומר עבור $n$ קשרים ראשיים יהיו $n-2$ זוויות סיבוב ולכן סה"כ יהיו $3^{n-2}$ מצבי סיבוב איזומריים.

לדוגמה ל n-pentane יש 4 קשרים ראשיים ולכן $3^{4-2}=9$ מצבי סיבוב.

מאחר שמספר המצבים לא אחיד לכל הפולימרים שניתן לתאר באמצעות מודל זה, התפלגות ההסתברות של כל זווית לא נקבעת במודל. לכן לא קיים חישוב כללי של $C_{\infty }$ או של אורך קהן. אפשר לראות כי דרגת המורכבות של מודל זה גבוהה בהרבה משאר המודלים ועל כן הוא מצליח לשקף את המציאות בצורה הטובה ביותר. ואכן הוא נחשב למודל המוצלח ביותר עבור שרשרת אידיאלית.

סיכום והשוואה בין מודלי שרשרת הפולימר האידיאלית

פרמטר	שרשרת חופשית	שרשרת מסתובבת	מסתובבת מוגבלת	מסתובבת איזומרית
$\theta$ - הזווית בין שני מונומרים	התפלגות אחידה	קבוע	קבוע	קבוע
$\varphi$ - זווית הסיבוב	התפלגות אחידה	התפלגות אחידה	ע"פ פוטנציאל $U(\varphi )$	בדיד: $3^{n-2}$ מצבי סיבוב
$l_{eff}$ - אורך קהן (b)	$l$	$l{\frac {1+cos\theta }{1-cos\theta }}$	$l{\frac {1+cos\theta }{1-cos\theta }}{\frac {1+<cos\varphi >}{1-<cos\varphi >}}$	אין חישוב כללי
$C_{\infty }$ - היחס האופייני של פלורי	1	${\frac {1+cos\theta }{1-cos\theta }}$	${\frac {1+cos\theta }{1-cos\theta }}{\frac {1+<cos\varphi >}{1-<cos\varphi >}}$	אין חישוב כללי
$R_{0}$ - אורך קצה-קצה האופייני של השרשרת	$l{\sqrt {N}}$	${\sqrt {Nll_{eff}}}$	${\sqrt {Nll_{eff}}}$	אין חישוב כללי