העתקת מביוס

באנליזה מרוכבת, העתקת מביוס או טרנספורמציית מביוס היא פונקציה מרוכבת מהצורה $T(z)={\frac {az+b}{cz+d}}$ כאשר $\ a,b,c,d$ הם מקדמים מרוכבים כך ש $\ ad-bc\neq 0$.

העתקות מביוס קרויות על שם המתמטיקאי הגרמני אוגוסט פרדיננד מביוס.

סקירה כללית ותכונות

כל העתקת מביוס היא העתקה רציפה, חד חד ערכית ועל מהמישור המרוכב המורחב לעצמו. הרחבת המישור המרוכב נעשית על ידי הוספת נקודה באינסוף (המישור המורחב נקרא ספירת רימן ומסומן ${\widehat {\mathbb {C} }}=\mathbb {C} \cup \{\infty \}$; הטופולוגיה שלו מתקבלת מן הקומפקטיפיקציה של אלכסנדרוף). העתקות מביוס הן העתקות מרומורפיות בכל $\mathbb {C}$, והולומורפיות בכל ספירת רימן. הרציפות והאנליטיות באינסוף מושגות על ידי הגדרת הפונקציה בצורה האינטואיטיבית $T\left({\frac {-d}{c}}\right)=\infty ,T(\infty )={\frac {a}{c}}$. במקרה שבו $\ c=0$ הפונקציה היא פשוט ליניארית ומוגדרת על כל ${\widehat {\mathbb {C} }}$ כאשר $\ T(\infty )=\infty$.

• הרכבה של העתקות מביוס היא גם העתקת מביוס, ולכן העתקות מביוס מהוות חבורה, וחבורת העתקות מביוס מהוות את חבורת האוטומורפיזמים של ספירת רימן, ומסומנת לעיתים ${\mbox{Aut}}({\widehat {\mathbb {C} }})$. במינוח של גאומטריה דיפרנציאלית, נאמר כי העתקות מביוס הן כל הדיפאומורפיזמים של ספירת רימן לעצמה. ישנן תתי חבורות של העתקות מביוס המהוות את האוטומורפיזמים של משטחי רימן אחרים, כמו המישור המרוכב או המישור ההיפרבולי, ועל כן העתקות מביוס מהוות חלק חשוב בתאוריה של משטחי רימן.

• כל העתקת מביוס היא הולומורפית, ולכן קונפורמית, כלומר שומרת זוויות.

• העתקת מביוס מעתיקה מעגלים וישרים ב $\mathbb {C}$ למעגלים וישרים, אך לא בהכרח מעתיקה מעגל למעגל וישר לישר. ניתן לנסח תכונה זו בצורה פשוטה ואלגנטית יותר, אם מרחיבים את הדיון לספירת רימן כולה(${\widehat {\mathbb {C} }}$). נשים לב כי גם מעגלים וגם ישרים ב $\mathbb {C}$ מתאימים למעגלים ב ${\widehat {\mathbb {C} }}$, כאשר ישרים ב $\mathbb {C}$ מתאימים למעגלים העוברים דרך הקוטב הצפוני. לכן, מעל ספירת רימן ניתן לומר בפשטות כי העתקת מביוס מעתיקה מעגלים למעגלים.

• העתקת מביוס שומרת על היחס הכפול. היחס הכפול של 4 נקודות (שונות) ב $\mathbb {C}$ מוגדר כך $\ [z_{1},z_{2},z_{3},z_{4}]={\frac {(z_{1}-z_{3})(z_{2}-z_{4})}{(z_{1}-z_{4})(z_{2}-z_{3})}}$, ולכל העתקת מביוס מתקיים $\ [z_{1},z_{2},z_{3},z_{4}]=[T(z_{1}),T(z_{2}),T(z_{3}),T(z_{4})]$.

• כל העתקת מביוס נקבעת על ידי ערכיה על שלוש נקודות. בפרט העתקת מביוס שיש לה שלוש נקודות שבת חייבת להיות העתקת הזהות. לכל העתקת מביוס שאינה הזהות יש לפחות נקודת שבת אחת, ולכל היותר שתיים.

נקודות שבת

לכל העתקת מביוס השונה מהעתקת הזהות יש בדיוק שתי נקודות שבת $\gamma _{1},\gamma _{2}$ במישור המרוכב המורחב. נקודות שבת אלו נספרות בהתאם לריבוי האלגברי שלהן, ומבחינה גאומטרית הן יכולות להתלכד לכדי נקודת שבת אחת; העתקות כאלו נקראות העתקות פרבוליות. כל אחת מהנקודות הללו, ולעיתים אף שתיהן, עשויה להיות הנקודה באינסוף.

קביעת נקודות השבת

נקודות השבת של הטרנספורמציה

$f(z)={\frac {az+b}{cz+d}}$

נקבעות על ידי פתרון משוואת נקודת השבת f(γ) = γ. בעבור c ≠ 0, למשוואה זו יש שני שורשים המתקבלים מפתרון המשוואה הריבועית

$c\gamma ^{2}-(a-d)\gamma -b=0\ ,$

השורשים הם:

$\gamma _{1,2}={\frac {(a-d)\pm {\sqrt {(a-d)^{2}+4bc}}}{2c}}={\frac {(a-d)\pm {\sqrt {\Delta }}}{2c}}$

ולמשוואה הריבועית יש דיסקרימיננטה

$\Delta =(\operatorname {tr} {\mathfrak {H}})^{2}-4\operatorname {det} {\mathfrak {H}}=(a+d)^{2}-4(ad-bc)$.

להעתקות פרבוליות יש נקודות שבת מתלכדות אודות לדיסקרימיננטה אפס. בעבור c שונה מאפס ודיסקרימיננטה שונה מאפס ההעתקה תיקרא אליפטית או היפרבולית.

כאשר c = 0 המשוואה הריבועית מתנוונת לכדי משוואה ליניארית וההעתקה היא ליניארית. זה תואם למצב שבו אחת מנקודות השבת היא הנקודה באינסוף. כאשר a ≠ d נקודת השבת השנייה היא סופית וניתנת בנוסחה

$\gamma =-{\frac {b}{a-d}}.$

במקרה זה ההעתקה פועלת במסגרת המישור המרוכב כהרכבה של הזזה (translation), סיבוב (כאשר ל-$\alpha =a/d$ יש חלק מדומה) ומתיחה/כיווץ (dilation):

$z\mapsto \alpha z+\beta .\,$

אם c = 0 ו-a = d, אז שתי נקודות השבת הן באינסוף, והעתקת מביוס תואמת להזזה טהורה:

$z\mapsto z+\beta .$

העתקות מביוס כתנועות של הספירה של רימן

המישור המרוכב וספירת רימן שמעליו.

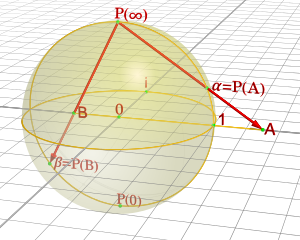
את המישור המרוכב המורחב ניתן לזהות כהטלה הסטריאוגרפית של הספירה של רימן; הנקודה "באינסוף" היא למעשה ההטלה של הנקודה דרכה מתבצעת ההטלה הסטריאוגרפית, על המישור המרוכב. תחת נקודת המבט הזו, העתקות מביוס ניתנות לזיהוי כתנועות של הספירה של רימן. המקרה של העתקת מביוס המייצג הזזה תואם לתנועה קווית (הזזה גם כן) של ספירת רימן. בנוסף, הספירה של רימן עשויה להסתובב ולשנות את האוריינטציה שלה במרחב; אחד המשפטים המרכזיים בנוגע לסיווג העתקות מביוס קובע שכל העתקות מביוס התואמות לסיבוב טהור של ספירת רימן הן מהצורה:

$f(z)={\frac {\alpha z+\beta }{-{\bar {\beta }}z+{\bar {\alpha }}}}={\frac {(a+bi)z+(c+di)}{-(c-di)z+(a-bi)}}$

כאשר $|\alpha |^{2}+|\beta |^{2}=a^{2}+b^{2}+c^{2}+d^{2}=1$. זוהי למעשה העתקת מביוס אוניטרית. על פי משפט הסיבובים של אוילר, הרכבה של שני סיבובים תלת-ממדיים היא בעצמה סיבוב תלת-ממדי, ולכן האוסף של העתקות מביוס אוניטריות מהווה תת-חבורה של החבורה הכללית של העתקות מביוס.

העתקות מביוס מסוג מתיחה/כיווץ (דהיינו $f(z)=kz$ כאשר k ממשי ושונה מ-1) ניתנות לפירוש כהגדלה או כיווץ של ספירת רימן - כך שהמרחק מהראשית של ההיטלים של נקודות עליה מוגדל באותו יחס - ולא כתנועות שלה, ולפיכך אינן רלוונטיות לחלק זה.

זיהוי הסיבוב המתאים להעתקת מביוס אוניטרית נתונה

נקודת המבט הגאומטרית מאפשרת לתת הסבר אינטואיטיבי לנקודות השבת של העתקת מביוס, במקרה של סיבוב טהור; אלו הן בדיוק התמונות של קטבי הסיבוב המתאים של ספירת רימן (הנקודות בהן חותך ציר הסיבוב את הספירה), תחת פעולת ההטלה הסטריאוגרפית. בנוסף, שורש אחד של המשוואה הריבועית (משוואת נקודת השבת) מתקבל מאחר על ידי הנגדה של האינוורסיה של השורש השני; הווה אומר:

$\gamma _{2}=-{\frac {1}{\bar {\gamma _{1}}}}$,

והקדם-תמונה של הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma_2} היא הנקודה האנטיפודית של הקדם-תמונה של הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma_1} על ספירת רימן.

את הסיבוב המתאים להעתקת מביוס אוניטרית נתונה ניתן לתאר באמצעות הצגה קווטרניונית:

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle q = cos(\epsilon/2) + (\eta_1 i + \eta_2 j +\eta_3 k)sin(\epsilon/2)} ,

כאשר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{\eta} = (\eta_1,\eta_2,\eta_3)} הוא וקטור יחידה המייצג את ציר הסיבוב של ספירת רימן (ראו גם קווטרניונים וסיבובים מרחביים), ו-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon} היא זווית הסיבוב מסביב לציר הזה. כדי למצוא את הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon} , נעזר במשפט החשוב הבא:

טענה: הנגזרת המרוכבת של העתקת מביוס אוניטרית הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(z)} באחת מנקודות השבת מקיימת:

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle f'(\gamma_1) = e^{i\epsilon}} .

הוכחה: נסמן את הפונקציה ההפוכה להטלה הסטריאוגרפית ב-$P(z)=S^{-1}(z)$, ונוכיח תחילה ש-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle |f'(\gamma_1)| = 1} . בסביבה כדורית אינפיניטסימלית של הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(\gamma_1)} שתי הקדם-תמונות של הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle z_1+dz} ו-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(z_1+dz)} נמצאות במרחק שווה מאותו קוטב (הן באותו "קו רוחב") - ומכיוון שהן כמעט באותה נקודה (המרחק ביניהן שואף לאפס) פעולת ההטלה הסטריאוגרפית תמתח מרחקים זהים אלו באותה מידה - ולכן גודל השינוי האינפיניטסימלי ב-z מתורגם לשינוי בעל גודל זהה של (f(z, או במילים אחרות הערך המוחלט של הנגזרת המרוכבת בנקודת השבת הוא 1. כעת נוכיח ש-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle f'(\gamma_1) = e^{i\epsilon}} . ההסבר לעובדה זו נעוץ בכך שההטלה הסטריאוגרפית, כמו העתקת מביוס, היא קונפורמית (משמרת זוויות בין עקומים). נסתכל על שני הקטעים הבאים במישור המרוכב: הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle [\gamma_1,\gamma_1+dz]} ו-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle [\gamma_1,f(\gamma_1+dz)]} . שני קטעים אלו יוצרים ביניהם זווית $\epsilon$, וזאת משום שהם מהווים הטלה של משולש כדורי אשר קודקוד אחד שלו נמצא בקוטב של הסיבוב המגדיר את העתקת מביוס, קודקוד שני ב-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(\gamma_1+dz)} וקודקוד שלישי ב-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(f(\gamma_1+dz))} . הזווית הפולרית (הזווית בקודקוד הקוטבי) של המשולש הכדורי הזה היא לפי הגדרה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon} , ולכן מתכונת הקונפורמיות נובע שגם הזווית בין הקטעים היא הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon} , ופירוש הדבר הוא ש-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle f'(\gamma_1) = e^{i\epsilon}} . מ.ש.ל

כדי להמשיך בפיתוח, תחילה נמצא את הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma_1} :

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle -(c-di)\gamma^2-2bi\gamma-(c+di)=0\implies \gamma_{1,2} = \frac{-d + ci}{c^2+d^2} (-b\pm \sqrt{1-a^2}) }

הנגזרת של העתקת מביוס בנקודת השבת נותנת:

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{i\epsilon} = f'(\gamma_1) = \frac{2a+\sqrt{(2bi)^2-4(c^2+d^2)}}{2a-\sqrt{(2bi)^2-4(c^2+d^2)}} = \frac{2a+2i\sqrt{1-a^2}}{2a-2i\sqrt{1-a^2}} = \frac{a+i\sqrt{1-a^2}}{a-i\sqrt{1-a^2}}}

ולפי זהויות טריגונומטריות של חצי-זווית פירוש הדבר הוא ש-: הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle cos(\epsilon/2) = a} , ולכן החלק הממשי של הקווטרניון המייצג של הסיבוב הוא הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle a} . בנוסף לכך, הנורמה של הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma_1} שווה לפי תכונות ההטלה הסטריאוגרפית ל-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle cot(\theta/2)} כאשר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} היא זווית הזנית של הקדם-תמונה של הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma_1} על ספירת רימן (זווית הזנית היא קואורדינטה כדורית). לפיכך נקבל:

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle cot(\theta/2) =|\gamma_1| = \frac{-b+\sqrt{1-a^2}}{\sqrt{c^2+d^2}} \implies cos\theta = \frac{cot^2(\theta/2)-1}{cot^2(\theta/2)+1} = -\frac{b}{\sqrt{1-a^2}}}

הגודל הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle cos\theta} הוא לא אחר מאשר הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta_z} , ונזהה את ציר z עם הקווטרניון היסודי k. בדומה לכך נקבל, שמכיוון שמתקיים הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\eta_{y}}{\eta_{x}} = -\frac{d}{c}} , וכמו כן הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta_x^2 + \eta_y^2 + \eta_z^2 = 1} , ש-:

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat{\eta} = (\frac{c}{\sqrt{1-a^2}},\frac{-d}{\sqrt{1-a^2}},\frac{-b}{\sqrt{1-a^2}})}

וזה משלים את מציאת החלק הווקטורי של הקווטרניון המייצג. לסיכום, בהצגה קווטרניונית נקבל:

הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle q = cos(\epsilon/2)+(\eta_{x}i+\eta_{y}j+\eta_{z}k)sin(\epsilon/2) = a+(\eta_{x}i+\eta_{y}j+\eta_{z}k)\sqrt{1-a^2} = a + ci - dj - bk}

כאשר במעבר האחרון זיהינו את ציר j עם הישר הממשי ואת ציר i עם הישר המדומה.

העתקות מביוס כמטריצות

אם נרכיב את ההעתקה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_1(z)=\frac{az+b}{cz+d}} עם ההעתקה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_2(z)=\frac{a'z+b'}{c'z+d'}} , תתקבל העתקה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle T_3(z)=T_1 \circ T_2=\frac{(a'a+c'b)z+(b'a+d'b)}{(a'c+c'd)z+(b'c+d'd)}} . ניתן לזהות קשר הדוק עם כפל המטריצות הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{pmatrix} a & b\\ c & d \end{pmatrix} \begin{pmatrix} a' & b' \\ c' & d' \end{pmatrix}=\begin{pmatrix} a'a+c'b & b'a+d'b\\ a'c+c'd & b'c+d'd \end{pmatrix}} .

נשים לב גם כי כפל בסקלר של כל המקדמים אינו משנה את ההעתקה - הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{az+b}{cz+d}=\frac{\lambda az+\lambda b}{\lambda cz+\lambda d}} . בנוסף, הדרישה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ ad-bc \ne 0} היא בדיוק הדרישה שהמטריצה תהיה הפיכה. לכן, ניתן לזהות העתקות עם העתקות ליניאריות מ הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{C}^2} ל הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbb{C}^2} , עד כדי כפל במטריצה סקלרית. כלומר, הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \mbox{Aut}(\widehat {\mathbb{C}}) \cong \operatorname{PGL}_2(\mathbb{C})} , (כאשר $\ \operatorname {PGL_{2}}$ היא חבורת המטריצות ההפיכות, מודולו המטריצות הסקלריות).

קישורים חיצוניים

מדיה וקבצים בנושא העתקת מביוס בוויקישיתוף

• העתקת מביוס, באתר MathWorld (באנגלית)   

הערות שוליים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

29094079העתקת מביוס