שדה חשמלי

שדה חשמלי היא תכונה פיזיקלית של המרחב המקיף מטען חשמלי (או של אזור בו יש שדה מגנטי המשתנה בזמן). שדה מפעיל כוח על גופים הטעונים חשמלית. רעיון השדה החשמלי הוצע על ידי מייקל פאראדיי.

השדה החשמלי הוא וקטור. במערכת היחידות הבינלאומית הוא נמדד ביחידות של ניוטון לקולון $\left[{\frac {N}{C}}\right]$, או באופן שקול, ביחידות של וולט למטר $\left[{\frac {V}{m}}\right]$.

הגדרת השדה החשמלי

באלקטרוסטטיקה (כאשר כל המטענים אליהם מתייחסים נמצאים במנוחה), כיוון השדה עבור נקודה כלשהי במרחב מוגדר על ידי כיוון הכוח החשמלי המופעל על מטען בוחן חיובי המונח בנקודה זו. עוצמת השדה מוגדרת על ידי היחס בין גודלו של הכוח החשמלי המופעל על המטען המונח בנקודה זו לבין גודלו של המטען בנקודה. הרעיון הוא לבדוק את השפעת כלל המטענים במרחב על מטען הבוחן, באופן כזה שלמטען הבוחן אין השפעה על השדה הנמדד.

השדה החשמלי מוגדר ככוח על מטען הבוחן ליחידת מטען בוחן: ${\vec {E}}={\frac {\vec {F}}{q}}$ כאשר:

${\vec {F}}$ הוא הכוח החשמלי הנתון על ידי חוק קולון.

$q$ הוא גודל מטען הבוחן.

המשוואה לעיל תקפה רק כאשר כל המטענים במנוחה. במקרה הכללי של מטענים נעים המשוואה הנ"ל הופכת למשוואה של כוח לורנץ.

תיאור גרפי של השדה החשמלי

תיאור גרפי של שדה חשמלי המקיף מטען חיובי (אדום) ומטען שלילי (ירוק) (לתמונה גדולה יותר).

קיימות מספר דרכים לתיאור גרפי של שדה חשמלי. שדה חשמלי סטטי יתואר בדרך כלל על ידי קווי שדה. קווי שדה הם קווים שכיוונם מתאר את כיוון תנועתו של מטען חיובי מנקודה מסוימת, ואורכם מתאר את גודל הכוח שיפעל על אותו מטען. צפיפותם היחסית של קווי השדה בנקודה מסוימת, מלמדים על עוצמת השדה החשמלי באותה נקודה: ככל שקווי השדה צפופים יותר כך עוצמת השדה גבוהה יותר, ולהפך. שדה חשמלי חייב להיות סימטרי.

השדה החשמלי הנוצר על ידי מטען חיובי ידחה מטען בוחן חיובי, ולכן קווי השדה סביבו יתוארו על ידי חיצים הפונים החוצה. באופן דומה השדה הנוצר על ידי מטען שלילי ימשוך מטען בוחן חיובי, ולכן קווי השדה סביבו יתוארו על ידי חיצים הפונים פנימה.

שדה חשמלי של מטען נקודתי

שדה חשמלי של מטען נקודתי

שדה חשמלי בין שני מטענים נקודתיים מנוגדים

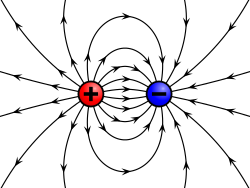
כל מקור טעון חשמלית יוצר שדה חשמלי במרחב. עוצמת השדה בכל נקודה תלויה בהתפלגות המטען על המקור, ולכן קשה לחשב אותה למקרה כללי. המקרה הבסיסי ביותר הוא כאשר המקור הוא חסר ממדים, כלומר הוא נקודה. לכן מנתחים מרחב ריק שבו נמצא רק מטען אחד: חלקיק נקודתי.

הפיזיקאי שארל-אוגוסטן דה קולון היה הראשון שגילה את הקשר בין גודלו של מטען $\ q$ שמונח בשדה חשמלי שיוצר מטען אחר $\ Q$, לבין גודל הכוח החשמלי שמופעל עליו, $\ F$. הנוסחה המתארת את הכוח הזה נקראה על שמו – חוק קולון – ולפיה הכוח החשמלי שיפעל על מטען כלשהו שיונח בשדה יהיה מכפלה של גודל המטען בגודל המטען שיצר את השדה, מחולק בריבוע המרחק מהמטען. במילים אחרות, השדה החשמלי במרחק $\ r$ ממקור חשמלי נקודתי יחיד שמטענו $\ Q$ הוא $\ E={\frac {kQ}{r^{2}}}$, והכוח שמפעיל השדה על המטען $\ q$ נתון על ידי $\ \ F=qE={\frac {kqQ}{r^{2}}}$.

כיוונו של הכוח הוא רדיאלי, לכוון המטען שמחולל את השדה (אם המטענים הם מנוגדים, ואז הוא כוח משיכה) או החוצה ממנו (אם המטענים הם שווי-סימן, ואז הוא כוח דחייה). נוח יותר לעבוד עם וקטורים, כדי לטפל בצורה נוחה יותר בכיווני הכוחות. מסמנים ב-$\ {\hat {r}}$ וקטור יחידה בכיוון מ-$\ Q$ אל $\ q$. אם המטען $\ Q$ אינו נמצא בראשית הצירים אלא במיקום שרירותי כלשהו $\ {\vec {R}}$, וקטור היחידה הוא $\ {\hat {r}}={\frac {{\vec {r}}-{\vec {R}}}{|{\vec {r}}-{\vec {R}}|}}$ (כיוונו הוא ככיוון וקטור ההפרש בין וקטורי המקום והוא מחולק בגודלו של וקטור ההפרש כדי לקבל וקטור שגודלו יחידה).

לכן הכוח הפועל בין שני מטענים נקודתיים הנמצאים בנקודות $\ {\vec {R}}\,\ {\vec {r}}$ בהתאמה הוא $\ {\vec {F}}=q{\vec {E}}=qQk{\frac {{\vec {r}}-{\vec {R}}}{|{\vec {r}}-{\vec {R}}|^{3}}}$

הקבוע $\ k$ הוא קבוע קולון במערכת היחידות SI. במקומו רושמים לפעמים ${\frac {1}{4\pi \epsilon _{0}}}$ (‏$\ \epsilon _{0}$ הוא המקדם הדיאלקטרי של הריק, או פֶּרְמיטיביות הריק). כאן $\ k=1/(4\pi \epsilon _{0})\approx 9\times 10^{9}\ [{\frac {{\mbox{N}}\cdot {\mbox{m}}^{2}}{{\mbox{Coul}}^{2}}}]$. ביחידות cgs, ערכו של k הוא 1 משום שמודדים את המטען ביחידות esu. ביחידות אלה חוק קולון הוא מהצורה: ${\vec {E}}={\frac {Q}{r^{2}}}{\hat {r}}={\frac {Q}{r^{3}}}{\vec {r}}$ זוהי נוסחה וקטורית שמשמעותה היא שגודל השדה הוא $E={\frac {kQ}{r^{2}}}$, וכיוונו הוא ככיוון הקו המחבר את הנקודה שבה בודקים את השדה עם הנקודה בה נמצא המטען היוצר את השדה. הסימן החיובי של הנוסחה מציין ששני מטענים חיוביים דוחים זה את זה.

נוסחה כללית לשדה אלקטרוסטטי

הפיתוח של נוסחת השדה החשמלי שיוצר מטען נקודתי, משמש בסיס למקרים כלליים ומורכבים יותר. בגלל עקרון הסופרפוזיציה, כאשר יש במרחב מספר מטענים נקודתיים סטטיים (שאינם נעים), מחשבים את השדה החשמלי שמפיק כל אחד מהם, והשדה הכללי המתקבל הוא סכום וקטורי של השדות של כל המטענים הנקודתיים. אם כל מטען $\ q_{i}$ נמצא בנקודה ${\vec {r}}_{i}$, הנוסחה לשדה החשמלי הכולל שיתקבל בכל נקודה $\ {\vec {r}}$ היא לפיכך $\ {\vec {E}}({\vec {r}})={k}\sum _{i}{{\frac {q_{i}}{|{\vec {r}}-{\vec {r}}_{i}|^{3}}}({\vec {r}}-{\vec {r}}_{i})}$.

בגבול שבו המטען החשמלי אינו אוסף של מטענים בדידים אלא הוא התפלגות מטען רציפה, כלומר כשאנחנו רוצים לחשב שדה שיוצר גוף טעון בעל נפח, הסכום הופך לאינטגרל:

${\vec {E}}({\vec {r}})={1 \over 4\pi \varepsilon _{0}}\iiint \limits _{V}\,{\rho ({\vec {r}}_{i}) \over ({\vec {r}}_{i}-{\vec {r}})^{2}}{\hat {\boldsymbol {r_{i}}}}dV$.

שלושת סימני האינטגרל מסמנים אינטגרציה בשלושת הממדים. האינטגרל סוכם את המטענים האינפיניטסימליים לאורך כל הנפח בו הם מפוזרים. כאשר $\ \rho ({\vec {R}})$מייצגת את פונקציית הצפיפות, פונקציה אשר מתאימה לכל נקודה במרחב את צפיפות המטען ביחס ליחידת נפח המצויה בו. במקרים שבהם פיזור המטען במרחב כפוף לסימטריה כלשהי (כגון תיל ארוך טעון או קליפה כדורית טעונה), ניתן לבחור מערכת קואורדינטות שמתאימה לסימטריה, ולהיעזר בה לחישוב השדה החשמלי שנובע ממטען זה. כך למשל, אם נתונה התפלגות מטען בעלת סימטריה כדורית, כדאי לנתח את הבעיה כשהיא מנותחת בקואורדינטות כדוריות, כי אז, משיקולי סימטריה, הרכיבים הזוויתיים של השדה החשמלי חייבים להיות אפס, ורק הרכיב הרדיאלי אינו מתאפס.

שטף חשמלי וחוק גאוס

ערך מורחב – חוק גאוס

בהינתן שדה חשמלי, נרצה מדד כלשהו להגדיר את מידת העוצמה שבה הוא פועל על משטח מסוים. מדד זה מוגדר מתמטית בעזרת שטף, על פי הנוסחה: $\Phi ={\vec {E}}\cdot {\vec {A}}=|{\vec {E}}||{\vec {A}}|\cos \theta$, כאשר ${\vec {A}}$ הוא הווקטור המוגדר על ידי המשטח, גודלו כשטח המשטח וכיוונו ניצב אליו. על פי ההגדרה, השטף תלוי בשלושה פרמטרים: בעוצמת השדה, בגודל המשטח, ובזווית שבה המשטח מוטה.

על פי חוק גאוס, אם נקח מעטפת העוטפת כמות מטענים, ישנו קשר ישיר וליניארי בין השטף של השדה החשמלי שהם יוצרים, לבין כמות המטענים שבתוך המעטפת, ללא תלות בצורת המעטפת ובשאר הנתונים של הבעיה. הקשר נקבע על פי הנוסחה: $\Phi ={\frac {Q}{\varepsilon _{0}}}$, כאשר ${\textstyle \Phi }$ הוא השטף החשמלי, $\ Q$ הוא המטען הכלוא בתוך המעטפת, ו-$\varepsilon _{0}$ הוא קבוע דיאלקטריות הריק.

החוק הוא יישום פיזיקלי של משפט גאוס המתמטי, והוא נכון במקרים רחבים יותר מהקשרו החשמלי. עם זאת, בחשמל חוק גאוס בצורתו הדיפרנציאלית נחשב לאחת מתוך ארבע משוואות מקסוול שפורסות באופן שלם את האלקטרומגנטיות, מה שמעיד על חשיבותו הרבה, ועל המשמעויות הרבות שנובעות ממנו. דוגמאות לשימוש בחוק יבואו בהמשך הערך.

הניסוח המתמטי המלא של החוק בצורתו האינטגרלית הוא: $\Phi =\int \!\!\!\!\!\!\!\subset \!\!\!\supset \!\!\!\!\!\!\!\int _{S}{\vec {E}}\,\cdot {\vec {\mathrm {d} A}}={\frac {1}{\varepsilon _{0}}}\int \!\!\!\!\!\int \!\!\!\!\!\int _{V}\rho \,\mathrm {d} V={\frac {Q}{\varepsilon _{0}}}$

כאשר ${\textstyle {\vec {E}}}$ הוא השדה החשמלי, ${\textstyle \mathrm {d} {\vec {A}}}$ הוא אלמנט שטח אינפיניטסימלי על המעטפת $\ S$, אשר כיוונו מוגדר כניצב למשטח, כלפי חוץ, $\rho \,$ הוא צפיפות המטען החשמלי בנקודה $V$, ו- ${\textstyle \oiint _{S}}$ הוא אינטגרל על המשטח הגיאוסי ${\textstyle \ S}$ המהווה מעטפת סביב נפח $\ V$.

גזירה מתוך הפוטנציאל החשמלי והמגנטי

השדה החשמלי מושרה כתוצאה מנוכחות מטען חשמלי (התפלגות מטען) או כתוצאה משינויים בזמן בשדה המגנטי. ליתר דיוק, השדה החשמלי מושרה על ידי הפוטנציאל החשמלי (זהו 4-וקטור) לפי הנוסחה:

$\ {\vec {E}}=-{\vec {\nabla }}\Phi -{\frac {1}{c}}{\frac {\partial }{\partial t}}{\vec {A}}$

כאשר $\Phi$ הוא הפוטנציאל הסקלרי ו-${\vec {A}}$ הוא הפוטנציאל הווקטורי.

שדות חשמליים של מטענים לא נקודתיים

שדה של כדור טעון

חוק גאוס מיושם לחישוב שדה שיוצר כדור טעון

בהינתן כדור שסך המטען עליו הוא $\ Q$, ופיזור המטען עליו אחיד.

שיקולי סימטריה מראים כי קווי השדה החשמלי שייווצרו מחוץ לכדור חייבים להיות מכוונים רדיאלית, כך שהם יהיו מאונכים לפני הכדור. את השדה שייווצר ניתן לחשב לפי חוק גאוס, תוך בחירת מעטפת כדורית שמרחקה ממרכז הכדור הוא $\ r$.

תחילה נחשב את השדה מחוץ לכדור. לפי החוק, עבור כל $\ r$ גדול מרדיוס הכדור עצמו (כלומר, כל נקודה מחוץ לכדור): $\epsilon _{0}\oint {\vec {E}}\cdot d{\vec {S}}=\Sigma q$. מאחר ששטחה של קליפה כדורית הוא $\ 4\pi r^{2}$ והשדה עליה קבוע מהסימטריה, מקבלים $\ \epsilon _{0}E4\pi r^{2}=Q$ או $\ E={\frac {1}{4\pi \epsilon _{0}}}{\frac {Q}{r^{2}}}={\frac {kQ}{r^{2}}}$ כאשר השיוויון האחרון נובע מערכיהם של הקבועים. כלומר, השדה החשמלי שיוצר כדור שטעון בצפיפות מטען אחידה, במרחב שמחוץ לו, הוא זהה לשדה שהיה יוצר מטען זהה שהוא נקודתי.

על מנת לחשב את השדה בתוכו תחילה יש לחשב את צפיפות המטען ליחידת נפח. מכיוון שהצפיפות אחידה: $\rho {\overset {\underset {\mathrm {def} }{}}{=}}{\frac {Q}{V}}={\frac {Q}{{\frac {4}{3}}\pi R^{3}}}$, כעת על מנת לחשב את השדה בנקודה מסוימת ברדיוס r בתוך הכדור נבנה מעטפת גאוס כדורית כך שמרכז המעטפת נמצא במרכז הכדור והנקודה מוכלת בשפתו. נשתמש בחוק גאוס: $\Phi =\int \!\!\!\!\!\!\!\subset \!\!\!\supset \!\!\!\!\!\!\!\int _{S}{\overrightarrow {E}}\,{\overrightarrow {\mathrm {d} S}}={\frac {1}{\varepsilon _{0}}}\int \!\!\!\!\!\int \!\!\!\!\!\int _{V}\rho \,\mathrm {d} V$. מכאן: $E\int \!\!\!\!\!\!\!\subset \!\!\!\supset \!\!\!\!\!\!\!\int _{S}ds=E\cdot 4\pi r^{2}={\frac {1}{\varepsilon _{0}}}\rho \,\int \!\!\!\!\!\int \!\!\!\!\!\int _{V}\mathrm {d} V={\frac {1}{\varepsilon _{0}}}\rho {\frac {4}{3}}\pi r^{3}$

נציב את הצפיפות הנפחית:

$E\cdot 4\pi r^{2}={\frac {1}{\varepsilon _{0}}}{\frac {4}{3}}\pi r^{3}\cdot {\frac {Q}{{\frac {4}{3}}\pi R^{3}}}={\frac {1}{\varepsilon _{0}}}Q\cdot {\frac {r^{3}}{R^{3}}}$

נבודד את השדה, את הכיוון אנחנו יודעים מפאת סימטריה כדורית שהוא רדיאלי.

${\vec {E}}=Q{\frac {r}{4\pi R^{3}\varepsilon _{0}}}{\hat {r}}$

בכדור מוליך

כאשר דנים בבעיות בהם החומר הוא מוליך, ידוע שהשדה בתוך התווך המוליך הוא שווה לאפס כל עוד אין המוליך מכיל מטענים מקובעים בתוכו (מה שאומר שהוא לא מוליך לגמרי אלא בין מוליך למבודד). עובדה זו נובעת מכך שכל המטענים מתרכזים על שפת המוליך, כתלות בנסיבות:

• בהיעדר שדה חיצוני, המטענים נדחים אחד מפני השני והולכים לקצוות.
• כאשר מופעל שדה חיצוני, האלקטרונים בתוך המוליך חופשיים לנוע בתגובה לשדה החיצוני, עד למצב שיווי משקל כך שהשדה הנוצר בין שפות המוליך מנוגד בכיוון לשדה המקורי ושווה לו בגודלו.

כיוון שכמות האלקטרונים גדולה בכמה סדרי גודל מכל שדה סטנדרטי שנוצר, יכולים האלקטרונים לבטל כל שדה סטנדרטי. לכן בתוך הכדור, אם ידוע שהוא מוליך, השדה הוא אפס.

שדה של תיל ארוך

בהינתן תיל שאורכו אינסופי, ושצפיפות המטען ליחידת אורך עליו היא $\lambda$, שיקולי סימטריה מראים כי קווי השדה החשמלי שייווצרו מחוץ לתיל חייבים להיות מאונכים לתיל. משיקולים דומים יהיה השדה החשמלי שהתיל מפעיל תלוי רק במרחק מהתיל. בגלל הסימטריה הגלילית מחשבים את השדה לפי חוק גאוס תוך שימוש במעטפת בצורת גליל, שמוצבת מסביב לתיל. מכיוון שהשדה מאונך לתיל (ולמעטפת הגליל), השטף שלו יהיה מקסימלי דרך מעטפת הגליל, ו-0 דרך בסיסי הגליל. השדה במרחק $\ r$ מהתיל יהיה:

$\epsilon _{0}\oint {\vec {E}}\cdot d{\vec {S}}=\Sigma q$

$\ \epsilon _{0}E2\pi rl=\lambda l$

$\ l$ מציין יחידת אורך מסוימת – את אורך המוט המוגבל על ידי המעטפת הגלילית. אין זה משנה איזה אורך בוחרים, מאחר שהוא מצטמצם בחישוב:

$\ E={\frac {\lambda }{2\pi r\epsilon _{0}}}$

תוצאה זו נכונה כל עוד המרחק מהמוט זניח ביחס לאורך המוט, שכן המודל מניח כאמור מוט שאורכו אינסופי.

שדה של לוח אינסופי

אם על פניו של לוח אינסופי מפוזר באופן אחיד מטען כלשהו, כך שצפיפותו ליחידת שטח היא $\ \sigma$, ניתן לראות, כתוצאה משיקולי סימטריה, שהשדה החשמלי שהוא מפעיל יהיה מאונך לפני הלוח. כמו כן אין זה משנה מול איזה חלק של הלוח יוצב המטען המושפע מהשדה (בהנחה שהלוח אינסופי או שהמרחקים קטנים מאוד), כי גודל עוצמת השדה יושפע רק ממרחק המטען מהלוח. המעטפת הגלילית שנבחר לצורך השימוש בחוק גאוס תהיה מאונכת ללוח, ואחד מבסיסי הגליל שלנו יעבור בדיוק באמצעו. אם מדובר בלוח מוליך, לא יהיה בתוכו שדה חשמלי. קווי השדה היוצאים מהלוח יהיו מאונכים לבסיס השני של הגליל ומקבילים למעטפת שלו, כך שרק דרך הבסיס האחד יעבור שטף חשמלי. עתה נחשב את השדה במרחק r מהלוח המוליך:

$\ \epsilon _{0}\oint {\vec {E}}\cdot d{\vec {S}}=\sum {q}$
$\ 2\epsilon _{0}EA=\sigma A$
$\ E={\frac {\sigma }{2\epsilon _{0}}}$

בדומה למקרה הקודם, גם כאן A מציינת יחידת שטח זמנית – את שטח בסיס הגליל שדרכו עובר השטף, ואת השטח על פני הלוח שתופסים המטענים הכלואים במעטפת הגלילית. התוצאה הזאת מפתיעה שכן קיבלנו חוסר תלות גם במרחק מהלוח, מה שאומר תיאורתית שאם הלוח אינסופי אז השדה בכל נקודה במרחב כולו יהיה שווה, והשדה תלוי אך ורק בצפיפות המטען של הלוח. מובן שכל האמור נכון רק ללוח אינסופי או למרחק קטן מאוד מלוח טעון גדול מאוד.

השדה במקרה של קבל לוחות הוא סופרפוזיציה של השדות של שני הלוחות והוא: $E={\frac {\sigma }{\epsilon _{0}}}$ בין הלוחות, ואפס מחוץ לקבל.

ראו גם

• שדה אלקטרומגנטי
• טנזור השדה האלקטרומגנטי
• משוואות מקסוול

קישורים חיצוניים

• שדה חשמלי, באתר אנציקלופדיה בריטניקה (באנגלית)
• שדות חשמליים, דף שער בספרייה הלאומית

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

שדה חשמלי37654310Q46221