שארית של טור טיילור

גרף של $f(x)=e^{x}$ יחד עם הקירוב הלינארי שלו $P_{1}(x)=1+x$ סביב a = 0.

גרף של $f(x)=e^{x}$ (בכחול) יחד עם הקירוב הריבועי שלו $P_{2}(x)=1+x+x^{2}/2$ (באדום) סביב a = 0. שים לב לשיפור בקירוב.

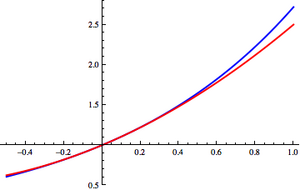
באנליזה מתמטית, השארית של טור טיילור מסדר n של פונקציה, היא ההפרש בין ערך הפונקציה לבין ערכו של סכום n הרכיבים הראשונים בטור טיילור שלה. מכיוון שהטור (האינסופי) אמור להתכנס אל הפונקציה בנקודה, השארית מתארת השגיאה שבהחלפת הפונקציה בסכום חלקי של הטור. הכללה של משפט ערך הביניים מאפשרת לחסום את השגיאה, בתנאי שאפשר לחסום את הנגזרת ה-n+1 של הפונקציה בקטע $(x_{0},a)$, כאשר a היא הנקודה סביבה מפתחים את הטור ו-$x_{0}$ היא הנקודה בה מחושב ערך הפונקציה.

אינטואיציה

אם פונקציה ממשית f היא גזירה בנקודה a אז יש לה קירוב לינארי בנקודה a. זה אומר שקיימת פונקציה h₁ כך ש-:

$f(x)=f(a)+f'(a)(x-a)+h_{1}(x)(x-a),\qquad \lim _{x\to a}h_{1}(x)=0.$.

כאן $P_{1}(x)=f(a)+f'(a)(x-a)\$

הוא הקירוב הלינארי של f בנקודה a. הגרף של $P_{1}(x)=f(a)+f'(a)(x-a)\$ הוא הקו המשיק לגרף של f ב-$x=a$. השגיאה בקירוב היא: $R_{1}(x)=f(x)-P_{1}(x)=h_{1}(x)(x-a)\$.

אם היינו רוצים קירוב טוב יותר ל-f, היינו מתחשבים גם בשינוי השיפוע של f, כלומר בנגזרת השנייה של f ב-$x=a$ - כלומר נקרב את הפונקציה קירוב ריבועי על ידי פולינום ריבועי במקום פונקציה לינארית. במקום להשתמש בנגזרת אחת של f ב-a, ניתן להשתמש בשתי נגזרות, וכך להשתמש בפולינום שיש לו אותו שיפוע וקעירות כמו לפונקציה f בנקודה a. הפולינום הריבועי שמתקבל הוא:

$P_{2}(x)=f(a)+f'(a)(x-a)+{\frac {f''(a)}{2}}(x-a)^{2}.\,$.

באופן דומה, ניתן לקרב את הפונקציה על ידי פולינום מסדר שלישי ורביעי וכן הלאה. משפט השארית קובע שהשגיאה תמיד תלויה בקצב השינוי של הנגזרת ה-n (כלומר בנגזרת ה-n+1) בנקודת ביניים בקטע שבו נעשה נעשה הפיתוח. אינטואיציה לנכונות הטענה היא שכל הנגזרות מסדר n + 2 ומעלה כבר "מובלעות" בהתנהגות של הנגזרת ה-n+1 בקטע בו נעשה הפיתוח, ולכן הערך הממוצע של $f^{(n+1)}$ בקטע (a,x₀) כבר מכיל את המידע על ההתנהגות של נגזרות מסדרים גבוהים יותר.

המשפט וההוכחה

משפט השארית קובע שהשארית שווה ל-: $R_{k}(x)={\frac {f^{(k+1)}(\xi _{L})}{(k+1)!}}(x-a)^{k+1}$, כאשר $\xi _{L}$ היא הנקודה בה מתקבל ערך הביניים של $f^{(n+1)}$ בקטע (x,a).

הוכחה:

נכתוב את השארית של קירוב טיילור מסדר n הנעשה סביב x = a, השארית היא: $R_{n}(x)=f(x)-f(a)-{\frac {f'(a)}{1!}}(x-a)-...-{\frac {f^{(n)}(a)}{n!}}(x-a)^{n}$. השארית היא פונקציה רציפה ומקבלת בקצוות הקטע (a,x) את הערכים: $R_{n}(a)=0,R_{n}(x)=R_{n}(x)$. נוסף לזה, בקטע (a,x) פונקציית השארית גזירה ולכן, אם נתייחס ל-a כאל משתנה, נקבל:

$R_{n}'(x)=-f'(a)-(f''(a)(x-a)-f'(a))-({\frac {f'''}{2!}}(x-a)^{2}-f''(a)(x-a))-...-({\frac {f^{(n+1)}(a)}{n!}}(x-a)^{n}-{\frac {f^{(n)}(a)}{(n-1)!}}(x-a)^{(n-1)})$. תוצאה זו מתקבלת על ידי גזירת כל אחד מהאיברים בביטוי לשארית לפי כלל המכפלה של לייבניץ. זהו טור טלסקופי ולכן לאחר צמצום איברים מתקבל רק האבר האחרון:

(1) $R_{n}'(a)=-{\frac {f^{(n+1)}(a)}{n!}}(x-a)^{n}$.

תהי עתה $\phi (a)$ פונקציה מוגדרת ורציפה בקטע הסגור [a,x]. לפי משפט הערך הממוצע של קושי קיימת נקודה $a<\xi _{L}<x$ כך ש-:

${\frac {R_{n}(x)-R_{n}(a)}{\phi (x)-\phi (a)}}={\frac {R_{n}'(\xi _{L})}{\phi '(\xi _{L})}}$.

אם נציב $a=\xi _{L}$ בתוצאה (1) נקבל:

(2) $R_{n}(x)={\frac {\phi (x)-\phi (a)}{\phi '(\xi _{L})}}*{\frac {f^{(n+1)}(\xi _{L})}{n!}}(x-\xi _{L})^{n}$.

נבחר $\phi (a)=(x-a)^{(n+1)}$. כיוון ש-$(x-a)^{(n+1)}$ מקיים את כל התכונות הדרושות כדי להבטיח את תקפות משפט קושי, ולכן מתקבלת הנוסחה הבאה עבור השארית: $R_{n}(x)={\frac {\phi (x)-0}{\phi '(\xi _{L})}}*{\frac {f^{(n+1)}(\xi _{L})}{n!}}(x-\xi _{L})^{n}={\frac {(x-a)^{(n+1)}}{(n+1)(x-a)^{n}}}*{\frac {f^{(n+1)}(\xi _{L})}{n!}}(x-\xi _{L})^{n}={\frac {f^{(n+1)}(\xi _{L})}{(n+1)!}}(x-\xi _{L})^{n}*(x-a)={\frac {f^{(n+1)}(\xi _{L})}{(n+1)!}}(x-\xi _{L})^{(n+1)}$

הביטוי לשארית נקרא השארית בצורת לגראנז'.

דוגמאות

• נניח כי ברצוננו להעריך את הקבוע המתמטי e. מתקיים: $(e^{x})^{(n)}=e^{x}$. כמו כן פיתוח טיילור מסדר n של פונקציית האקספוננט סביב a = 0 הוא $e^{x}\approx 1+x+...+{\frac {x^{n}}{n!}}$. לכן מתקיים: $R={\frac {f^{(n+1)}(x)}{(n+1)!}}*(1-0)^{n+1}$ כאשר x בקטע $(0,1)$. ערכה המרבי של הנגזרת $f^{(n+1)}(x)$ בקטע (0,1) מתקבל בקצה הקטע, כלומר ב-x = 1 לכן מתקיים:

$R<{\frac {f^{(n+1)}(1)}{(n+1)!}}={\frac {e^{1}}{(n+1)!}}={\frac {e}{(n+1)!}}$ . כיוון שידוע ש-$e<3$ מתקבלת התוצאה: $R<{\frac {3}{(n+1)!}}$.

• נניח כי ברצוננו להעריך את $\pi /4=arctan(1)$ בהתאם לנוסחת לייבניץ לפאי. מתקיים : $arctan(x)=x-x^{3}/3+x^{5}/5-...$ (כאשר $|x|$ לכל היותר 1). מן הצורה המתמטית של פיתוח טיילור של $arctan(x)$ נובע ש-$f^{(2n+1)}(0)=(-1)^{(n+1)}(2n)!$, לכן נקבל שהשארית בחישוב $arctan(1)$ היא $R<{\frac {1}{2n+1}}$, כלומר הטור מתכנס לאט מאד (עקב העלייה המהירה בנגזרות של $arctan(x)$).