עידוש כבידתי

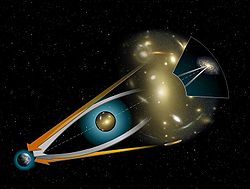
עידוש כבידתי - איור

עידוש כבידתי (באנגלית: Gravitational Lensing) הוא תופעה בה קרני אור מתעקמות סביב גוף בעל מסה ועקב כך יוצרות תופעות אופטיות של הסחה, הגברה ועיוות בדמות של העצם. התופעה של עידוש כבידתי היא חיזוי של תורת היחסות הכללית שפיתח אלברט איינשטיין והייתה אחד המבחנים הראשונים לאישושה. כיום, תופעה זו מוצאת שימוש רב באסטרונומיה ככלי לבצע תצפיות ולחקור את היקום.

תיאור התופעה

מבוא

צילום של עידוש כבידתי כפי שצולם על ידי טלסקופ החלל ג'יימס ווב. הגדילו את התמונה כדי לצפות בדמויות המעודשות.

תקריב של אזור מהתמונה הקודמת ובו דמויות של עידוש כבידתי מוקפות בעיגול.

עידוש כבידתי היא תופעה בה גרביטציה מעצם מאסיבי (עצם עם הרבה מסה) מעקמת את קרני האור, בצורה דומה לעדשה. כתוצאה מכך, המסלול של האור מהמקור מתעקם, ומתקבלת דמות מעוותת. יתרה מכך, מיקומה של הדמות בשמים שונה ממיקומו של המקור ולעיתים קרובות רואים מספר דמויות של אותו האובייקט ולא דמות אחת. כאשר המקור, העדשה והצופה נמצאים על ציר אחד, הדמות של המקור מתעוותת לטבעת המקיפה את העדשה (הנקראת טבעת איינשטיין, Einstein ring). תופעה זו הוזכרה לראשונה על ידי אורסט חבולסון (Orest Khvolson) ב-1924 ונוסחה באופן מתמטי על ידי אלברט איינשטיין ב-1936. בדרך כלל, המקרים בהם העצם נמצא בדיוק על ציר העדשה הם נדירים, ולכן ניתן לראות מספר דמויות מעוותות לצורת קשת. באמצעות ניתוח הדמויות בשמים ניתן ללמוד על התפלגות המסה בעדשה (למשל: מהי מסת העדשה) ולהפך: כאשר ידועה מהי התפלגות המסה באזור העדשה, ניתן לחשב מהן הדמויות שיראו בשמים.

הסבר לתופעה

לפי תורת היחסות הכללית, נוכחות של מסה-אנרגיה-לחץ במרחב-זמן מעקמת את המרחב-זמן ואת ההתעקמות של המרחב-זמן אנו מזהים כשדה גרביטציה. מאחר שגוף מסיבי (בעל מסה רבה) מעקם את המרחב שסביבו, כל העצמים שנעים בסביבתו נעים במסלולים עקומים, שהם גיאודזות במרחב עקום. לפי תורת היחסות הכללית, גם האור לא יכול להתעלם מהעקמומיות של המרחב (וזאת בניגוד לכבידה הניוטונית), ולכן גם קרני אור ופוטונים ("חלקיקי" אור) ינועו בקווים עקומים. כתוצאה מכך, קרני האור – הנעים בקו ישר – יתעקמו ליד גוף מסיבי, במידה התלויה במסת הגוף ובמרחקם ממנו.

בפיזיקה, ובייחוד באופטיקה, קוראים לכל תופעה בה קרני האור משנות את מסלולן (למשל, כגון בשבירה) בשם "עידוש". לכן, לתופעה שבה קרני האור משנות את מסלולן בגלל השפעות כבידה קוראים "עידוש כבידתי". שימוש מצומצם יותר במונח מתייחס לתופעה הפרטית שבה גוף מסיבי בעל סימטריה כדורית (להבא גוף כזה יקרא "ספרי" מהמילה sphere) מקורבת פועל באופן אנלוגי לעדשה אופטית רגילה המוכרת לנו מחיי היום יום.

גוף מסיבי ספרי פועל כמו עדשה קמורה וממקד את קרני האור העוברים לידו בנקודה מסוימת, בה הוא יוצר דמות. כאשר העצם, העדשה והדמות (או ליתר דיוק: הצופה הרואה את הדמות) נמצאים על ציר אחד, בגלל הסימטריה הגלילית של הבעיה הדמות שמתקבלת מתעוותת לצורה טבעת המקיפה את העדשה (הגוף המסיבי ספרי שמבצע את העידוש הכבידתי). טבעות אלה נקראות "טבעות איינשטיין" ואפשר לחשב את הזווית שהן יוצרת בשמים. כאשר העצם לא נמצא בדיוק מאחורי העדשה (כלומר: בדיוק על ציר העדשה) הסימטריה הגלילית נשברת ומתקבלות רק שתי דמויות (דמות אחת מקרן שמתעקמת מ"למעלה" ודמות שנייה מקרן שמתעקמת מ"למטה"), שכל אחת מתעוות למעין קשת (על טבעת איינשטיין) בהתאם למידה של כמה העצם סוטה מלהיות ממש מאחורי העדשה (ככל שהעצם נמצא בדיוק מאחורי העדשה, כך הקשת שאליה הדמות נמרחת היא גדולה יותר וקרובה להשלים את כל הטבעת).

סוגים של עידוש כבידתי

ישנים 3 מחלקות, או סוגים, של עידוש:

1. עידוש חזק (Strong lensing): כאשר את העידוש ניתן לראות באופן אופטי, כלומר: ניתן לצפות בטלסקופ בדמויות מעוותות או טבעות איינשטיין.
2. עידוש חלש (Weak lensing): כאשר ההפרעות שיוצר העידוש חלשות מאוד וניתן לגלותן רק באמצעות ניתח של העיוותים של עצמים ברקע.
3. מיקרו-עידוש (Microlensing): כאשר לא ניתן לראות שום עיוות אופטי בעצמי הרקע, אלא רק שינוי בבהירות (עוצמת ההארה) שלו. בדרך כלל, באירועי מיקרו-עידוש, הבהירות משתנה עם הזמן כאשר "הר" בעקומת הבהירות מרמז שעבר בין העצם לצופה גוף מסיבי שביצע עידוש כבידתי לעצם. תופעה זו יכולה לשמש לאיתור כוכבי לכת חיצוניים.

עדשות כבידה משפיעות על כל סוגי הקרינה האלקטרומגנטית, ולא רק על האור הנראה. אסטרונומים חוקרים עידוש חלש באמצעות קרינת הרקע הקוסמית ואילו עידוש חזק נצפות ונחקרות גם באמצעות אור נראה, גלי רדיו וקרינת רנטגן.

עקרונות מתמטיים

במקרה שבו המרחק בין קרן האור לגוף המסיבי גדול מאוד מרדיוס שוורצשילד, שדה הכבידה הפועל על הקרן חלש יחסית. קירוב זה נקרא "קירוב השדה החלש" (או באופן אנלוגי לאופטיקה: "קירוב העדשה הדקה"). בקירוב זה אפשר לעבוד עם קירוב זוויות קטנות ( $\ \theta \approx \sin \theta \approx \tan \theta$ ) ניתן לחשב את זווית ההסחה שיוצרת עדשה כבידתית בעלת סימטריה כדורית ומסה M. זווית זו נתונה על ידי

איור המציג עידוש כבידתי כאשר העצם, העדשה והצופה נמצאים על אותו ציר

$\ \alpha ={\frac {4GM}{c^{2}b}}={\frac {2r_{s}}{b}}$

כאשר:

• G הוא קבוע הכבידה של ניוטון
• c היא מהירות האור
• M היא מסת ה"עדשה"
• b הוא המרחק של קרן העוברת לבין מרכז העדשה
• r_s הוא רדיוס שוורצשילד של ה"עדשה"

הזווית $\ \theta _{E}$ בין הדמות הנצפית לציר העדשה נקראת "זווית איינשטיין". אם אנו יודעים את המרחק לעצם, אזי אפשר לחשב את הרדיוס של טבעת איינשטיין על ידי $\ r_{E}\approx D_{OS}\theta _{E}$. את זווית איינשטיין אפשר לחשב באמצעות הנוסחה לעיל והגאומטריה של הבעיה, אם מבצעים את החישוב מקבלים ש

$\ \theta _{E}={\sqrt {{\frac {4GM}{c^{2}}}{\frac {D_{LS}}{D_{OL}D_{OS}}}}}$

זווית איינשטיין היא אחת הפרמטרים החשובים בעידוש כבידתי. היא קובעת את מידת ההפרדה של הדמויות מהעדשה ואחת מהשנייה וכן את עוצמת ההגדלה (כאשר העצם לא על ציר העדשה).

במקרה שהמקור (S) נמצא בזווית $\beta$ מעל ציר העדשה נשברת הסימטריה הגלילית ויש לנו מישור מובחן: המישור שכולל את הצופה, הדמות, העדשה וציר העדשה. במקרה זה יתקבלו שתי דמויות, שזוויות איינשטיין שלהן הן

$\ \theta _{+}={\frac {\beta +{\sqrt {\beta ^{2}+4\theta _{E}^{2}}}}{2}}\ \quad ;\quad \theta _{-}={\frac {\beta -{\sqrt {\beta ^{2}+4\theta _{E}^{2}}}}{2}}$

עוצמת ההגברה נתונה על ידי היחס בין סכום השטחים הזוויתיים של הדמויות לשטח הזוויתי של המקור. ניתן לחשב ולהראות שההגברה A על ידי

$\ A={\frac {(\beta /\theta _{E})^{2}+2}{(\beta /\theta _{E}){\sqrt {(\beta /\theta _{E})^{2}+4}}}}$

עבור מקורות שנמצאים כמעט על ציר העדשה (כלומר: $\ \beta <<\theta _{E}$) מתקיים שההגדלה הולכת כ $\ A\sim \theta _{E}/\beta$ . יש אומנם התבדרות כאשר $\ \beta =0$ אך מקרה זה קורה רק כאשר מקור נקודתי נמצא בדיוק על הציר העדשה ואז יוצר טבעת איינשטיין, ולכן ההגדלה של נקודה למעגל היא פי אינסוף. בפועל, מאחר שאין מקורות נקודתיים, ההתבדרות לעולם אינה מתרחשת.

שימושים באסטרונומיה

טבעת איינשטיין

• עדשה כבידתית לצפייה בעצמים (גלקסיות, קווזרים, כוכבים וכו) המוסתרים מאחורי עצם אחר
• שימוש בהגברה שיוצרת עדשה כבידתית על מנת לראות עצמים רחוקים במיוחד
• ניסויים לבדיקת קיומו של חומר אפל המפוזר בגושי MACHO
• גילוי כוכבי לכת חוץ-שמשיים
• גילוי קיומם של חורים שחורים

הגברת בהירות כבידתית

כאשר דמות של עצם מתעוותת לצורה של קשת (שהיא חלק מטבעת איינשטיין) הגודל שלה על השמיים גדל, וכתוצאה מכך גם הבהירות נראית (Luminosity) שלו גדלה (בהירות היא עוצמת ההארה של הגוף, כלומר: שטף הקרינה שלו ליח' זמן או הספק הקרינה הנצפה). כאשר הבהירות של עצם גדלה, קל יותר לראות אותו באמצעות מכשור אופטי (כגון טלסקופ). מאחר שהבהירות הנצפית של עצם יורדת ככל שהוא נמצא יותר רחוק מאיתנו, השימוש בהגברה כבידתית מאפשר לראות עצמים שבאופן רגיל לא היינו רואים כי הם חיוורים מידי עבור ציוד התצפית שברשותינו.

בדיקת קיומו של חומר אפל

אחת התאוריות בנוגע למהותו של החומר האפל טוענת שסביב כל גלקסיה מרחפים גופים דחוסים וקומפקטים המכילים מסה רבה אך חוורים מאוד ולא מבצעים כמעט אינטראקציה הפולטת קרינה. גופים אלה נקראים MACHO, ראשי תיבות של Massive Compact Halo's Objects (כלומר: גופים מסיביים וקומפקטים של הילת הגלקסיה).

באמצעות עידוש כבידתי אפשר לבדוק את התאוריה הזו. אסטרופיזיקאי פולני בשם פצינסקי (Paczynzki) הציע ב-1986 ניסוי לבדיקת תאוריית ה־MACHO המתבסס על תצפיות של עידוש כבידתי בכוכבים של הענן המגלני הגדול.

מהערכה של מסת החומר האפל סביב הגלקסיה שלנו וההערכה למסה של כל MACHO (מהערכה זו אפשר לחשב את צפיפות ה־MACHO-ים סביב הגלקסיה). כל MACHO כזה יכול לבצע עידוש כבידתי כאשר הוא חולף ביננו לבין כוכב אחר. בעידוש זה ניתן להבחין בתצפית, על ידי זיהוי הגברה פתאומית בבהירות כוכב כלשהו ואז דעיכה מהירה וסימטרית (נוצרת מעין עקומת פעמון של הבהירות כתלות בזמן, שמייצגת גוף מסיבי עדש שחלף ביננו לבין העצם, ברגע השיא - העדשה נמצאת על קו הראייה ביננו לעצם).

כעת נסתכל בענן המגלני הגדול, גלקסיה קטנה הנמצאת יחסית קרוב אלינו (מרחק של 50 קילו-פרסק. במרחק זה ניתן להפריד אופטית את הכוכבים בענן). לפי התאוריה לגבי קיומם ופיזורם של MACHO אפשר להעריך את כמות העידושים שיתבצעו בפרק זמן נתון. החישוב מראה שהתוצאה של מספר האירועים לא תלויה במסה של כל MACHO אלא רק במסה הכוללת, ומקבלים ש

$\ {\mbox{Number of Lensing Amplification}}\ \equiv N\approx {\frac {GM_{dm}}{r_{MW\to LMC}c^{2}}}$

כאשר $\ r_{MW\to LMC}=50{\mbox{kPc}}$ הוא המרחק בין שביל החלב לענן המגלני הגדול, ואילו M_dm היא מסת החומר האפל שנמצאת בהילה של MACHO-ים סביב הגלקסיה. לפי מדידות עקומות סיבוב של הגלקסיה והערכות קינמטיות, החומר האפל שסביב הגלקסיה מכיל מסה מסדר גודל של 10¹² מסות שמש. בהצבת כל הנתונים וההערכות מקבלים שבכל רגע נתון אחד מתוך מיליון כוכבים בענן המגלני הגדול עובר עידוש כבידתי בגלל MACHO.

בהתבסס על נתונים אלה אפשר להעריך מהי תדירות העידושים שנראה, וכמה זמן יימשך עידוש ממוצע, בהתאם להרכבם של ה MACHO-ים (האם הם בגודל ובמסת השמש, או האם הם בגודל ומסה של כוכב כמו צדק?). לכן, יש לצפות בענן המגלני למשך תקופה ארוכה (לפחות 5 שנים) ולספור כמה עידושים רואים, ואז להשוות את זה לתחזיות התאורטיות השונות. ניסוי כזה התבצע ב-1991 וכמות אירועי העידוש שנמדדה בו הייתה נמוכה בהרבה מהכמויות אותן חוזות התאוריות התומכות ב־MACHO-ים. לפי התוצאות, העריכו האסטרופיזקאים שמספר הגופים דמויי ה־MACHO בהילת הגלקסיה מהווים לכל היותר רק 20% מהמסה האפילה שאותם מחפשים האסטרונומים. כלומר, ניסוי זה שלל את תאוריית ה־MACHO כפתרון מלא לבעיית החומר האפל.

לקריאה נוספת

• OGLE

קישורים חיצוניים

• עידוש כבידתי, הסבר קצר בליווי תרשימים באתר של נאס"א (באנגלית)
• על עדשות כבידה, מאת פיט ניוברי, באתר המכון למתמטיקה יישומית של אוניברסיטת קולומביה הבריטית (באנגלית)
• עידוש כבידתי, באתר אוניברסיטת הרווארד (באנגלית)
• אתר המסביר כיצד למדל עידוש כבידתי בתוכנה גרפית, מכיל שרטוטים ומשוואות בנוגע לתיאור הגאומטרי של התופעה (באנגלית)
• כיצד עידוש כבידתי משפיע על הדמות המתקבלת, סימולציה נחמדה באוניברסיטת הרווארד המדגימה כיצד עדשות כבידה מעוותות תמונות של טירות עתיקות. בנוסף כולל האתר תצלומים אמיתיים של עידוש כבידתי כפי שניצפה בחלל החיצון על ידי טלסקופים.(באנגלית)
• ארז גרטי, עידוש כבידתי – מבט אל עומק היקום, במדור "מאגר המדע" באתר של מכון דוידסון לחינוך מדעי, 7 ביולי 2011
• הערך עידוש כבידתי באתר אסטרופדיה
• אליה ליבוביץ, עדשת הכבידה, מדע, מרץ 1981
• עידוש כבידתי, באתר אנציקלופדיה בריטניקה (באנגלית)
• אשכול כתבות באתר של מכון דוידסון לחינוך מדעי
• אשכול כתבות באתר "הידען"
• עידוש כבידתי, סרטון בערוץ "Fermilab", באתר יוטיוב (אורך: 7:14), 24 ביוני 2015 (באנגלית)
• הגדלת האור פי 100 מיליארד עם עידוש כבידתי סולארי כדי לדמות כוכב לכת חוץ־שמשי, הרצאה בערוץ "KISSCaltech", באתר יוטיוב (אורך: 54:10), 18 במאי 2018 (באנגלית)

הערות שוליים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

עידוש כבידתי34290768Q185243