קירוב זווית קטנה

קירוב זוויות קטנות הוא קירוב מתמטי המפשט את חוקי הטריגונומטריה עבור זוויות קטנות, דהיינו זוויות בגבול לאפס.

הקירוב מבוסס על הגבול $\lim _{x\to 0}{\frac {\sin(x)}{x}}=1$, כאשר הזווית $x$ נמדדת ברדיאנים. כתוצאה מכך ניתן לקרב את הפונקציות הטריגונומטריות לפונקציות ליניאריות:

${\begin{aligned}\sin(x)\approx x\\\cos(x)\approx 1\\\tan(x)\approx x\end{aligned}}$

קירוב זוויות קטנות שימושי מאד בניתוח מערכות פיזיקליות, כולל בתחומי מכניקה, אופטיקה, אלקטרומגנטיות ואסטרונומיה. הקירוב מפשט משוואות דיפרנציאליות מסובכות למשוואות ליניאריות פתירות. למשל, מטוטלת מתמטית בקירוב זוויות קטנות היא מתנד הרמוני, שפתרונו מוכר.

שיקולים גאומטריים לקירוב

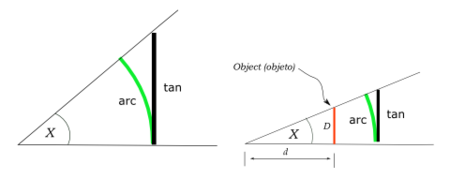
הפונקציות הטריגונומטריות מוגדרות כיחסים בין הצלעות של משולש ישר-זווית. הקשת הירוקה, בזווית $x$, שייכת למעגל ברדיוס יחידה. כתוצאה מכך אורך הקשת שווה ל־$x$.

ניתן לראות שכאשר הזווית $x$ קטנה, אורך הניצב הסמוך לזווית הופך דומה לאורך היתר. כלומר היתר שווה בערך לצלע הסמוכה לזווית, כך שהקוסינוס שווה בערך ל־1. כמו כן, אורך הצלע שמול הזווית הופך דומה לאורך הקשת, ולכן היחס בינה לבין הצלע הסמוכה או בינה לבין היתר, הלא הם ערכי הפונקציות סינוס וטנגנס, שווים בקירוב לגודל הזווית.

שיקולים אנליטיים לקירוב

הקירובים הללו זהים לקירוב טור מקלורן מסדר ראשון. טורי טיילור המתאימים לפונקציות הטריגונומטריות השונות הם כלהלן:

${\begin{aligned}\sin(x)=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots \\\cos(x)=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\cdots \\\tan(x)=x+{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}+{\frac {17x^{7}}{315}}+\cdots \end{aligned}}$

כאשר $x$ הזווית ברדיאנים. עבור ערכי $x$ קטנים, החזקות הגבוהות של $x$ דועכות במהירות לאפס, כך שניתן להזניח את האברים הללו ולהכליל אך ורק את החזקה הנמוכה ביותר, היא החזקה הליניארית עבור סינוס וטנגנס, והקבוע 1 עבור קוסינוס. כדי להגדיל את הדיוק של הקירוב ניתן להוסיף את האברים של החזקות הבאות. הקירוב מסדר שני של הסינוס והטנגנס שווה לקירוב מסדר ראשון, בקוסינוס לעומת זאת קיים אבר מסדר שני, ולכן הקירוב המדויק יותר מסדר שני כולל שני אברים:

$\cos(x)\approx 1-{\frac {x^{2}}{2}}$

ראו גם

• קירוב ליניארי
• הקירוב הפראקסיאלי

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0