מעבר פאזה קוונטי

מעבר פאזה קוונטי (באנגלית: QPT - Quantum Phase Transition) הוא מעבר פאזה בין מצבים קוונטים שונים של מערכת בטמפרטורת האפס המוחלט. בניגוד למעברי פאזה קלאסיים, מעברי פאזה קוונטיים יתרחשו על ידי שינוי פרמטר פיזיקלי - כגון לחץ או שדה מגנטי - בטמפרטורת האפס המוחלט. מעבר הפאזה מתאר שינוי פתאומי במצב היסוד של המערכת עקב תנודות קוונטיות הנובעות מעיקרון האי-ודאות של הייזנברג.

תאוריה בסיסית למעברי פאזה קוונטיים

איור 1: רמות אנרגיה במערכת דו גופית. ככל שממדי המערכת גדלים, כך רמות האנרגיה מתקרבות אחת לשנייה, עד לחצייתם. בנקודת החצייה, המערכת בגבול התרמודינמי ומצב היסוד שלה משתנה.

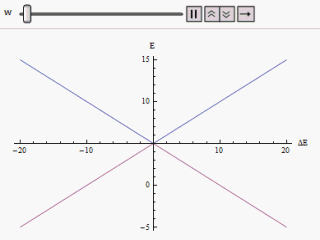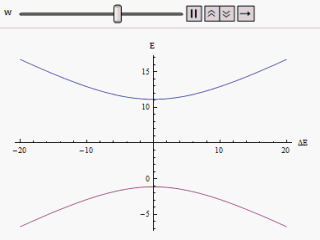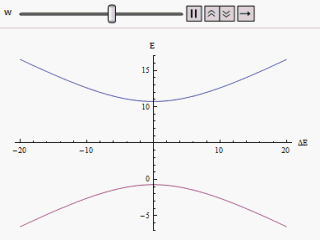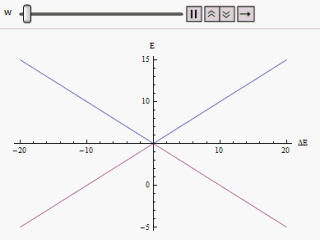
לגביש הנמצא בטמפרטורה $T=0$ עם אנרגיה המתוארת על ידי המילטוניאן מהצורה $H(g)=H_{0}+gH_{1}$, כאשר $g$ הוא פרמטר צימוד חסר ממדים, ומקיים את יחסי החילופיות $[H_{0},H_{1}]\neq 0$, רמות האנרגיה תלויות בממדי המערכת. גביש עם ממדים סופיים יציג רמות אנרגיה שאינן חוצות זו את זו (avoided level-crossing) וככל שנגדיל את ממדי המערכת רמות האנרגיה יתקרבו אחת לשנייה עד שלבסוף, בגבול התרמודינמי, יחצו זו את זו (level-crossing). בנקודת החציה האנרגיה $E(g)$ (שהיא שווה לאנרגיה החופשית כיוון שהטמפרטורה שווה לאפס) הופכת ללא-אנליטית ובכך מצביעה על מעבר פאזה. כזכור, טמפרטורת המערכת היא אפס ולכן מעבר פאזה זה אינו תרמי אלא קוונטי. כדי להבין זאת נסתכל על איברי ההמילטוניאן, $H_{0}$ ו- $H_{1}$, כעל איברים המתחרים ביניהם על מצבים קוונטים שונים של המערכת. כאשר $g<<1$, מצב היסוד של המערכת, שהוא המצב האנרגטי המינימלי של המערכת, נובע בעיקר מתרומה של $H_{0}$ עם תנודות המושפעות מ- $H_{1}$. וכאשר $g>>1$, מצב היסוד של המערכת הוא $H_{1}$ בעיקרו. בנקודת החציה, $g=g_{c}$, מתרחש מעבר פאזה המסמל את שינוי הדומיננטיות היחסית של $H_{0}$ ו- $H_{1}$. נקודת מעבר הפאזה נקראת נקודה קריטית קוונטית.

אנלוגיה בין מעברי פאזה קלאסיים וקוונטים

בטמפרטורה שאינה אפס, המצב המיקרוסקופי של המערכת, המאופיין במיקום ובתנע של כל חלקיק במערכת, אינו בשיווי משקל עקב תנודות תרמיות בחומר, אלא עובר בין מצבים באופן אקראי, בהסתברות הנתונה על ידי התפלגות בולצמן. מעברי פאזה הנובעים מתנודות תרמיות נקראים מעברי פאזה תרמיים (גם מעברי פאזה קלאסיים) והם תלויים בטמפרטורה בה המערכת נמצאת. קימות דוגמאות רבות למעברי פאזה קלאסיים בחיי היום יום, למשל הפיכת מים נוזליים לקרח מתחת לטמפרטורה של 0°C‏, ודוגמאות מורכבות יותר כמו הפיכת מתכת רגילה למוליך-על על ידי קירור מתחת לטמפרטורה מסוימת.

כאשר הטמפרטורה מתאפסת התנודות התרמיות פוסקות ולכן לא קיימים מעברי פאזה תרמיים. לעומת זאת, בטמפרטורת האפס המוחלט קיימות תנודות קוונטיות, הנובעות מעקרון האי-ודאות של הייזנברג, אשר, תחת תנאים מסוימים, עשויים לגרום למעברי פאזה הידועים כמעברי פאזה קוונטיים.

הגבול הקלאסי-קוונטי של מעברי פאזה

אף על פי שלא ניתן להגיע לאפס המוחלט, במערכות בטמפרטורה המתקרבת לאפס ניתן לזהות מאפיינים של מעברי פאזה באזור הנקודות הקריטיות. בטמפרטורות סופיות, התנודות התרמיות, שהן מסדר גודל של $k_{B}T$, כאשר $k_{B}$ הוא קבוע בולצמן, מתחרות עם התנודות הקוונטיות, שהן מסדר גודל של $\hbar \omega$, כאשר $\hbar$ הוא קבוע פלאנק המצומצם ו- $\omega$ היא התדירות הזוויתית האופיינית של התנודות הקוונטיות. בתחום הקלאסי, התנודות הקוונטיות זניחות ביחס לתנודות התרמיות. בתחום בו $\hbar \omega >k_{B}T$, התנודות הקוונטיות הופכות דומיננטיות. תחום זה נקרא התחום הקוונטי הקריטי.

איור 2: תחומי מעברי הפאזה הקלאסיים והקוונטיים. הנקודה על ציר P, בה הטמפרטורה שווה לאפס, מכונה נקודה קריטית קוונטית (באנגלית: Quantum Critical Point - QCP)

סדרים במעברי פאזה ואוניברסליות האקספוננטים הקריטיים

מעברי פאזה מסווגים למעברי פאזה מסדר ראשון, אם קיימת אי-רציפות בנגזרת הראשונה של האנרגיה החופשית, כפונקציה של המשתנה התרמודינמי בנקודת המעבר, בה שתי הפאזות מתקיימות במקביל, כדוגמת מים וקרח, ומעברי פאזה מסדר שני, אם קיימת אי-רציפות בנגזרת השנייה של האנרגיה החופשית, כפונקציה של המשתנה התרמודינמי ורציפות בנגזרת הראשונה בנקודת המעבר, בה שתי הפאזות לא יכולות להתקיים במקביל, כדוגמת פרומגנט בו המומנט המגנטי מתאפס מעל לטמפרטורה מסוימת. במעבר פאזה רציף, כלומר מסדר שני, נקודת המעבר נקראת הנקודה הקריטית והיא מאופיינת על ידי פרמטר סדר, שהוא משתנה תרמודינמי כלשהו המקבל ערך סופי בפאזה המאופיינת בסדר ומתאפס בפאזה המאופיינת באי-סדר. כמו מעברי פאזה קלאסיים, גם מעברי פאזה קוונטיים יכולים להיות מסר ראשון ומסדר שני.

נמצא כי במעברי פאזה קלאסיים מסדר שני, האקספוננטים הקריטיים הם אוניברסליים, כלומר, הם זהים עבור מעברי פאזות שונים במערכות פיזיקליות שונות. כדי ליצור אנלוגיה בין מעברי פאזה קלאסיים לקוונטיים נסתכל על דוגמה כללית:

ידוע כי מעברי הפאזה מתאפיינים בהתבדרות פרמטרים פיזיקליים של המערכת. מרחק הקורלציה, $\xi$, הוא דוגמה חשובה לפרמטר המתבדר בנקודה הקריטית כיוון שהוא קובע את סקאלת המרחק של ההתנהגות הקולקטיבית של המערכת בפאזה המסודרת. מרחק הקורלציה מתנהג לפי

$$\xi \thicksim |T-T_{c}|^{-\nu }$$

כאשר $T_{c}$ היא הטמפרטורה הקריטית ו- $\nu$ הוא האקספוננט הקריטי של מרחק הקורלציה. כעת נסתכל על המערכת הקוונטית המתוארת על ידי ההמילטוניאן $H(g)=H_{0}+gH_{1}$. פונקציית החלוקה של המערכת הקוונטית היא

$$Z=Tr(e^{-\beta H})$$

כאשר $\beta ={1 \over k_{B}T}$ . ערך תצפית של אופרטור קוונטי, $A$, נתון על ידי

$$\langle A\rangle ={1 \over Z}Tr(Ae^{-\beta H})$$

כיוון שהעקבה אינווריאנטית, אפשר להעריך אותה בהצגה כלשהי, ולכן פונקציית החלוקה ניתנת לכתיבה באופן הבא

$$Z=\sum _{\{\phi \}}\langle \{\phi \}|e^{-\beta H}|\{\phi \}\rangle$$

כאשר $|\{\phi \}\rangle$ זה סט שלם של מצבים. במכניקה קוונטית, לאופרטור, $e^{-\beta H}$, יש את הצורה של אופרטור ההתפתחות בזמן, כך ש- $t\rightarrow -i\beta$, לכן האופרטור, $e^{-\beta H}$, מקבל משמעות פיזיקלית בכך שהוא מקדם את המצב $|\{\phi \}\rangle$ בזמן מדומה $\beta$. אם כן, פונקציית החלוקה סוכמת את כל האמפליטודות, אלמנטי המטריצה, של כל ה"דרכים" שיובילו את המערכת בחזרה למצב המקורי, כלומר, תנאי שפה מחזוריים, בכיוון המדומה של הזמן, נכפים על ידי העקבה בפונקציית החלוקה. במעבר הפאזה, המערכת בגבול התרמודינמי, ממדי המערכת אינסופיים וכדי לוודא מעבר פאזה קוונטי ניקח את הטמפרטורה לאפס או, במילים אחרות, $\beta \rightarrow \infty$. בנקודה הקריטית הקוונטית, $g=g_{c}$, המערכת תציג התבדרות פרמטרים כמו במעבר הפאזה הקלאסי. לשם השוואה, אורך הקורלציה של המערכת מתבדר לפי

$$\xi \thicksim |g-g_{c}|^{-\nu }$$

בדומה לאורך הקורלציה במעברי פאזות קלאסיים. אך בשונה מהמעברים הקלאסיים, קיים גם "אורך" קורלציה בכיוון הזמן המדומה, $\xi _{\tau }$, שמתבדר לפי

$$\xi _{\tau }\thicksim |g-g_{c}|^{-\nu z}$$

כאשר $z$ הוא אקספוננט קריטי דינמי, שלא מופיע במעברים הקלאסיים כיוון שבמעברי פאזה תרמיים לא קיימת דינמיקה אינטרינזית.

מודלים תאורטיים למעברי פאזה קוונטיים

הפיזיקה המתארת את מעברי הפאזה הקוונטים היא מורכבת ולא מובנת לחלוטין, אך קיימים מספר מודלים תאורטיים פתירים הממחישים את החשיבות של מעברי פאזה קוונטים, ביניהם מודל איזינג הקוונטי, מודל הרוטור הקוונטי ומודל הובארד, לחלקם אף יישומים ניסויים.

מודל איזינג הקוונטי - דוגמה למעבר פאזה קוונטי

מודל איזינג הקוונטי מתואר על ידי ההמילטוניאן

$$H=-Jg\sum _{i}{\hat {\sigma _{i}^{x}}}-J\sum _{\langle {ij}\rangle }{\hat {\sigma _{i}^{z}}}{\hat {\sigma _{j}^{z}}}$$

כאשר $J>0$ הוא קבוע שחלוף הקובע את סקאלת האנרגיה המיקרוסקופית, ו- $g>0$ הוא קבוע צימוד חסר ממדים אשר ישמש לכיוון ההמילטוניאן אל מעבר הפאזה הקוונטי. דרגות החופש הקוונטיות של המערכת באות לידי ביטוי על ידי אופרטורי מטריצות פאולי ${\hat {\sigma _{i}^{\mu }}}$ (כאשר $\mu =x,z$) השוכנים באתרי סריג בעל $d$ ממדים ופועלות על מצבי הספין של האתר $i$. הסכום $\langle i,j\rangle$ הוא על שכנים קרובים $i,j$. הערכים העצמיים של אופרטורי מטריצות פאולי יסומנו $\sigma _{i}^{\mu }$ והם יכולים לקבל את הערכים $\pm 1$ עבור ספין במצב up $|\uparrow \rangle _{i}$ וספין במצב down $|\downarrow \rangle _{i}$. מצב היסוד של ההמילטוניאן תלוי בפרמטר הצימוד חסר הממדים, לכן נבחן כיצד משתנה המערכת בגבולות שונים של $g$:

• כאשר $g>>1$ האיבר הראשון בהמילטוניאן דומיננטי ולכן מצב היסוד הוא

$$|0\rangle =\prod _{i}(|\uparrow \rangle _{i}\pm |\downarrow \rangle _{i})/{\sqrt {2}}$$

כאשר אלו שני מצבים עצמיים של ${\hat {\sigma _{i}^{x}}}$ עם ערכים עצמיים $\pm 1$. הערכים של ${\hat {\sigma _{i}^{z}}}$ באתרים שונים חסרי קורלציה במצב היסוד הזה, לכן

$$\langle 0|{\hat {\sigma _{i}^{z}}}{\hat {\sigma _{j}^{z}}}|0\rangle =\delta _{ij}$$

תיקוני הפרעות ייצרו קורלציה ב- ${\hat {\sigma _{i}^{z}}}$ ועבור $g$ גדול מספיק נצפה לקורלציות קצרות-מרחק מהצורה

$$\langle 0|{\hat {\sigma _{i}^{z}}}{\hat {\sigma _{j}^{z}}}|0\rangle \thicksim e^{-|x_{i}-x_{j}|/\xi }$$

כאשר $x_{i}$ היא קואורדינטה מרחבית באתר $i$. עבור $|x_{i}-x_{j}|$ גדולים, מצב היסוד הוא אותו מצב יסוד עבור $g$ גדול ואורך הקורלציה $\xi$ הוא

$$\xi \thicksim |g-g_{c}|^{-\nu }$$

כפי שהוצג בפסקה הקודמת.

• כאשר $g<<1$ האיבר השני בהמילטוניאן דומיננטי. אם $g=0$, הספינים הם או למעלה או למטה. כאשר נגדיל במעט את $g$ ניצור ערבוב מצבים בחלק מהספינים בכיוונים מנוגדים, אך במערכת אינסופית, הניוון ישרוד עבור כל סדר סופי בתורת ההפרעות ב- $g$, כיוון שקיימת סימטריה גלובלית הממפה את מצבי היסוד אחד לשני. מערכת תרמודינמית תמיד תבחר מצב יסוד אחד על פני השני. מצב זה מכונה "שבירת סימטריה ספונטנית" של הסימטריה. התנהגות הקורלציה של ${\hat {\sigma _{i}^{z}}}$ היא

$$\lim _{|x_{i}-x_{j}|\rightarrow \infty }\langle 0|{\hat {\sigma _{i}^{z}}}{\hat {\sigma _{j}^{z}}}|0\rangle =N_{0}^{2}$$

איור 3: פיסה של מוליך על בטמפרטורה-גבוה bismuth strontium calcium copper oxide-BSCCO-2223 תיאורית מעבר הפאזה הקוונטית מספקת הסבר לתופעה.

כאשר $|0\rangle$ הוא אחד ממצבי היסוד ו- $N_{0}\neq 0$ היא המגנטיציה הספונטנית של מצב היסוד.

ערכי הקורלציה עבור שני תחומים לא יכולים להשתנות בצורה אנליטית כפונקציה של $g$. חייב להתקיים ערך קריטי $g=g_{c}$ בו פונקציות הקורלציה ישתנו אחת לשנייה - נקודה זו היא נקודת מעבר הפאזה הקוונטית.

יישומים

עד לפני מספר עשורים, נושא זה נחשב לתאורטי בלבד כיוון שבפועל לא ניתן להגיע לטמפרטורת האפס המוחלט, אך פיתוחים תאורטיים וניסויים שנעשו לאחרונה הראו כי קיום של נקודות קריטיות קוונטיות בטמפרטורת האפס המוחלט מסבירות תופעות שעד כה נחשבו לבעיות לא פתירות במערכות חומר מעובה רבות. דוגמאות לכך ניתן למצוא במוליכי-על-בטמפרטורות-גבוהות, יסודות מגנטים-מבודדים נדירים, תרכובות של פרמיונים כבדים וגז אלקטרונים דו ממדי.

ראו גם

• מעבר פאזה
• אקספוננטים קריטיים
• מודל איזינג
• מודל הובארד

לקריאה נוספת

• Subir Sachdev - "Quantum Phase Transitions"
• Lincoln D.carr - "Understanding Quantum Phase Transitions"
• Vladimir Dobrosavljevi´c, Nandini Trivedi, James M. Valles, Jr - "Conductor-Insulator Quantum Phase Transitions"
• Kaden Richard, Alan Hazzard - "Quantum Phase Transitions in Cold Atoms and Low Temperature Solids"

הערות שוליים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

22584448מעבר פאזה קוונטי