גל קפילרי

גל קפילרי (אדווה) במים.

גל קפילרי (בשפת היומיום: אַדוָוה; באנגלית: capillary wave או ripple) הוא גל מכני שמתקדם לאורך הגבול של פאזה נוזלית של זורם, אשר הדינמיקה ומהירות המופע שלו נשלטים על ידי אפקטים של מתח פנים.

גלים קפילריים נפוצים בטבע. אורך הגל של גלים קפילריים הוא באופן טיפוסי פחות מכמה סנטימטרים, ומהירות המופע שלהם לעולם אינה נופלת מ-0.2 מטרים לשנייה. גלים ארוכים יותר על פני השטח של זורם נקראים גלי כבידה-קפילריים ומושפעים הן על ידי אפקטים של מתח פנים, הן על ידי הכבידה, והן מהאינרציה של הזורם. באוקיינוס הפתוח, גלי ים גדולים בהרבה נוצרים לעיתים קרובות מההתקבצות של גלים קפילריים קטנים בהרבה אותם יצרה הרוח.

מהירותם של גלים קפילריים

יחס הנפיצה של גלים קפילריים המתקדמים בממשק שבין זורם בעל צפיפות ρ ומתח פנים σ לחומר אחר בעל צפיפות זניחה ביחס אליו, הינו:

$\omega ^{2}={\frac {\sigma }{\rho }}\,|k|^{3}$

כאשר ω היא התדירות הזוויתית ו-k הוא מספר הגל. מהירות המופע שמתקבלת היא:

$c_{p}={\frac {\omega }{k}}={\sqrt {\frac {\sigma k}{\rho }}}$

כלומר הגלים בעלי אורכי הגל הקצרים יותר מתקדמים מהר יותר.

גזירת הנוסחה

גלים קפילריים שנוצרים כתוצאה מנפילת טיפות מים על הממשק שבין מים לאוויר.

הרעיון המנחה בפיתוח הנוסחה למהירות ההתקדמות של גלים קפילריים הוא קבלת הביטוי לכוח המחזיר שפועל על אלמנט משטח של הזורם כתוצאה מהאפקט של מתח הפנים. בהתאם למשוואת יאנג-לפלס, הפרש הלחץ הקפילרי משני צידיו של ממשק זורם בעל עקמומיות ממוצעת שונה מאפס הוא יחסי למתח הפנים ולערך העקמומיות הממוצעת בנקודה המבוקשת. במקרה של גל קפילרי, ניתן להבין שאזורים שונים של הגל שרויים בעקמומיות שונה; דבר המקנה לאזורים שונים שונים של היריעה לחץ קפילרי שונה, כך שנוצרים כל העת הפרש לחצים שיוצרים כוחות המקדמים את הגל. כיוון שאנו מנתחים גל מישורי, העקמומיות בכיוון אחד של החזית מתאפסת, ורק העקמומיות בכיוון התקדמות הגל תורמת לעקמומיות הממוצעת. אם נניח עקמומיות לא גבוהה מדי של הגל, נקבל שהעקמומיות של חתך אורך של הגל שווה לנגזרת השנייה בכיוון האורכי של פונקציית הגל. בשפה מתמטית, נקבל את הביטוי הבא ללחץ הקפילרי בו אלמנט שטח שרוי:

$P(x)=\sigma f_{xx}(x,y,t)$.

משוואת יאנג-לפלס המיושמת לאלמנט שטח אינפיניטסימלי של פני המים מסייעת להבין את פילוג הלחצים בגל קפילרי.

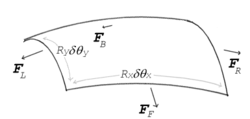
הצעד הבא בפיתוח נעוץ בתפיסת התקדמות הגל; הלחץ הרדיאלי בו שרוי כל אלמנט שטח של הזורם הוא תוצאה של הפעולה ההדדית של אלמנטי הזורם אחד על השני - הכוח האופקי שפועל על אלמנט זורם תיבתי שווה להפרש הכוחות האופקיים שיוצרים אלמנטי הזורם מימינו ומשמאלו. לפיכך נקבל, שהרכיב האופקי של הכוח המחזיר בנקודה פרופורציונלי לגרדיאנט העקמומיות לאורך הגל הקפילרי באותה נקודה. כלומר נקבל:

$F_{x,restoring}=\sigma f_{xxx}(x,y,t)dx\cdot dy\cdot dz$

מסת האלמנט התיבתי היא $\rho dx\cdot dy\cdot dz$. אם נחלק את פונקציית הכוח המחזיר האופקי במסת אלמנט הזורם, נקבל ביטוי מחזורי סינוסואידלי (שכן אנו מניחים תבנית גל של סינוס) לתאוצת האלמנט האופקית כפונקציה של הזמן, כלומר נקבל:

$a_{x}={\frac {F_{x,restoring}}{\rho dx\cdot dy\cdot dz}}=-{\frac {a\sigma k^{3}cos(kx-\omega t)}{\rho }}$.

כעת יש לשים לב שהתאוצה האנכית של הזורם נמצאת בהפרש מופע של $\pi /2$ עם התאוצה האופקית של הזורם, כך שבביטוי לתאוצה האנכית נקבל סינוס ולא קוסינוס:

$a_{y}=-{\frac {a\sigma k^{3}sin(kx-\omega t)}{\rho }}$

כצעד אחרון יש לקשור את המקדם $-{\frac {a\sigma k^{3}}{\rho }}$ של הסינוס לתדירות הזוויתית ω דרך הנגזרת הזמנית השנייה של פונקציית הגל:

$a_{y}=-{\omega }^{2}asin(kx-\omega t)$

מהשוואת שני הביטויים לתאוצה אנכית נקבל את יחס הנפיצה המבוקש:

${\omega }^{2}={\frac {\sigma k^{3}}{\rho }}$.

גלי כבידה-קפילריים

גרפם המסכמים את ההתנהגות של גלי כבידה-קפילריים.

הרעיונות המנחים בקבלת הביטוי למהירות גלים קפילריים יכולים לשמש להוספת תיקון ליחס הנפיצה של גלי כבידה במים עמוקים:

$\omega ={\sqrt {gk+{\frac {\sigma k^{3}}{\rho }}}}$.

ומהירות המופע היא:

$\omega /k={\sqrt {g/k+{\frac {\sigma k}{\rho }}}}$

ניתן לראות שהתלות של האפקט הקפילרי במספר הגל היא הפוכה מזו של האפקט הכבידתי - גלים קפילריים מתקדמים מהר יותר ככל שאורך הגל קצר יותר, לעומת גלי כבידה במים עמוקים שמתקדמים מהר יותר ככל שאורך הגל ארוך יותר. על כן נהוג להפריד בין שני "משטרים": התחום הכבידתי (גלים ארוכים) והתחום הקפילרי (גלים קצרים). בנוסף, מהירות המופע שבנוסחה האחרונה מקבלת מינימום באורך גל מסוים:

$\lambda _{min}=2\pi {\sqrt {\frac {\sigma }{\rho g}}}$

ומהירות המופע המינימלית היא:

$c_{min}={\sqrt {2{\sqrt {\frac {g\sigma }{\rho }}}}}$.

בעבור ממשק של מים ואוויר, אורך הגל λ_m הוא 1.7 סנטימטרים ומהירות המופע המינימלית c_m היא בערך 0.23 מטרים לשנייה.

ראו גם

• מתח פנים