Trie
| Trie | |||
|---|---|---|---|
 עץ trie אשר מכיל את המפתחות "A", "to", "tea", "ted", "ten", "i", "in" ו"inn". לכל אחת מהמחרוזות השלמות יש ערך שלם שרירותי שמקושר אליה. | |||
| יצירה | |||
| הומצא ב: | 1960 | ||
| ממציא: | אדוארד פרדקין, אקסל טו ורנה דה לה בריאנדייס | ||
| סיבוכיות מקום וזמן | |||
| |||
| זיכרון: |
| ||
| חיפוש: |
| ||
| הכנסה: |
| ||
| הוצאה: |
| ||
במדעי המחשב, trie, נקרא גם עץ קידומות או עץ דיגיטלי, הוא מבנה נתונים מסוג עץ אשר משמש לאיתור מפתחות מסוימים מתוך אוסף.
כמו שאר מבני הנתונים מבוססי החיפוש, ה-trie מאחסן מפתחות וערכים המקושרים אליהם. ברוב המקרים המפתח הוא מחרוזת, לעומת זאת הערך יכול להיות מכל סוג, לפעמים מדובר במזהה ייחודי או מצביע למידע הקשור למפתח הנ"ל. בשונה מעץ חיפוש בינארי, הצמתים במבנה לא מכילים מפתחות מאחר שהם מסמלים תו יחיד. במקום זאת, המיקום של צומת במבנה מגדיר את המפתח אליו הוא מקושר.
לכל "הילדים" של צומת מסוים יש את אותה קידומת של המחרוזת המקושרת עם צומת האב שלהם, בעוד השורש מקושר עם מחרוזת ריקה.
בדומה למילון, trie יכול גם לאחסן רק מפתחות ללא ערכים מקושרים.
היסטוריה
הרעיון ש-trie ייצג אוסף של מחרוזות תואר לראשונה באופן מופשט על ידי אקסל טו ב-1912. עצי trie הוזכרו לראשונה בקשר למחשבים על ידי רנה דה לה בריאנדייס ב-1959.
ב-1960 הרעיון פותח באופן עצמאי על ידי אדוארד פרדקין, שטבע את המושג trie, בעקבות ההברה האמצעית של המילה retrieval (שפירושה שליפה).
פעולות
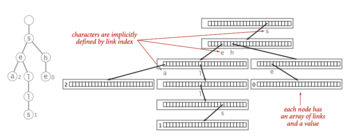
Trie תומך בפעולות: הכנסה, הוצאה וחיפוש אחר מחרוזת. ה-Trie מורכב מצמתים המכילים מערך בגודל מספר האיברים באלפבית. כל תא במערך מייצג סמל, ובהתאם מכיל קישור לצמתי המשך או ל- (ראו תמונה 2 להמחשה). מלבד השורש, על כל צומת מצביע צומת אחר, הקרוי "אב". ברוב המקרים, הגודל של מערך הילדים יהיה אורך הסיביות של קידוד התווים - לדוגמה 256 תאים במקרה של ASCII.
חיפוש
חיפוש אחר ערך בtrie מתבצע בעזרת התווים במחרוזת המפתח, כאשר כל צומת במבנה מכיל קישור תואם לכל תו אפשרי במחרוזת. לכן, מעקב אחר תווי המחרוזת בתוך הtrie יחזיר את הערך המקושר למחרוזת הקלט.
להלן מימוש החיפוש בפסאודו קוד בהינתן שורש של trie (x) ומחרוזת (key):
1 Trie-Find(x, key) 2 for 0 ≤ i < key.length do 3 if x.Children[key[i]] = nil then 4 return false 5 end if 6 x := x.Children[key[i]] 7 repeat 8 return x.Value
הכנסה
פעולת ההכנסה לtrie נעזרת במערכת התווים בתור אינדקסים של מערך "הילדים" עד הגעתה לתו האחרון של המחרוזת. למעשה, מבנה הtrie משקף ביצוע של מיון בסיס מתחילת המחרוזת לסופה.
להלן מימוש ההכנסה בפסאודו קוד בהינתן שורש של trie (x), מחרוזת (key) וערך (value):
1 Trie-Insert(x, key, value) 2 for 0 ≤ i < key.length do 3 if x.Children[key[i]] = nil then 4 x.Children[key[i]] := Node() 5 end if 6 x := x.Children[key[i]] 7 repeat 8 x.Value := value 9 x.Is-Terminal := True
במידה והאלגוריתם נתקל במצביע ל- לפני שהגיע לתו האחרון במחרוזת, הוא יוצר צומת חדש (כפי שניתן לראות בשורות 3–5).
הוצאה
הוצאה של מפתח-ערך מtrie מצריכה מציאה של צומת "סוף" בעזרת המחרוזת המקושרת אליו, שינוי סימון של אינדיקטור הסיום ל-false ושל הערך עצמו ל-.
להלן מימוש רקורסיבי לפעולת הוצאה של מחרוזת (key) מtrie (x):
1 Trie-Delete(x, key) 2 if key = nil then 3 if x.Is-Terminal = True then 4 x.Is-Terminal := False 5 x.Value := nil 6 end if 7 for 0 &le i &lg x.Children.length 8 if x.Children[i] != nil 9 return x 10 end if 11 repeat 12 return nil 13 end if 14 x.Children[key[0]] := Trie-Delete(x.Children[key[0]], key[1:]) 15 return x
הפעולה מתחילה בבדיקה האם חיפוש אחר המפתח הוביל לצומת "סוף" או לסיומה של מחרוזת. במידה ומדובר בצומת "סוף" ללא "ילדים", הצומת מוסר מה-trie. למרות זאת, הגעה לסיומה של מחרוזת מבלי שהצומת הוא צומת "סוף" מסמלת שהמחרוזת אינה קיימת ולכן לא מתבצע שום שינוי ב-trie. הרקורסיה מתקדמת על ידי קידום של אינדקס המפתח (שורה 14).
יישומים
מבני trie משמשים בדרך כלל עבור חיזוי מלל/השלמה אוטומטית ואלגוריתמים להתאמת מחרוזות משוערת. ה-trie מאפשר חיפושים מהירים ותופס יחסית מעט מקום, במיוחד כאשר המבנה מכיל מספר גדול של מחרוזות קצרות. לכן ה-trie נמצא בשימוש בבודקי איות, ביישומי מיקוף ובאלגוריתמים להתאמת הקידומת הארוכה ביותר.
מילוני מחרוזות יעילים גם בעיבוד שפה טבעית, כגון הוצאת לקסיקון מתוך אוסף של קובצי טקסט.
מיון
מיון לקסיקוגרפי של מחרוזות יכול להיות ממומש על ידי בניית trie עבור המחרוזות וסיור pre-order על העץ; למעשה זוהי דרך לבצע מיון בסיס. מבני ה-trie חשובים מאוד עבור Burstsort, אשר ידוע בשל היותו אלגוריתם מיון המחרוזות המהיר ביותר נכון לשנת 2007.
חיפוש טקסטים
גרסה מיוחדת של trie, שנקראת עץ סיפות, משמשת כדי לאנדקס את כל הסיומות האפשריות של טקסט מסוים ומאפשרת חיפוש וגישה מהירים אליהן.
מנועי חיפוש אינטרנטיים
גרסה מיוחדת של ה-trie, הנקראת trie דחוס, נמצאת בשימוש במנועי חיפוש אינטרנטיים כדי לאחסן את אוסף כל המילים הניתנות לחיפוש. כל צומת "סוף" מקושרת עם רשימת URL אשר מובילים לדפים שתואמים למילת המפתח.
ביואינפורמטיקה
ה-trie נמצא בשימוש בביואינפורמטיקה, במיוחד ביישומי עימוד רצפים כמו BLAST.
ניתוב אינטרנט
גרסאות דחוסות של trie נמצאות בשימוש לשם אחסון קידומות של כתובות IP בתוך נתבים וגשרים כדי לבצע חיפוש מבוסס קידומות.
קישורים חיצוניים
הערות שוליים
| מבני נתונים | ||
|---|---|---|
| מבנים מופשטים | רשימה • מחסנית • קבוצה • מולטי קבוצה • תור • דו-תור • תור עדיפויות • מילון • מחרוזת • איחוד קבוצות זרות | |
| מימושים ליניאריים | מערך • מערך משונן • טבלת גיבוב • רשימה מקושרת • רשימת דילוגים • חוצץ | |
| גרפים ועצים | ערימה (בינארית • בינומית • פיבונאצ'י) • עץ חיפוש (עץ אדום שחור • עץ 2-3 • עץ 2-3-4) • עץ סיפות • עץ B • עץ +B • עץ AVL • עץ Splay • עץ BSP • עץ kd • עץ R • Trie • X-fast trie • טריי y מהיר• עץ WAVL | |
| הסתברותיים | מסנן בלום | |
Trie35006292Q387015


