רשימה מקושרת
יש לערוך ערך זה. הסיבה היא: סגנון של ספר לימוד ולא אנציקלופדיה.
| ||
| יש לערוך ערך זה. הסיבה היא: סגנון של ספר לימוד ולא אנציקלופדיה. | |
| רשימה מקושרת | |||
|---|---|---|---|
|
רשימה מקושרת חד-כיוונית | |||
| סיבוכיות מקום וזמן | |||
| |||
| זיכרון: |
| ||
| חיפוש: |
| ||
| הכנסה: |
| ||
| הוצאה: |
| ||
| שליפה: |
| ||
רשימה מקושרת (אנגלית: Linked list) היא אחד ממבני הנתונים הבסיסיים ביותר הנמצאים בשימוש במדעי המחשב, כשמטרתה אחסון נתונים בצורה יעילה. הרשימה המקושרת היא אוסף איברים המפוזרים בזיכרון מחשב, בכל איבר מאוחסן מידע (אחד מאותם נתונים אותם רצינו לאחסן) וכן מצביע לאיבר הבא ברשימה. נקראת גם רשימה משורשרת. לעיתים קוראים לרשימה מקושרת בפשטות "הרשימה" על מנת לקצר.[1][2]
הגדרת רשימה מקושרת ופעולות בסיסיות
הקודים המופיעים מתחת לכל פעולה הינם פסאודו-קודים, וכתובים בשפה בעלת דמיון לשפה C.
הגדרה
הרשימה מכילה איברים, באנגלית Nodes. כל איבר מורכב משני אלמנטים:
- הנתון, data, זהו המידע איתו אנו עובדים ולשמו יצרנו את מבנה הנתונים.
- מצביע לאיבר הבא ברשימה next.
בנוסף, שומרים את מיקומו של האיבר הראשון ברשימה. דרך איבר זה ניתן להגיע לכל איברי הרשימה (דרך איבר זה ניתן להגיע לאיבר השני, דרכו ניתן להגיע לאיבר השלישי וכן הלאה).
struct List
{
Node firstNode // מצביע לאיבר הראשון ברשימה
}
מצביע יכול לקבל את הערך Null, ערך זה משמעותו שהמצביע אינו מצביע לשום מקום תקני בזיכרון. אם שדה ה-next באיבר מסוים מצביע ל-Null, משמעות הדבר שזהו האיבר האחרון ברשימה. אם השדה firstNode מצביע אל עבר Null, משמעות הדבר שהרשימה היא רשימה ריקה (רשימה שאין בה אף איבר).
הוספת איבר
עלינו לדעת תחילה היכן ברצוננו להכניס את האיבר החדש, ליתר דיוק, אחרי איזה איבר יבוא האיבר החדש. לשם פשטות, נניח שאנו רוצים להכניס איבר שנסמנו ב' בין שני איברים עוקבים שנסמנם א' ו-ג'. כעת תתבצע ההכנסה בשלושה שלבים פשוטים (יש לשים לב לכך שסדר הפעולות הוא משמעותי, אם נכוון קודם את מצביע א' אל מצביע ב', נאבד את הקשר בין איבר א' לאיבר ג', ובעצם לכל שאר הרשימה):
- צור את האיבר החדש, איבר ב'.
- כוון את מצביע האיבר ב' אל עבר איבר ג'.
- כוון את מצביע האיבר א' אל עבר האיבר ב'.
insert(Node node, Node newNode)
{
newNode.next <- node.next
node.next <- newNode
}
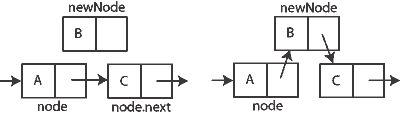
במקרה המיוחד בו ברצוננו להכניס את האיבר החדש לתחילת הרשימה, ובכך בעצם להופכו לאיבר הראשון, נצטרך לעדכן את המצביע firstNode, המורה מיהו האיבר הראשון ברשימה. כעת הליך ההכנסה יהיה:
- צור את האיבר החדש.
- כוון את מצביע האיבר החדש אל עבר האיבר הראשון הקיים, שיהפוך עכשיו לאיבר השני ברשימה.
- כוון את מצביע firstNode אל עבר האיבר החדש, שכעת יהיה האיבר הראשון ברשימה.
insertBeginning(List list, Node newNode)
{
newNode.next <- list.firstNode
list.firstNode <- newNode
}
הסרת איבר
ברצוננו להסיר איבר מסוים, נכנה את האיבר הבא אחריו ברשימה "האיבר הבא למוסר" ואת האיבר הקודם לו ברשימה "האיבר הקודם למוסר". כעת הליך ההסרה יתבצע בשני שלבים פשוטים:
- כוון את מצביע האיבר הקודם למוסר אל עבר האיבר הבא למוסר.
- מחק את האיבר שברצונך להסיר.
שים לב שרשימה מקושרת היא רשימת איברים כך שכל איבר מצביע לאיבר הבא אחריו. איבר שאף אחד לא מצביע אליו, אינו איבר באותה הרשימה. אין מונח של "חור" ברשימה, מרגע ששינינו את המצביע של האיבר הקודם למוסר, האיבר שרצינו להסיר נעלם מן הרשימה. השלב השני הוא למטרות ניקוי הזיכרון, מבחינה תאורטית מרגע שינוי המצביע, ההסרה בוצעה בהצלחה.
משום שברשימה מקושרת בגרסתה הקלאסית, אין באפשרותנו לחזור אחורה לאיבר הקודם, אין לנו דרך מהירה ויעילה לדעת מיהו האיבר הקודם למוסר. נעדיף להסתכל על ההליך כולו כהסרת איבר הבא אחרי איבר, כלומר, ידוע לנו מראש מיהו האיבר הקודם למוסר וכעת אנו רוצים להסיר את האיבר הבא אחריו. דרך הסתכלות זו איננה מהווה התחמקות מהבעיה, שכן בפעמים רבות באמת ידוע לנו מיהו האיבר הקודם למוסר מראש, אם בשל תכנון נכון של המערכת שבנינו או משום שהאלגוריתם בו אנו משתמשים מספק אותו.
removeAfter(Node node)
{
obsoleteNode <- node.next
node.next <- node.next.next
destroy obsoleteNode
}
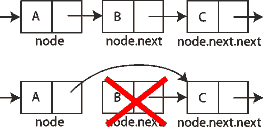
במקרה המיוחד בו נרצה למחוק את האיבר הראשון ברשימה, נצטרך לעדכן את המצביע firstNode, המורה מיהו האיבר הראשון ברשימה. כעת הליך ההסרה יהיה:
- כוון את firstNode אל האיבר הבא לאיבר הראשון.
- מחק את האיבר הראשון.
removeBeginning(List list)
{
obsoleteNode <- list.firstNode
list.firstNode <- list.firstNode.next
destroy obsoleteNode
}
יש להיזהר ממקרה של רשימה ריקה, מקרה בו firstNode מצביע אל עבר Null. כזכור, Null אינו באמת איבר ברשימה אלא רק סימון האומר שמצביע זה אינו מצביע על איבר ברשימה. ניסיון לגשת לשדה next ב-Null יוביל לתוצאות לא צפויות. נהוג להניח שפעולה זו לא נעשית על רשימה ריקה, כלומר, בעת תכנות עלייך לוודא שהרשימה אינה ריקה לפני ביצוע פעולה זו.
חיפוש איבר
כאשר אנו מדברים על חיפוש איבר ברשימה, אנחנו בעצם מתכוונים לחיפוש איבר המחזיק ערך מסוים. מה שמעניין אותנו הוא הערך ולא האיבר שכן, כפי שצוין קודם, מטרת האיבר היא בסך-הכל שמירה על הערך ומתן גישה נוחה אליו. אם כן, בהנחה שאנו מחפשים ערך_מבוקש יתנהל החיפוש בצורה הבאה:
- התחל מהאיבר הראשון ברשימה
- כל עוד האיבר אינו Null,
- אם ערך האיבר הוא ערך_מבוקש,
- החזר את האיבר
- עבור לאיבר הבא ברשימה
- אם ערך האיבר הוא ערך_מבוקש,
- החזר שערך_מבוקש אינו קיים ברשימה.
בעת מימוש הפעולה בפועל, יש לשים לב לכמה נקודות:
- עדיף שלא להגיע למצב בו אנו בודקים כעת את Null. הדבר עלול להביא לניסיון לגישה למקום Null בזיכרון, וזה בתורו יביא להתנהגות לא מוגדרת מצדו של המחשב. נעדיף לבדוק בכל פעם האם האיבר הבא איננו Null ורק במידה שאכן זה המצב, נתקדם אליו.
- במידה ואין ערבון לכך שערך_מבוקש אכן נמצא ברשימה, יש לטפל במקרה בו הוא לא נמצא. דרך אחת לעשות זאת היא החזרת ערך שלא ייתכן שהיה מוחזר לו היינו מוצאים את האיבר, Null משמש ערך טוב למטרות אלו, משום שלו היינו מוצאים את האיבר היינו מחזירים את מקומו בזיכרון ו-Null אינו מקום תקני בזיכרון.
- ניתן לתמצת את הקוד ולהכניס לתנאי הלולאה ("כל עוד...") גם את הבדיקה האם הערך הנוכחי הוא בעל הערך ערך_מבוקש. מצד שני, ניתן לבצע חיפושים מורכבים יותר, למשל לחפש את האיבר שערכו מקיים תנאים מסוימים כמו "ערכו של האיבר מתחלק בשמונה ללא שארית וגם האיבר הוא חזקה שלמה של 2", במקרה זה עדיף ולעיתים אף אין מנוס מלהשאיר את הבדיקות בגוף הלולאה.
search(List list, DataType data)
{
node <- list.firstNode
while node != Null
{
if node.data == data
return node
node <- node.next
}
return Null
}
מעבר סדרתי על איברי הרשימה
חיפוש איבר נעשה על ידי מעבר על כל האיברים עד אשר נמצא האיבר המתאים או שהגענו לסוף הרשימה. לעיתים לא נרצה להפסיק כאשר הגענו אל איבר מסוים, אלא נרצה להמשיך ולעבור על כל איברי הרשימה עד אשר הגענו לסופה. לרב, נרצה לבצע פעולות מסוימות על האיברים תוך כדי המעבר. ההליך יראה כך:
- התחל באיבר הראשון ברשימה
- כל עוד האיבר אינו Null,
- בצע את הפעילות המבוקשת על האיבר הנוכחי
- עבור לאיבר הבא ברשימה
function(List list, ...)
{
node <- list.firstNode
while node != null
{
(do something with node)
node <- node.next
}
}
שים לב לשלוש הנקודות (...) שהוכנסו לאחר הפרמטר הראשון בפונקציה לעיל, תלוי בפעילות הנדרשת על האיברים, הפונקציה עלולה להזדקק לפרמטרים שונים ואולי לא תזדקק כלל לאף פרמטר נוסף.
לרוב הפעולה על האיבר תהיה קשורה למידע השמור בו. למרות זאת, זהו לא תמיד המצב ולעיתים אף הנתון כלל לא יעניין אותנו. דוגמה לכך היא הפונקציה הבאה המקבלת רשימה מקושרת והופכת את סדר איבריה.
inverseList(List list)
{
node <- list.firstNode
newNext <- Null
while node != Null
{
tmp <- node.next
node.next <- newNext
newNext <- node
node <- tmp
}
list.firstNode <- newNext // האיבר הראשון ברשימה הוא מי שקודם לכן היה האחרון
}
תכונות הרשימה המקושרת
תכונתה הבולטת של הרשימה המקושרת היא העובדה כי האיברים אינם נמצאים ברצף בזיכרון המחשב, בניגוד למערך למשל. עובדה זו משמשת כחרב פיפיות שכן היא יתרונה וחסרונה הגדול של הרשימה המקושרת.
יתרונות
יתרונותיה הבולטים של הרשימה המקושרת הם בתחום הוספת איבר והוצאת איבר מן הרשימה.
יתרון גדול של הרשימה המקושרת בא לידי ביטוי דווקא ברשימות מקושרות בהן ישנה חשיבות לסדר האיברים (רשימה מקושרת ממוינת למשל). בעת הכנסת איבר אנו חייבים להכניסו במקום מדויק. עקב המבנה הייחודי של הרשימה המקושרת, כל שנצטרך לעשות יהיה להכניס את האיבר במקום כלשהו בזיכרון המחשב, לכוון את מצביעו אל עבר האיבר שברצוננו שיבוא אחריו ברשימה ולכוון את מצביע האיבר שברצוננו שיבוא לפניו, אל עברו. מדובר בשתי פעולות קבועות שאינן תלויות במספר איברי הרשימה ולכן נאמר שיעילות זמן הריצה היא .
הוצאת איבר תתבצע בצורה דומה. נכוון את המצביע של האיבר הקודם לזה שאנו מוציאים כך שיצביע על האיבר הבא ואז נמחק את האיבר. שוב מדובר בפעולות קבועות ללא תלות במספר איברי הרשימה המקושרת ולכן גם כאן יעילות זמן הריצה .
לא נצטרך באף אחד מהמקרים לטפל בשאר איברי הרשימה המקושרת שכן הסדר ביניהם נשמר! לא קיימת תופעה של "חורים" ברשימה המקושרת מכיוון שאין חשיבות למיקום אחסונם של האיברים, רק למצביעים.
עובדה זו היא יתרון גדול, בייחוד בהשוואה למבני נתונים כמו המערך בו נצטרך לסדר את האיברים לאחר הוצאת איבר מן האמצע, או לחלופין אם הוספנו יותר איברים ממה שציפינו, להקצות מקום חדש בזיכרון ולהעתיק אליו את כל האיברים הקיימים, פעולות הנמצאות בקשר לינארי (ישר) עם איברי המערך ולכן יעילות זמן ריצתם .
חסרונות
חסרונה הבולט של הרשימה המקושרת הוא בתחום הגישה לאיברים, או יותר נכון בתחום חיפוש האיברים.
עקב פיזור האיברים בכל רחבי זיכרון המחשב, כאשר נחפש איבר כלשהו נצטרך להתחיל מהאיבר הראשון ולהתקדם איבר אחד בכל פעם, עד אשר נגיע לאיבר המבוקש. כלומר, כל חיפוש יצרוך מאיתנו זמן ריצה . אפילו אם ברשותינו רשימה מקושרת ממויינת, לא נוכל להשתמש באלגוריתמי חיפוש מתוחכמים כמו שיטת החיפוש הבינארי (ידועה גם כשיטת האריה במדבר). גם אם נדע במדויק את מספרו של האיבר אותו אנו מחפשים, עדיין לא נוכל להתחמק ממעבר על כל האיברים עד איבר זה.
חסרון זה משמעותי ביותר. יש לזכור שלמרות שפעולת ההכנסה וההוצאה של איברים ברשימה מקושרת יעילות מאוד, לרוב לפני נצטרך למצוא את המיקום המתאים להכנסה (בדרך-כלל למצוא את האיבר שאחריו אנו רוצים להכניס) או את האיבר אותו ברצוננו להסיר ולצורך כך נצטרך לבצע חיפוש. אמנם פעולת ההוצאה או ההכנסה של האיבר יקחו רק , פעולת החיפוש תיקח וזמן ריצת התהליך כולו יסתכם ב-, בדיוק כפי שהיה לוקח לבצע פעולה דומה במערך.
חיסרון נוסף, אשר גם הוא קשור לעובדת היותם של האיברים מפוזרים בכל רחבי הזיכרון ובפרט הוא קשור להיעדר המקומיות (locality) הנובע מכך. כידוע, גישה לזיכרון היא פעולה יקרה יחסית מבחינת זמן ריצה. מסיבה זו, בין היתר, בעת בקשת מידע מהזיכרון, נהוג להביא יותר מידע ממה שנדרש מתוך הנחה שקיימת סבירות גבוהה שבקרוב נזדקק למידע הנמצא בקרבת מקום. זהו עקרון המקומיות. כאשר המידע מובא מהזיכרון, הוא נשמר בזיכרון המטמון והגישה למידע השמור שם מהירה הרבה יותר. את החיסרון בהיעדר המקומיות ניתן להרגיש בעת ביצועה של פעולה שכיחה למדי, סריקה סדרתית של אברי הרשימה. סדר גודל זמן הריצה של סריקת האיברים ברשימת מקושרת זהה לסדר גודל זמן הריצה של אותה הפעולה במערך - , ההבדל הוא שבעוד שבמערך בכל קריאה מהזיכרון יובאו מספר נתונים, משום שכל הנתונים שמורים ברצף בזיכרון, אין ערובה לכך שזהו המצב ברשימה ובהחלט ייתכן שהאיברים שמורים במקומות רחוקים זה מזה. בשל סיבה זו, בעוד שבמערך נזדקק לגשת בפועל לזיכרון רק לעיתים רחוקות (כל גישה לזיכרון תביא לזיכרון המטמון מספר איברים), ברשימה מקושרת אנו עלולים למצוא את עצמנו ניגשים ל-RAM עבור כל איבר ומבחינה מעשית זמן הריצה יגדל בעשרות מונים. חיסרון זה עשוי להתבטא באופן דומה, אך ביתר שאת, כאשר נעשה שימוש בזיכרון וירטואלי, שהגישה אליו איטית אף יותר מהגישה ל-RAM.
תוספות ושיפורים אפשריים
עוגן
לעיתים נרצה להגדיר איבר מיוחד בשם עוגן, שאת מקומו נדע מראש והוא יהיה האיבר הראשון ברשימה. באיבר זה לא ישמר מידע ויהיה בו רק מצביע לאיבר השני ברשימה. ללא שימוש בעוגן, יהיה עלינו לשמור מצביע אל האיבר הראשון ברשימה ולשנותו בכל פעם שזהותו של האיבר הראשון משתנה. לדוגמה, אם ברצוננו להוסיף איבר חדש שיהיה האיבר הראשון או לחלופין למחוק את האיבר הראשון, פעולה שתהפוך את האיבר השני לאיבר הראשון. הוספת העוגן מפשטת את הכנסת האיברים כי כך האיבר הראשון תמיד קבוע, לעולם לא נרצה למחוק אותו ולעולם לא נרצה להכניס איבר לפניו. יתרון זה בא לידי ביטוי בייחוד ברשימות בהן יש חשיבות לסדר האיברים, למשל רשימות ממויינות בהן אנו עלולים להכניס איבר שערכו קטן מערכם של כל איברי הרשימה ואז חייבים להכניסו בראש הרשימה.
רשימה מעגלית
רשימה מעגלית היא רשימה בה האיבר האחרון מצביע לאיבר הראשון. פתרון זה מאפשר בנית רשימה מקושרת באמצעות מבנה נתונים סטטי כך שגודל הרשימה אינו מוגבל על ידי גודל מבנה הנתונים והסיבוכיות אינה ניזוקה על ידי הצורך להזיז איברים בעת ההכנסה וההוצאה.
רשימה דו-כיוונית

ניתן להוסיף מצביע[3] אל האיבר הקודם ברשימה וכך תהפוך הרשימה לרשימה מקושרת (משורשרת) דו-כיוונית. ברשימה המקושרת הקלאסית, בה מצביע רק לאיבר הבא ברשימה, הגעה אל האיבר הקודם ברשימה מתבצעת על ידי סריקה סדרתית של הרשימה ולכל איבר בדיקה האם האיבר הבא אחריו הוא אותו איבר שאנו מעוניינים למצוא את הקודם לו. שיטה זו דורשת זמן ריצה מסדר גודל , אנו עלולים לעבור על כל איברי הרשימה בכל פעם. בצורה זו, נוכל להגיע אל איברים הקרובים יותר לסוף הרשימה תוך זמן מהיר יותר - אם ברצוננו להגיע לאיבר האחד לפני האחרון למשל, נוכל לעשות זאת תוך פעולה אחת, על ידי חזרה אחורה איבר אחד מהאיבר האחרון, שאנו שומרים מצביע אליו, כאשר בשיטה הרגילה נצטרך לעבור על כל האיברים מתחילת הרשימה.
קישורים חיצוניים
- מילון לאלגוריתמים ומבני נתונים.
הערות שוליים
- ↑ רשימה מקושרת, ספר מאת פרדריק פ. מילר, אגנס ואן דום וג'ון מקברוסטר
- ↑ הגדרת רשימה מקושרת
- ↑ לא חייבים להוסיף מצביע נוסף כדי לשדרג את הרשימה המקושרת ל"רשימה מקושרת דו-כיוונית". ניתן להשיג את אותו אפקט בעזרת מצביע בודד בשיטת רשימה מקושרת של XOR. בהתאם לנסיבות, שיטה זו אינה בהכרח יעילה יותר.
| מבני נתונים | ||
|---|---|---|
| מבנים מופשטים | רשימה • מחסנית • קבוצה • מולטי קבוצה • תור • דו-תור • תור עדיפויות • מילון • מחרוזת • איחוד קבוצות זרות | |
| מימושים ליניאריים | מערך • מערך משונן • טבלת גיבוב • רשימה מקושרת • רשימת דילוגים • חוצץ | |
| גרפים ועצים | ערימה (בינארית • בינומית • פיבונאצ'י) • עץ חיפוש (עץ אדום שחור • עץ 2-3 • עץ 2-3-4) • עץ סיפות • עץ B • עץ +B • עץ AVL • עץ Splay • עץ BSP • עץ kd • עץ R • Trie • X-fast trie • טריי y מהיר• עץ WAVL | |
| הסתברותיים | מסנן בלום | |

