ערימה בינארית

ערימה בינארית
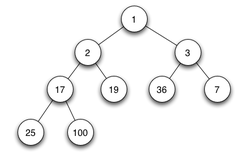דוגמה לערימת מינימום בינארית
סיבוכיות מקום וזמן
	ממוצע במקרה הגרוע
זיכרון:	O(n) O(n)
חיפוש:	O(n) O(n)
הכנסה:	O(1) O(log n)
הוצאה:	O(log(n)) O(log(n))
שליפה:	O(log n) O(log n)
הצצה:	O(1) O(1)

במדעי המחשב, ערימה בינארית היא סוג של מבנה הנתונים ערימה. יתרונה הגדול הוא בנוחות השימוש בה והמקום המועט הדרוש כדי לתחזק אותה.

הערימה משמשת בין השאר למיון המכונה מיון ערימה, ולמימוש מבנה הנתונים המופשט תור עדיפויות.

מבנה

הערימה מהווה עץ בינארי מלא, כלומר שכל השורות, פרט אולי לאחרונה, מלאות, והאחרונה מלאה משמאל עד לנקודה מסוימת. בנוסף, היא מקיימת את "כלל הערימה": כל ערך של צומת אינו גדול משני בניו (ערימה זאת מכונה "ערימת מינימום"; אפשרי גם שכל צומת אינו קטן משני בניו, ואז היא נקראת "ערימת מקסימום").

עם זאת, בפועל אין צורך לממש עץ בינארי: די להחזיק את האיברים במערך, כשהאיברים מסודרים בו משמאל לימין, שורה אחרי שורה, כאשר ידוע שאביו של איבר הנמצא במקום ה-i הוא $\lfloor {\frac {i-1}{2}}\rfloor$ ובניו נמצאים במקומות ה-$2i+1,2i+2$.

פעולות

עבור ערימת מינימום-

• הכנסה: כדי להכניס איבר חדש, מכניסים אותו בסוף הערימה, ולאחר מכן, כל עוד הוא קטן מאביו, מחליפים אותו עם אביו. סיבוכיות ריצה: $O(\log n)$ (הסבר על סימון זה). עם זאת, לפי רוברט פלואיד בשיטה מסוימת הסיבוכיות של בניית ערימה בת n איברים היא $O(n)$ בלבד.
• הוצאה: כדי להוציא איבר,מחליפים את האיבר המועד להוצאה באיבר האחרון במערך ומורידים את האיבר הנ"ל מסוף הרשימה. לאחר מכן כל עוד הוא גדול מבניו, מחליפים אותו בקטן שבבניו. סיבוכיות זמן ריצה: $O(\log n)$
• מציאת המינימום: מחזירים את האיבר הראשון. סיבוכיות זמן ריצה: $O(1)$.
• מחיקת המינימום: מוחקים את האיבר המינימלי, מעבירים את האיבר האחרון להתחלה, ולאחר מכן, כל עוד הוא לא קטן משני בניו, מחליפים אותו עם הקטן מביניהם. זמן ריצה: $O(\log n)$.
• הקטנת ערך: מקטינים ערך, ולאחר מכן, כל עוד הוא קטן מאביו, מחליפים אותו עם אביו. סיבוכיות זמן ריצה: $O(\log n)$.

בניגוד לערימה בינומית, ערימה בינארית לא תומכת במיזוג ערימות.

ערימה d-ארית

במקום לממש את הערימה כעץ בינארי, אפשר לממש אותה כעץ מכל דרגה אחרת. בערימה d-ארית לכל קודקוד d ילדים, ושאר המימוש בדומה. אביו של איבר הנמצא במקום ה-i הוא $\lfloor {\frac {i-1}{d}}\rfloor$ ובניו נמצאים במקומות ה- $di+1,di+2,...,di+d$. הכנסה והקטנת ערך יורדות ל-$O(\log _{d}n)$, ואילו מחיקת המינימום עולה ל-$O(d\log _{d}n)$ (משום שיש למצוא את הבן המינימלי).

שימושים

הערימה הבינארית משמשת למיון ערימה. במיון זה, בונים ערימה מהאיברים ולאחר מכן מוחקים אותם אחד אחד. יתרונו הוא שהוא לא דורש זיכרון נוסף, וזמן הריצה שלו הוא הטוב ביותר האפשרי: $O(n*logn)$ במקרה הגרוע.

קישורים חיצוניים

מדיה וקבצים בנושא ערימה בינארית בוויקישיתוף