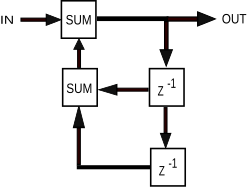
תגובת הלם אינסופית

תגובת הלם אינסופית ( IIR ) היא תכונה החלה על מערכות ליניאריות בלתי תלויה בזמן, אשר נבדלות בכך שיש להן תגובת הלם $h(t)$ שאינו מתאפס מעבר לנקודה מסוימת, אלא ממשיך ללא הגבלת זמן. זאת בניגוד למערכת תגובת הלם סופית (FIR) שבה תגובת הדחף אכן מתאפסת בזמן $t>T$ עבור $T$ סופי, ובכך בעל משך סופי. דוגמאות נפוצות למערכות ליניאריות בלתי תלויות בזמן הן רוב המסננים האלקטרוניים והדיגיטליים. מערכות עם תכונה זה ידועות כמערכות IIR או מסנני IIR .

בפועל, תגובת הדחף, אפילו של מערכות IIR, בדרך כלל מתקרבת לאפס וניתן להזניח אותה מעבר לנקודה מסוימת. עם זאת, המערכות הפיזיקליות המביאות לתגובות IIR או FIR אינן דומות, ובכך טמונה חשיבות ההבחנה. לדוגמה, מסננים אלקטרוניים אנלוגיים המורכבים מנגדים, קבלים ו/או משרנים (ואולי מגברים ליניאריים) הם בדרך כלל מסנני IIR. מצד שני, מסנני זמן דיסקרטיים (בדרך כלל מסננים דיגיטליים) המבוססים על קו השהייה מופעל ללא משוב הם בהכרח מסנני FIR. לקבלים (או למשרנים) בפילטר האנלוגי יש "זיכרון" ומצבם הפנימי אף פעם לא נרגע לחלוטין בעקבות דחף (בהנחה של המודל הקלאסי של קבלים ומשרנים שבו מתעלמים מהשפעות קוונטיות). אבל במקרה האחרון, לאחר שההלם הגיע לסוף קו ההשהיה שהופעל, למערכת אין זיכרון נוסף של אותו הלם והיא חוזרת למצבה ההתחלתי; תגובת ההלם שלו מעבר לנקודה הזו היא אפס בדיוק.

יישום ועיצוב

למרות שכמעט כל המסננים האלקטרוניים האנלוגיים הם IIR, מסננים דיגיטליים עשויים להיות IIR או FIR. הנוכחות של משוב בטופולוגיה של מסנן זמן דיסקרטי (כגון דיאגרמת הבלוק המוצגת להלן) יוצרת בדרך כלל תגובת IIR. פונקציית העברת של התמרת z של מסנן IIR מכילה מכנה לא טריוויאלי, המתאר את מונחי המשוב הללו. לפונקציית ההעברה של מסנן FIR, לעומת זאת, יש רק מונה כפי שמתבטא בצורה הכללית הנגזרת להלן. כל ה $a_{i}$ מקדמים עם $i>0$ (מונחי משוב) הם אפס ולמסנן אין קטבים סופיים.

פונקציות ההעברה הנוגעות למסננים אלקטרוניים אנלוגיים של IIR נחקרו בהרחבה ועברו אופטימיזציה עבור מאפייני המשרעת והפאזה שלהם. פונקציות סינון בזמן רציף אלו מתוארות בתחום Laplace . פתרונות רצויים יכולים להיות מועברים למקרה של מסנני זמן בדידים שפונקציות ההעברה שלהם מתבטאות בתחום z, באמצעות שימוש בטכניקות מתמטיות מסוימות כגון טרנספורמציה ביליניארית, איווריאנטיות דחפים או שיטת התאמת קוטב-אפס. לפיכך מסנני IIR דיגיטליים יכולים להתבסס על פתרונות ידועים עבור מסננים אנלוגיים כגון מסנן Chebyshev, מסנן Butterworth ומסנן אליפטי, שיורשים את המאפיינים של אותם פתרונות.

גזירת פונקציית העברה

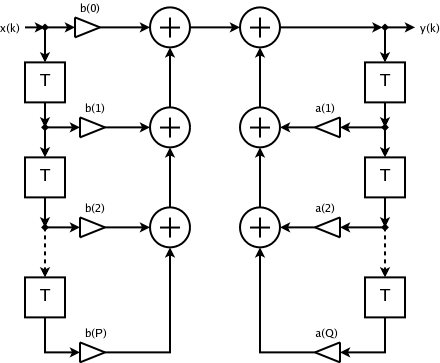
מסננים דיגיטליים מתוארים ומיושמים לעיתים קרובות במונחים של משוואת ההפרש המגדירה כיצד אות המוצא קשור לאות הקלט:

${\begin{aligned}y[n]{}=&{\frac {1}{a_{0}}}(b_{0}x[n]+b_{1}x[n-1]+\cdots +b_{P}x[n-P]\\&{}-a_{1}y[n-1]-a_{2}y[n-2]-\cdots -a_{Q}y[n-Q])\end{aligned}}$

כאשר:

• $\ P$ הוא סדר מסנן ההזנה
• $\ b_{i}$ הם מקדמי מסנן ההזנה קדימה
• $\ Q$ הוא סדר מסנן המשוב
• $\ a_{i}$ הם מקדמי מסנן המשוב
• $\ x[n]$ הוא אות הכניסה
• $\ y[n]$ הוא אות הפלט.

צורה אחרת של משוואת ההפרש היא:

$\ y[n]={\frac {1}{a_{0}}}\left(\sum _{i=0}^{P}b_{i}x[n-i]-\sum _{j=1}^{Q}a_{j}y[n-j]\right)$

שכאשר מסודר מחדש, הופך ל:

$\ \sum _{j=0}^{Q}a_{j}y[n-j]=\sum _{i=0}^{P}b_{i}x[n-i]$

כדי למצוא את פונקציית ההעברה של המסנן, ניקח תחילה את ה-Z-טרנספורמציה של כל צד של המשוואה שלעיל, כאשר אנו משתמשים בתכונה משמרת הזמן כדי לקבל:

$\ \sum _{j=0}^{Q}a_{j}z^{-j}Y(z)=\sum _{i=0}^{P}b_{i}z^{-i}X(z)$

אנו מגדירים את פונקציית ההעברה להיות:

${\begin{aligned}H(z)&={\frac {Y(z)}{X(z)}}\\&={\frac {\sum _{i=0}^{P}b_{i}z^{-i}}{\sum _{j=0}^{Q}a_{j}z^{-j}}}\end{aligned}}$

בהתחשב בכך שברוב עיצובי מסנן IIR מקדם $\ a_{0}$ הוא 1, פונקציית העברת מסנן IIR מקבלת את הצורה המסורתית יותר:

$H(z)={\frac {\sum _{i=0}^{P}b_{i}z^{-i}}{1+\sum _{j=1}^{Q}a_{j}z^{-j}}}$

דוגמה לתרשים בלוקים של מסנן IIR. בלוק ה $z^{-1}$ הוא השהיית יחידה.

יַצִיבוּת

פונקציית ההעברה מאפשרת להחליט האם מערכת היא יציבה עם קלט מוגבל, פלט מוגבל (BIBO) . ליתר דיוק, קריטריון היציבות של BIBO דורש שה- ROC של המערכת יכלול את מעגל היחידה. לדוגמה, עבור מערכת סיבתית, כל הקטבים של פונקציית ההעברה צריכים להיות בעלי ערך מוחלט הקטן מאחד. במילים אחרות, כל הקטבים חייבים להיות ממוקמים בתוך מעגל יחידה במישור z.

הקטבים מוגדרים כערכים של $z$ המגדירים את המכנה של $H(z)$ שווה ל-0:

$\ 0=\sum _{j=0}^{Q}a_{j}z^{-j}$

ניתן לראות כי כאשר $a_{j}\neq 0$ אז הקטבים אינם ממוקמים בראשית מישור ה-z. זאת בניגוד למסנן FIR בו כל הקטבים ממוקמים בראשית, ולכן הוא תמיד יציב.

מסנני IIR מועדפים לפעמים על פני מסנני FIR מכיוון שמסנן IIR יכול להשיג גלגול אזור מעבר חד הרבה יותר מאשר מסנן FIR באותו סדר.

דוגמה

תהא פונקציית העברה $H(z)$ של מסנן בזמן דיסקרטי מוגדרת על ידי:

$H(z)={\frac {B(z)}{A(z)}}={\frac {1}{1-az^{-1}}}$

נשלט על ידי הפרמטר $a$, מספר ממשי עם $0<|a|<1$ . $H(z)$ יציב וסיבתי עם קוטב ב $a$ . ניתן להראות שתגובת ההלם בתחום הזמן ניתנת על ידי:

$h(n)=a^{n}u(n)$

כאשר $u(n)$ היא פונקציית מדרגה. אפשר לראות ש $h(n)$ אינו אפס לכל $n\geq 0$, ובכך תגובת ההלם הנמשכת לאינסוף.

דוגמה למסנן IIR

יתרונות וחסרונות

היתרון העיקרי שיש למסנני IIR דיגיטליים על פני מסנני FIR הוא יעילותם ביישום, על מנת לעמוד במפרט מבחינת פס מעבר, פס חסימה, ריפל ו/או רול-אוף. ניתן להשיג קבוצה כזו של מפרטים עם מסנן IIR מסדר נמוך יותר ( Q בנוסחאות לעיל) ממה שנדרש עבור מסנן FIR העונה על אותן דרישות. אם מיושם במעבד אותות, הדבר מרמז על מספר קטן יותר של חישובים בכל שלב זמן; החיסכון החישובי הוא לרוב גורם גדול למדי.

מצד שני, מסנני FIR יכולים להיות קלים יותר לתכנון, למשל, כך שיתאימו לדרישת תגובת תדר מסוימת. זה נכון במיוחד כאשר הדרישה היא לא מהמקרים הרגילים (high-pass, low-pass, notch וכו') שנחקרו ועברו אופטימיזציה עבור מסננים אנלוגיים. כמו כן, ניתן להפוך את מסנני FIR בקלות לפאזה ליניארית ( השהיית קבוצה קבועה לעומת תדירות) - תכונה שלא ניתן לעמוד בה בקלות באמצעות מסנני IIR ולאחר מכן רק כקירוב (למשל עם מסנן Bessel ). סוגיה נוספת בנוגע למסנני IIR דיגיטליים היא הפוטנציאל להגביל התנהגות מחזורית במצב סרק, עקב מערכת המשוב בשילוב עם קוונטיזציה.

שיטות עיצוב

Impulse Invariance

Impulse Invariance היא טכניקה לתכנון מסנני תגובת הלם אינסופית (IIR) בזמן רציף שבהם נדגמת תגובת ההלם של מערכת הזמן הרציף כדי לייצר את תגובת הדחף של מערכת הזמן הבדיד.

Impulse Invariance היא אחת השיטות הנפוצות כדי לעמוד בשתי הדרישות הבסיסיות של המיפוי ממישור s למישור z. זה מתקבל על ידי פתרון ה-T(z) בעל אותו ערך פלט באותו זמן דגימה כמו המסנן האנלוגי, והוא ישים רק כאשר הכניסות נמצאות בפולס. חשוב לשים לב כי כל הכניסות של המסנן הדיגיטלי שנוצרו בשיטה זו הן ערכים משוערים, למעט כניסות פולסים מדויקות מאוד. זוהי שיטת עיצוב מסנן IIR הפשוטה ביותר. הוא המדויק ביותר בתדרים נמוכים, ולכן הוא משמש בדרך כלל במסננים נמוכים.

עבור טרנספורמציה של Laplace או Z-transform, הפלט לאחר ההמרה הוא רק הקלט כפול בפונקציית הטרנספורמציה המתאימה, T(s) או T(z). Y(s) ו-Y(z) הם הפלט המומר של קלט X(s) וקלט X(z), בהתאמה.

$Y(s)=T(s)X(s)$

$Y(z)=T(z)X(z)$

בעת הפעלת טרנספורמציה של Laplace או Z-transform על הלם היחידה, התוצאה היא 1. לפיכך, תוצאות הפלט לאחר ההמרה הן

$Y(s)=T(s)$

$Y(z)=T(z)$

כעת הפלט של המסנן האנלוגי הוא רק טרנספורמציה הפוכה של Laplace בתחום הזמן.

$y(t)=L^{-1}[Y(s)]=L^{-1}[T(s)]$

אם נשתמש ב-nT במקום t, נוכל לקבל את הפלט y(nT) הנגזר מהפולס בזמן הדגימה. זה יכול לנבוע לידי ביטוי גם כ-y(n)</br>

$y(n)=y(nT)=y(t)|_{t=sT}$

ניתן להחיל את אות הזמן הבדיד הזה כדי לקבל T(z)</br>

$T(z)=Y(z)=Z[y(n)]$

$T(z)=Z[y(n)]=Z[y(nT)]$

$T(z)=Z\left\{L^{-1}[T(s)]_{t=nT}\right\}$

המשוואה האחרונה מתארת מתמטית שמסנן IIR דיגיטלי אמור לבצע טרנספורמציה z על האות האנלוגי שנדגם והומר ל-T(s) על ידי Laplace, אשר בדרך כלל מפושט ל-</br>

$T(z)=Z[T(s)]*T$

שימו לב לעובדה שיש מכפיל T המופיע בנוסחה. הסיבה לכך היא שגם אם טרנספורמציה של Laplace ו-z-transform עבור דופק היחידה הם 1, הדופק עצמו אינו בהכרח זהה. עבור אותות אנלוגיים, לפולס יש ערך אינסופי אך השטח הוא 1 ב-t=0, אך הוא 1 בפולס בזמן הבדיד t=0, ולכן נדרש קיומו של מכפיל T.</br>

ראו גם

• דגם אוטורגרסיבי
• מסנן אלקטרוני
• תגובת הלם סופית
• נוסחת נסיגה, פורמליזציה מתמטית
• ניתוח מערכות

קישורים חיצוניים

מדיה וקבצים בנושא תגובת הלם אינסופית בוויקישיתוף

• (The fifth module of the BORES Signal Processing DSP course - Introduction to DSP] בארכיון Wayback Machine (אורכב 02.07.2016))
• (IIR Digital Filter Design Applet בארכיון Wayback Machine (אורכב 13.02.2010))
• IIR Digital Filter design tool - produces coefficients, graphs, poles, zeros, and C code
• EngineerJS Online IIR Design Tool - does not require Java

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

37718187תגובת הלם אינסופית