כלל המקבילית
כלל המקבילית הוא משפט בגאומטריה אוקלידית, הקובע כי סכום ריבועי ארבע צלעות המקבילית שווה לסכום ריבועי האלכסונים. במקרה שהמקבילית היא מלבן, האלכסונים שווים ומתקבל משפט פיתגורס. כלל המקבילית חל בכל מרחב מכפלה פנימית, ואף מאפיין את מרחבי המכפלה הפנימית בין כל המרחבים הנורמיים.
ניסוח וקטורי של כלל המקבילית
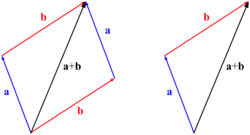
במישור האוקלידי, בהינתן שני וקטורים הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,a,b \ne 0} ניתן ליצור מקבילית שקודקודיה הם 0, ונקודות הקצה של הווקטורים a,b,a+b (ראו איור משמאל). אלכסוניה של המקבילית הם הווקטורים הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,a+b} ו-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,a-b} . כלל המקבילית קובע ש-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,2(|a|^2+|b|^2) = |a+b|^2+|a-b|^2} .
הכללה למרחבי מכפלה פנימית
בכל מרחב מכפלה פנימית הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ V} , לכל זוג וקטורים הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ z} ו-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ z'} מתקיים השוויון: הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ ||z+z'||^2 + ||z-z'||^2 =2 (||z||^2+||z'||^2) } כאשר
הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle ||x||^2 = \langle x, x\rangle} .
הכלל נובע מכך שהמכפלה הפנימית היא ביליניארית.
כלל המקבילית ומרחבים נורמים
כלל המקבילית מנוסח במונחי הנורמה המושרית במרחב מכפלה פנימית, ולכן אפשר לתהות באלו מרחבים נורמים הוא חל. מתברר שאם מרחב נורמי מקיים את כלל המקבילית, אז הנורמה שלו מושרית על ידי מכפלה פנימית.
להלן דוגמה למרחב נורמי שאינו מקיים את כלל המקבילית (ולכן אינו יכול להיות מושרה על ידי מכפלה פנימית). נסמן ב-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ L^{\infty}[0,1]} את מרחב הפונקציות הממשיות החסומות על הקטע [0,1], עם נורמת הסופרמום, הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,||f|| = \sup_{x\in [0,1]}|f(x)|} . בדרך זו הופך הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ L^{\infty}[0,1]} למרחב בנך. לפונקציות הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x) = x} ו-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(x) = 1-x} יש נורמה 1, ולכן הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,2(||f||^2+||g||^2) =2(1^2+1^2) =4} , בעוד ש-הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \,||f+g||^2 + ||f-g||^2 = 1^2 + 1^2 = 2} . כלל המקבילית אינו מתקיים, ולכן הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ L^{\infty}[0,1]} אינו מרחב מכפלה פנימית.
כלל המקבילית במרחבים מטריים כלליים
במרחב מטרי אין משמעות לחיבור או חיסור של נקודות, ובכל זאת אפשר לשמר גרסה מסוימת של כלל המקבילית. כדי לעשות זאת כראוי, נבחין שאת כלל המקבילית במרחב נורמי אפשר לנסח גם כך: הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ 4\left|\left|\frac{z+z'}{2}\right|\right|^2 + ||z-z'||^2 =2 (||z||^2+||z'||^2) } . כלומר, אם o היא נקודת האפס ו-x היא נקודת האמצע בין z ל-'z, אז הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ d(z,z')^2+4d(o,x)^2= 2d(o,z)^2+2d(o,z')^2} , כאשר d היא פונקציית המרחק המושרית על ידי הנורמה, הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ d(x,y) = ||x-y||} . מסיבה זו, אומרים שמרחב מטרי (X,d) מקיים את כלל המקבילית-למחצה אם לכל שתי נקודות הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ z,z' \in X} קיימת נקודה x, כך שלכל נקודה o מתקיים הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ d(z,z')^2+4d(o,x)^2 \leq 2d(o,z)^2+2d(o,z')^2} . במקרה זה, לכל הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ z,z'} הנקודה x היא נקודת האמצע (הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ d(z,x) = d(x,z')} ) היחידה בין הנקודות הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ z,z'} . מרחב מטרי שלם המקיים את כלל המקבילית-למחצה נקרא מרחב ברוה-טיץ. התכונה היסודית של מרחבים כאלה היא שכל קבוצה חסומה S מוכלת בכדור יחיד בעל רדיוס מינימלי; מרכז הכדור הזה הוא "מרכז המעגל החוסם" של S. מכאן נובע משפט נקודת השבת של ברוה-טיץ: אם לחבורת איזומטריות של מרחב ברוה-טיץ יש מסלול חסום, אז יש לה נקודת שבת.
קישורים חיצוניים
- כלל המקבילית, באתר MathWorld (באנגלית)
כלל המקבילית39450946Q919125