קו-מכפלה (תורת הקטגוריות)

במתמטיקה, ובמיוחד בתורת הקטגוריות, קו-מכפלה של אובייקטים בקטגוריה היא הכללה של בניות שונות במתמטיקה, כגון איחוד זר של קבוצות, מכפלה חופשית של חבורות, סכום ישר של מרחבים וקטוריים וכו'. במהותה, קו-מכפלה של זוג אובייקטים היא הקונספט הדואלי למכפלה (תורת הקטגוריות).

הגדרה

נניח כי C היא קטגוריה וכי $\,\{X_{j}|j\in I\}$ היא משפחה של אובייקטים ב-C. הקו-מכפלה של הקבוצה $\,\{X_{i}\}$ היא אובייקט X ביחד עם אוסף מורפיזמים $\,i_{j}:X_{j}\to X$ (הנקראות השיכונים הקנוניים, שהם לעיתים קרובות, אם כי לא תמיד מונומורפיזמים) אשר מקיימים את התכונה האוניברסלית הבאה: לכל אובייקט Y ואוסף מורפיזמים $\,f_{j}:X_{j}\to Y$ קיים מורפיזם יחיד $\,f:X\to Y$ כך שלכל $\,j\in I$ מתקיים $f_{j}=f\circ i_{j}$. במילים אחרות, לכל j הדיאגרמה הבאה היא דיאגרמה קומוטטיבית:

במילים אחרות, X הוא אובייקט התחלתי בקטגוריה ${}_{\{X_{j}\}}C=\left\{(Z,\{g_{j}:X_{j}\to Z\})\ |\ \forall i:X,X_{j}\in \mathrm {Ob} (C)\ ,\ g_{j}\in \mathrm {Mor} (Z,X_{j})\right\}$ עם המורפיזמים המתאימים (כך שהדיאגרמה המתאימה קומוטטיבית).

אם משפחת האובייקטים מכילה רק שני איברים, נהוג לסמן את המכפלה ב$\,X_{1}\coprod X_{2}$, ואז התכונה האוניברסלית מבוטאת על ידי הדיאגרמה הקומוטטיבית הבאה:

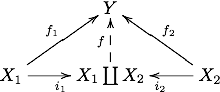
המורפיזם היחיד f ההופך את הדיאגרמה לקומוטטיבית מסומן לעיתים ב-f₁ ∐ f₂ או f₁ ⊕ f₂ או f₁ + f₂ או [f₁, f₂].

באופן כללי, הקו-מכפלה של $\,\{X_{j}|j\in I\}$ מסומנת

$X=\coprod _{j\in I}X_{j}$

ולעיתים

$X=\bigoplus _{j\in I}X_{j}$.

דוגמאות

• בקטגוריית הקבוצות, איחוד זר של קבוצות היא קו-מכפלה, כאשר השיכונים $i_{A}$ ו-$i_{B}$ הם פשוט ההכלות (כגון $A\subset A\uplus B$). בפרט, $A\coprod B=A\uplus B$, וזו הסיבה מדוע משתמשים לעיתים בסימן ∐ לציין איחוד זר.
• אפשר לבנות קו-מכפלה גם של קבוצות לא זרות באופן הבאה: אם $A\cap B\neq \emptyset$ לוקחים קבוצה $B'$ שוות עוצמה ל-B שזרה ל-A ואז בונים את האיחוד $A\uplus B'$ עם שיכון $i_{B'}\circ f$ כאשר $f:B\to B'$ היא פונקציית שקילות של קבוצות.
• קו-מכפלה בקטגוריה של חבורות אבליות היא סכום ישר של החבורות, ומסומנת $G\oplus H$.
• קו-מכפלה בקטגוריה של מרחבים וקטוריים היא סכום ישר של המרחבים, ומסומנת $V=\bigoplus _{j\in I}V_{j}$ כאשר את איבריה ניתן להציג כקבוצת כל הסכומים הסופים של איברים מ-V, כלומר: שכמעט לכל $j\in I$ האיבר שבא מ-$V_{j}$ שווה לאפס. למשל: $v_{1}+v_{2}\in \bigoplus _{n=1}^{\infty }V_{n}$ אך $0+0+v_{3}+v_{4}+v_{5}+...=\sum _{n=3}^{\infty }v_{j}\notin \bigoplus _{n=1}^{\infty }V_{n}$.
• בקטגוריה של חוגים קומוטטיביים עם יחידה, המכפלה הטנזורית של A ו-B הםומנת ב $A\otimes B$ היא קו-מכפלה, ביחד עם השיכונים הקנוניים $a\mapsto a\otimes 1\in A\otimes B$ ו-$b\mapsto 1\otimes b\in A\otimes B$.

קיום ויחידות

לא בכל קטגוריה C קיימת לכל משפחה $\,\{X_{j}\}$ קו-מכפלה. אם קיימת המכפלה אז היא יחידה במובן הבא: אם $\,i_{j}:X_{j}\to X$ ו-$\,i'_{j}:X_{j}\to X'$ הן זוג מכפלות של המשפחה $\,\{X_{j}\}$ אז קיים איזומורפיזם יחיד $\,f:X\to X'$ כך ש $i_{j}'=f\circ i_{j}$.

ראו גם

• מכפלה (תורת הקטגוריות)
• מכפלת סיב (תורת הקטגוריות)
• גבול ישר (תורת הקטגוריות)
• פונקטור מיוצג
• אובייקט התחלתי ואובייקט סופי