קורטה


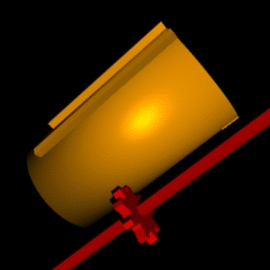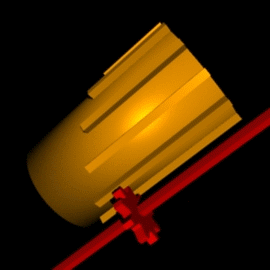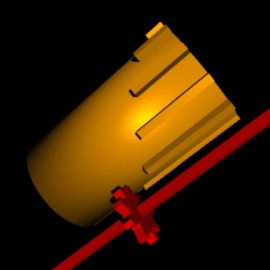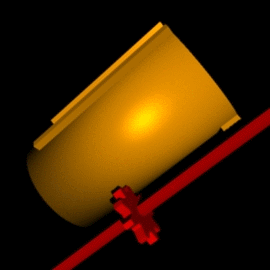
קוּרְטָה (Curta) הוא מכונת חישוב מכנית קטנה שיוצרה בין השנים 1949 ל-1971. זו מכונת החישוב המכנית הראשונה, ולמעשה היחידה, שיכולה להתכנות "מחשבון כיס". מכונות החישוב המכניות האחרות הן גדולות וכבדות בהרבה, וגודלן דומה לגודלה של מכונת כתיבה. המחשבון בנוי מצילינדר שמתאים לגודל כף היד. ניתן לבצע באמצעות המחשבון חיבור, חיסור, כפל, חילוק ואף הוצאת שורש ריבועי, ופעולות מתמטיות נוספות. הקורטה מבוסס על מנגנון "מחשב הפסיעות" של גוטפריד לייבניץ. הערכים נצברים על שיני גלגלי השיניים ומתווספים באמצעות מנגנון תוף פסיעה.
הממציא
 ערך מורחב – קורט הרצשטרק
ערך מורחב – קורט הרצשטרק
ממציא הקורטה הוא קורט הרצשטרק. אביו של קורט היה יצרן מכונות חישוב בווינה, אוסטריה, ובנו קורט נכנס לעסק בתחילת שנות ה-20 של המאה ה-20. הרצשטרק עסק גם במכירות ושירות, וגם בתכנון וייצור. הוא רשם את המצאתו הראשונה בתחום מכונות החישוב ב-1928, והמפעל המשיך למכור מכונות המבוססות על ההמצאה עד שהפסיק לייצר מכונות חישוב. במשך שנות השלושים של המאה העשרים, במקביל לעבודתו במפעל, ניסה הרצשטרק למצוא פתרון למכונת חישוב קטנה, מכונת כיס שתוכל לשרת אנשים כמו מהנדסים ומודדים שנמצאים בשטח, ואין ביכולתם לנסוע קילומטרים רבים עד למשרד עם מכונת חישוב שולחנית, ונאלצים להסתפק בפתרונות לא מספקים ולא מדויקים כמו סרגלי חישוב, או ביצוע חישובים עם נייר ועפרון. הרצשטרק פיתח את הרעיון הבסיסי בין 1937 ל-1938, ואפילו הספיק לבנות אבטיפוס עובד של המכונה, שהדגים את צורתה ואופן התפעול, אך עדיין לא פתר את כל האתגרים, והפונקציונליות שלו הייתה חלקית - האבטיפוס לא תמך בחיסור וחילוק, וידע לבצע חיבור וכפל בלבד. עד סוף 1938 כבר מצא הרצשטרק פתרונות לכל הבעיות, אך עקב האנשלוס של אוסטריה על ידי הנאצים, ומעבר המפעל לייצור ציוד עבור הוורמאכט, לא הספיק לייצר אבטיפוס של התיכון השלם.
אביו של קורט, שמואל, היה ממוצא יהודי, וב-1943 נעצר קורט ונשלח למחנה הריכוז בוכנוואלד. קורט שרד במחנה לאחר שהנאצים, שהיו מודעים היטב לכישוריו הטכניים, כמנהל מפעל שייצר ציוד עבור הוורמאכט, שלחו אותו לעבודת כפייה במפעל, דבר שלדבריו הציל את חייו. מפקדו מהאס אס למד על מכונת החישוב הקטנה שהרצשטרק מתכנן, אולי דרך מספר פטנטים על המכונה שהרצשטרק רשם ב-1937 וב-1938. המפקד אפשר לו להמשיך לעבוד על המצאתו אחרי שעות העבודה וביום ראשון בו היה המפעל סגור. הרצשטרק מספר שהמפקד אמר לו: "אם תצליח לבנות מכונה עובדת, אחרי הניצחון נעניק אותה במתנה לפיהרר, ואז בוודאי הוא יעשה אותך ארי".
בתנאים אלו השלים הרצשטרק את תכנון המכונה, ושירטט אותה על כל חלקיה, שירטוטים טכניים מדויקים עם מידות ואפילו אפיצויות. לאחר שחרור המחנה על ידי הצבא האמריקאי ב-1945, הצטרף הרצשטרק למפעל Rheinmetall בעיירה ויימאר הסמוכה לבוכנוואלד, והתברר שהשרטוטים שלו היו מלאים ומדויקים מספיק, עד כדי כך שתוך שמונה שבועות הצליח המפעל לייצר שלושה אבות טיפוס עובדים. שלא כמו האבטיפוס מ-1937, למכונות אלו כבר הייתה פונקציונליות מלאה, כמו הקורטה כפי שהיא היום, והן ביצעו חשבונות בצורה נכונה. אחרי שנחתם הסכם פוטסדאם ביולי 1945, התברר שוויימאר נמצאת בתחום ההשפעה הסובייטי, והחלו להגיע שמועות שהסובייטים לוקחים מדענים, מהנדסים, ואנשים עם כישורים טכניים ושולחים אותם לתוככי ברית המועצות, כנראה כדי לעזור לשקם את התעשייה הסובייטית (בעלות הברית המערביות נהגו באופן דומה, ושלחו מדענים וטכנאים, כמו מדעני הטילים לארצות הברית ואנגליה). הרצשטרק לא היה מעוניין להישלח, והחליט לחזור למשפחתו בווינה. הוא פירק את אבות הטיפוס וארז את החלקים, נטל את השרטוטים ונמלט לכיוון אוסטריה. אחרי קשיים והרפתקאות הצליח להתאחד עם משפחתו בווינה, שם החל לחפש מימון לייצור המצאתו. בסופו של דבר נוצר קשר עם נסיך ליכטנשטיין, וב-1946 החל הרצשטרק להקים את מפעל "קונטינה" בליכטנשטיין, לייצור המחשבונים. ב-1949 החל המפעל בייצור שוטף של מחשבונים, אך ב-1951 נוצר קרע בין הרצשטרק להנהלת המפעל, והוא פרש. המפעל המשיך לייצר מחשבוני קורטה, וב-1954 נוסף הדגם קורטה II, בעל תיכון זהה עקרונית, אבל עם יותר ספרות לקלט, מונה הסיבובים והתוצאה. הייצור נמשך עד 1971, ומכירת המכונות (כנראה מהמלאי) נמשכה עד 1973, ונפסקה עם הופעת מחשבוני כיס אלקטרוניים.
תיאור ושימוש
תיאור מנקודת ראותו של המשתמש

לקורטה יש מספר מנגנונים בעזרתם יכול המשתמש להזין מידע ("קלט"), וכמה דרכים לקרוא את תוצאת החישוב (פלט").
- קלט
- "צובר הקלט": צובר הקלט מוזן על ידי הזחת המחלקים הזחיחים על היקף המכונה מעלה ומטה: יש מחלק זחיח עבור כל ספרה (8 ספרות בקורטה I, ו-11 ב-II). את ערכו של צובר הקלט ניתן לקרוא בעזרת הספרות שמופיעות בהיקף מעל המחלקים
- ארכובה - סיבוב: הפעולה הבסיסית של הקורטה מתבצעת על ידי סיבוב הארכובה פעם אחת בכיוון השעון. בהקבלה למעבד, אפשר לומר שסיבוב אחד של הארכובה הוא "מחזור השעון" של הקורטה. הפעולה הבסיסית של הקורטה היא הוספת ערכו של צובר הקלט לצובר התוצאה. סיבוב הארכובה גם מקדם את "מונה הסיבובים".
- ארכובה - משיכה: ניתן למשוך את הארכובה כדי 3 מילימטר כלפי מעלה. כשעושים זאת, הפעולה הבסיסית מתהפכת: סיבוב הארכובה, במקום להוסיף את הקלט לתוצאה, מחסר מן התוצאה את ערך הקלט. במצב זה סיבוב הארכובה גם מחסר 1 ממונה הסיבובים במקום לקדם אותו ב-1.
- "עגלה": החלק העליון של הקורטה (מעל הספרות של צובר הקלט) נקרא "עגלה". המשתמש יכול למשוך את העגלה למעלה, כנגד קפיץ, ולסובב אותה לאחד מ-6 מצבים (8 מצבים בדגם II). כאשר מסובבים את העגלה, למשל למצב 2, המשמעות היא הכפלת צובר הקלט ב-10: אם ערכו של צובר הקלט הוא "12", סיבוב אחד של הארכובה יוסיף 12 לתוצאה כשהעגלה במצב "1", 120 כשהעגלה במצב "2", 1200 כשהעגלה במצב "3" וכן הלאה. כמו כן, כשהעגלה במצב "2" סיבוב הארכובה יוסיף למונה הסיבובים 10, ובמצב "3" - 100, וכן הלאה.
- איפוס: בחלקה העליון של העגלה, מתחת לארכובה, פנימה ממוני התוצאה והסיבובים, אפשר להבחין בתצלום בטבעת האיפוס, ובידית שלה, שמסתיימת בטבעת קטנה המתאימה לאצבע. על ידי סיבוב הטבעת סביב ציר הקורטה, ניתן לאפס את התוצאה או את מונה הסיבובים. שלא כמו הארכובה, את טבעת האיפוס אפשר לסובב בשני הכיוונים, ויש לה שתי נקודות "מצב מוצא" - בין הספרה האחרונה של התוצאה לראשונה של מונה הסיבובים, או בין האחרונה של מונה הסיבובים לראשונה של התוצאה. סיבוב הטבעת ממצב מוצא אחד לשני, מאפס את המונה מעליו עוברת הידית, וסיבוב מלא יאפס את שניהם. במצב עבודה רגיל הטבעת נעולה, וניתן לסובב אותה רק כאשר העגלה משוכה כלפי מעלה כנגד קפיץ, וההפך: רק כשטבעת האיפוס שבה לאחת משתי הנקודות של "מצב מוצא", העגלה יכולה לשוב מטה. הידית של טבעת האיפוס מתקפלת: במצב שימוש הידית משוכה החוצה, ולאחסון הקורטה בנרתיקה, יש לקפל את הידית.
- "היפוך". בחלקה האחורי של הקורטה, על פני הגליל בצד המנוגד לצובר הקלט, יש מחלק יחיד עם שני מצבים, המשמש להיפוך. במצב פעולה רגיל, סיבוב הארכובה מחבר את הקלט ומקדם את מונה הסיבובים, והעברה ל"חיסור" תגרום לכך שסיבוב הארכובה יחסר את הקלט מן התוצאה, וגם יחסר 1 ממונה הסיבובים. במצב "היפוך" מתהפכת התנהגותו של מונה הסיבובים: הוא מתקדם ב-1 דווקא כשהארכובה במצב "חיסור", וקטן ב-1 במצב חיבור. היפוך משמש בפעולות אריתמטיות שונות, כמו חילוק והוצאת שורש ריבועי.
- סמני נקודה עשרונית: בהיקף חלקה העליון של העגלה, ובהיקף הבסיס, יש טבעת שעליה מספר סמנים שאפשר למקם בין שתי ספרות בתוצאה, מונה הסיבובים או הקלט. לסמנים אין השפעה על פעולת הקורטה, והם נועדו לעזור למשתמש לזכור את מיקום הנקודה העשרונית כשמבצעים פעולות על שברים.
- פלט
- "'צובר התוצאה", זה הפלט העיקרי של הקורטה. בצובר התוצאה 11 ספרות בקורטה I, ו-15 ספרות ב-II. הצובר מוצג בספרות שנמצאות סביב ההיקף חלקה העליון של המכונה, ומוצג ברקע שחור. צובר זה מציג את התוצאה בפעולות חיבור, חיסור וכפל, ואת השארית בפעולת חילוק.
- מונה הסיבובים: המונה מראה את מספר הפעמים שהמשתמש סובב את הארכובה, בהתחשבות במצב העגלה: אם המשתמש סובב את הארכובה פעם אחת כשהעגלה במצב "1", פעם נוספת כשהעגלה ב-"2", ועוד פעמיים כשהעגלה ב-"3", יראה מונה הסיבובים 211. בסיום חישוב, המונה מראה את מספר המחוברים עבור פעולת חיבור, את הגורם השני במכפלה בפעולת כפל, ואת התוצאה בחילוק. בפעולת חיסור בדרך כלל יראה מונה הסיבובים 0. כמו התוצאה, גם מונה הסיבובים מוצג סביב ההיקף של חלקה העליון של המכונה, וכדי להבחין בינו ובין צובר התוצאה, הספרות של מונה הסיבובים מוצגות עם רקע בהיר. מצב ה"מנוחה" של טבעת האיפוס הוא באחד משתי נקודות: בין הספרה האחרונה של התוצאה לספרה הראשונה של מונה הסיבובים, או בין הספרה האחרונה של המונה לראשונה של התוצאה.
שימוש והפעלה
- חיבור: כדי לבצע חיבור, מאפסים את מונה הסיבובים ומונה התוצאה, מזינים את המחובר הראשון לצובר הקלט, על ידי הסטת הזחיחים מעלה ומטה, ומסובבים את הארובה פעם אחת. מזינים את המחובר הבא לצובר הקלט, ומסובבים שוב. חוזרים על הפעולה עבור כל המחוברים בפעולת החיבור. בסיום, צובר התוצאה מראה את הסכום, ומונה הסיבובים מראה את מספר המחוברים.
- חיסור: מאפסים את הצוברים, מזינים את המחוסר לקלט, ומסובבים פעם אחת את הארכובה. כעת המחוסר מופיע גם בקלט וגם בתוצאה, ומונה הסיבובים מראה "1". משנים את צובר הקלט למחסר, מושכים את הארכובה למצב "חיסור", ומסובבים פעם אחת. כעת התוצאה מראה את ההפרש, ומונה הסיבובים מראה "0".
- כפל: כדי לתאר כפל, ניעזר בדוגמה. נניח שעלינו לחשב $ 12345*123 $. כרגיל, בתחילת הפעולה מאפסים את מונה הסיבובים ואת צובר התוצאה. מזינים לצובר הקלט 12345. מסובבים את הארכובה 3 פעמים (כלומר שלוש יחידות). מונה הסיבובים יראה 3, והתוצאה תראה 12345*3. מקדמים את העגלה למצב "2" (עשרות), ומסובבים את הארכובה פעמיים (מונה הסיבובים יראה 23, כלומר 2 עשרות+3 יחידות). לסיום, מקדמים את העגלה ל-"3" (מאות), ומסובבים את הארכובה פעם אחת. בסיום הפעולה מונה הסיבובים יראה 123 (מאה אחת+2 עשרות+3 יחידות), ואוגר התוצאה מראה את המכפלה - 1518435. באופן כללי, בסיום פעולת כפל, הגורם הראשון מופיע בצובר הקלט, והגורם השני במונה הסיבובים, מה שמאפשר למשתמש לוודא שלא עשה טעות. בזכות המעבר הפשוט בין חיסור לחיבור, קל יחסית לתקן טעויות: אם מסובבים את הארכובה סיבוב מיותר, מונה הסיבובים מראה את הטעות, והתיקון מתבצע על ידי משיכת הארכובה ל"חיסור" וסיבובה.
לעיתים אפשר למצוא קיצורים: בספרון ההפעלה של קורטה מופיעה הדוגמה הבאה: כדי לכפול את הקלט ב-89, יש לסובב את הארכובה 9 פעמים כשהעגלה במצב "1", ועוד 8 פעמים כשהעגלה ב-"2" - בסך הכל 17 פעמים. אפשר, במקום זאת, להתחיל כשהעגלה במצב "3" ולסובב את הארכובה פעם אחת. כדי לכפול ב-100, ואז למשוך את הארכובה למצב חיסור, ולסובב פעם אחת כשהעגלה במצב "2", ועוד פעם במצב "1", וכך לחסר מהגורם השני 11, כדי לקבל 89. באופן זה כפל ב-89 מצריך שלושה סיבובים של הארכובה, במקום 17. - חילוק: מארבע פעולות החשבון, פעולת החילוק היא המסובכת ביותר להסבר. יש יותר מדרך אחת לבצע חילוק. אחת הדרכים היא כדלקמן: מאפסים את הצוברים, מזינים את המחולק (כלומר ה"מונה" בפעולת החילוק) לקלט, מסובבים פעם אחת, ומאפסים את מונה הסיבובים והקלט (אך לא את התוצאה!). כעת מופיע המחלק בתוצאה, ו-0 במונה הסיבובים. מעבירים את מחלק ה"היפוך" למצב היפוך, מזינים לקלט את המחלק (ה"מכנה"), ומושכים את הארכובה למצב חיסור. מזיזים את העגלה להיסט המרבי בו הקלט עדיין קטן מהתוצאה, ומסובבים את הארכובה עד שהתוצאה קטנה מהקלט. מסובבים את העגלה עד שהקלט שוב קטן מהתוצאה ושוב מסובבים עד שהתוצאה קטנה מהקלט. בסיום הפעולה, מונה הסיבובים מראה את התוצאה, וצובר התוצאה מראה את השארית. כדי לקבל דיוק טוב יותר, מכפילים את המחולק בחזקה של 10: למשל אם נרצה לחלק 12 ב-7 בשיטה שתוארה, נקבל תוצאה 1 ושארית 5. אם לעומת זאת נזין מלכתחילה 12,000, נקבל 1714 ושארית 2. שימוש בסמני הנקודה העשרונית יראה שהתוצאה היא 1.714.
- איפוס: אפשר לאפס את צובר התוצאה ואת מונה הסיבובים באופן עצמאי. האיפוס מתבצע על ידי משיכת העגלה כלפי מעלה, כנגד קפיץ, וסיבוב ידית האיפוס. שלא כמו הארכובה, שניתנת לסיבוב בכיוון אחד בלבד (עם כיוון השעון), ידית האיפוס יכולה להסתובב בשני הכיוונים. הידית נחה בין מונה הסיבובים לצובר התוצאה.
קיימים אלגוריתמים נוספים, ברמות סיבוך שונות, שמאפשרים לחשב בעזרת הקורטה שורש ריבועי, ועוד תוצאות שונות[1].
מבנה פנימי
רקע
ברמה הבסיסית ביותר, מנגנון הקורטה מבוסס על מכונת חישוב בשם "אריתמומטר", שהומצאה כ-130 שנים קודם לכן, ב-1820, ויוצרה באופן תעשייתי ונמכרה באופן מסחרי החל מ-1850. האריתמומטר עצמו, מבוסס על המצאה של המתמטיקאי בן המאה ה-17, גוטפריד וילהלם לייבניץ, בשם "תוף מדורג" או "תוף פסיעה", שמודגם באנימציה משמאל. באריתמומטר, יש תוף וגלגל שיניים עבור כל ספרה. סיבוב הארכובה מסובב את כל התופים של כל הספרות, וחיסור מתבצע על ידי סיבוב הארכובה בכיוון השני.
האריתמומטר שטוח, שלא כמו הקורטה, וה"עגלה" באריתמומטר, שנמצאת בחלקו העליון, נעה באופן קווי ימינה ושמאלה, בדומה לעגלה של מכונת כתיבה (זה גם מקור הכינוי "עגלה").
אחד המנגנונים שמוסיפים סיבוך הוא מנגנון ה"נשא" (Carry): למשל, כשמחברים 9 ל-3: החיבור מתבצע על ידי הזחת גלגל השיניים למצב "9" וסיבוב התוף. אחרי סיבוב אחד של התוף, גלגל השיניים במצב "9". כעת מזיחים את גלגל השיניים למצב "3" מול התוף, ומסובבים שוב. הגלגל מתקדם ב-3 שיניים, ועובר מ-9, דרך ה-0 עד ל-2. נחוץ מנגנון שיוסיף 1 לספרה שמשמאל (בדוגמה זו - ספרת העשרות), כשהגלגל של ספרת האחדות עובר מ-9 ל-0. בביצוע פעולת חיסור, המנגנון פועל בצורה שונה במקצת.
קורטה עושה זאת קצת אחרת
ממציא הקורטה, קורט הרצשטרק, הוסיף מספר שכלולים והמצאות לתיכון האריתמומטר. השכלול הראשון הוא שימוש בתוף יחיד עבור כל הספרות במקום תוף נפרד לכל ספרה. זה מתאפשר בעזרת סידור גלגלי השיניים של הספרות באופן מעגלי סביב התוף במקום באופן קווי כמו באריתמומטר. שכלול זה מאפשר כמובן חיסכון משמעותי במקום ומשקל.
השכלול הבא נוגע לאופן ביצוע החיסור: בגלל הסיבוך של מנגנון ה"נשא", ממציא הקורטה לא מצא בהתחלה פתרון לחיסור, ואכן האבטיפוס הראשון של ה"קורטה", שנבנה ב-1937 או 1938 לא ידע לבצע חיסור, אלא חיבור וכפל בלבד. בהברקה שלפי דברי הממציא, קורט הרצשטרק, הופיעה כשישב בקרון רכבת בחזרה מנסיעת שיווק לאזור היער השחור, הוא הבין שניתן לבצע חיסור בעזרת חיבור המשלים.
רעיונות דומים הופיעו כמה עשרות שנים מוקדם יותר, כפטנטים ואפילו כמכונות ממש, ובפרט, הממציא השוודי אקסל יקוב פטרסון (Axel Jacob Petersson) בנה ב-1875 מכונת חישוב גלילית לפי עקרונות דומים[2], ויותר מכך בעבודותיו של הממציא הגרמני קריסטל המן (Christel Hamann): הרעיון של מבנה גלילי, תוף מדורג יחיד לכל הספרות, ובוררים אנכיים מופיע בפטנט מ-1902[3], (שנת לידתו של הרצשטרק), ומומש בצורה שונה במקצת על ידי המן במוצר בשם "גאוס" ב-1905 (השנה בה פתח אביו של הרצשטרק את המפעל הראשון שלו)[4]. המן גם בנה מכונות חישוב ("המן מאנוס[5]) שהשתמשה בעיקרון "המשלים ל-10" לצורך ביצוע חיסור. קרוב לוודאי שהרצשטרק הכיר את עבודתו של המן, אם כי אולי לא את עבודתו של פטרסון.
- חיסור בעזרת חיבור המשלים
במכונות חישוב מכניות אין מספרים שליליים, אבל בגלל שיש מספר סופי של ספרות, יש "משלים": למשל, במכונת חישוב עם 4 ספרות, חיבור 9999 ל-1 ייתן 0, משום שספרת האלפים היא האחרונה, וכשהיא עוברת מ-9 ל-0, אין לאן להעביר את ה"נשא". המשמעות היא שבמכונה כזו אפשר לחסר 1 ממספר בעזרת חיבור 9999, ובדומה אפשר לחסר כל מספר אחר בעזרת חיבור המשלים המתאים. אפשר להשיג את המשלים בלי לשנות את ההזחה של גלגלי השיניים על ידי שימוש בתוף "הפוך", כלומר תוף כזה שבמיקום שמתאים לספרה "0" מכיל 9 בליטות, כך שגלגל השיניים יסתובב 9 פעמים, ובמיקום המתאים ל-"7" יש 2 בליטות. באופן כזה מוחלף המספר במשלים ל-9999 (מספר הספרות "9" כמספר הספרות במכונה). מכיוון שכדי לבצע חיבור צריך את המשלים ל-10,000 ולא ל-9999, צריך, בנוסף להחלפת התוף, להוסיף בסיום הפעולה 1. הרצשטרק המציא דרך לבצע את חיבור ה-"1" הנוסף במחיר של הוספת גלגל שיניים יחיד, ועוד פרוסה בתוף.
- שני תופים בתוף אחד
אפשר לתאר את התוף במכונת "קורטה", באופן סכמטי, כך:
- לוקחים שני תופים, אחד כמו באיור ואחד הפוך (כלומר כך שכשגלגל השיניים במצב השמאלי ביותר, שבתוף שבאיור משמעו "0", הגלגל יסתובב כדי 9 פסיעות וההפך: במצב הימני ביותר, בו התוף באיור יסובב את גלגל השיניים כדי 9 פסיעות, בתוף ה"הפוך" גלגל השיניים לא יתקדם כלל).
- פורסים כל אחד משני התופים לעשר פרוסות, ובונים תוף חדש, בו נוטלים לסירוגין פרוסה מכל תוף. בתוף החדש, המרחק בין ספרה לספרה הוא כעובי שתי פרוסות, ולעומת זאת הזחת גלגל השיניים כדי עובי פרוסה אחת, מעביר בין ספרה למשלים ל-9 של אותה הספרה.
בפועל, התוף של הקורטה מסובך קצת יותר, (בין השאר כדי לתמוך בהוספת ה-1 האחרון בסיום פעולת החיסור, כפי שתואר למעלה), ומורכב מ-39 פרוסות שונות, עם מספר שונה של שיניים בכל פרוסה, בין 0 ל-9. משיכת הארכובה החוצה מושכת עמה את התוף, באופן שמול גלגלי השיניים נמצא המשלים: למשל, כשהמשתמש מזיח את המחלק של ספרת האחדות ל-3, הפעולה מציבה את גלגל השיניים מול פרוסה בתוף שיש עליה 3 שיניים, כך שסיבוב הארכובה יקדם את האחדות ב-3. משיכת הארכובה (והתוף), מציבה מול גלגל השיניים פרוסה שעליה 6 שיניים, כלומר המשלים ל-9 של 3, וסיבוב הארכובה יקדם את האחדות ב-6.
מעל התוף וגלגלי השיניים נמצא מנגנון ה"נשא", שאחראי לקדם את הספרה הבאה משמאל כאשר ספרה מקודמת מ-9 ל-0. החלק המרכזי במנגנון זה מכונה "פעמון העשרות" (במכונות חישוב שולחניות, כאשר יש נשא לספרה העליונה שאין לאן להעבירו, המכונה משמיעה צלצול פעמון, בדומה לפעמון של מכונת כתיבה, כדי שהמשתמש ידע שארעה גלישת חוצץ. ייתכן שזה מקור השם "פעמון העשרות", למרות שבקורטה אין פעמון כזה). בנוסף ל"פעמון העשרות" מנגנון הנשא מורכב מגלגלי שיניים נוספים, וכן מ"מוטות נשא", שמזיחים את גלגל השיניים של הספרה הבאה אל מול פרוסה בתוף עם שן יחידה.
באופן זה, הקורטה מבצעת חיבור, חיסור, חילוק וכפל, למרות שהמנגנון המכני שלה יודע לעשות דבר אחד בלבד: חיבור.
בנוסף להמצאות שתוארו עד כאן, מכילה הקורטה מנגנונים רבים נוספים, שעל חלקם נרשמו פטנטים, ותפקידם למנוע שגיאות של המשתמש שיגרמו לנזק למכונה או לתוצאה שגויה. להלן רשימה חלקית של שכלולים אלו. הרבה מהמנגנונים מיועד למנוע פעולות שונות כאשר הארכובה לא נמצאת בעמדת המוצא שלה.
- אי אפשר לסובב את הארכובה בכיוון הלא נכון (נגד כיוון השעון)
- אי אפשר להעביר את העגלה ממצב למצב אלא אם כן היא משוכה החוצה
- אי אפשר לסובב את טבעת האיפוס, אלא אם כן העגלה משוכה החוצה
- אי אפשר למשוך את העגלה החוצה כאשר הארכובה לא בעמדת המוצא (ולכן לא ניתן גם לסובב את ידית האיפוס או לשנות את מצב העגלה)
- לא ניתן לסובב את הארכובה כאשר העגלה משוכה החוצה
- אפשר להעביר את הארכובה בין מצב "חיבור" למצב "חיסור" רק כשהארכובה נמצאת בעמדת המוצא
- אי אפשר לסובב את הארכובה כאשר היא משוכה החוצה באופן חלקי - כדי לסובב אותה היא צריכה להיות לגמרי במצב חיבור או חיסור
- משיכת הארכובה למצב "חיסור" חושפת "צווארון" בצבע אדום בולט סביב בסיס הארכובה, כך שהמשתמש רואה בצורה ברורה ובולטת שהמכונה במצב "חיסור" (בדגמים ישנים יותר, צבע הצווארון לבן ולא אדום) כדי למנוע טעות הפעלה של חיסור במקום חיבור, או ההפך.
- מנגנון שנועל את הספרות של התוצאה ומונה הסיבובים כאשר הארכובה נמצאת בעמדת המוצא. מנגנון זה מאפשר להשתמש בקורטה גם בסביבה מרובת טלטולים או רעידות, בלי להסתכן באפשרות שטלטלה חזקה תשנה את התוצאה על ידי הזזת אחת או כמה מהספרות
- מספר רב של מנגנונים שמיועדים לוודא שחלקי המכונה נמצאים במצב מוגדר, ולא בין שני מצבים. הרבה מהמנגנונים הללו ממומשים בעזרת קפיץ שלוחץ גולת מתכת לגומה, או למרווח בין שיני גלגל שיניים.
כאמור, הרשימה הזו היא חלקית, ובקורטה יש מנגנונים נוספים שתפקידם למנוע טעויות של המשתמש, נזק למכונה, או תוצאה שגויה. אנקדוטה קטנה נוגעת לקופסה של הקורטה: כיוון שהארכובה מסתובבת בכיוון השעון, התברר שיכול לקרות לפעמים שאחסון הקורטה בקופסה וסגירת המכסה, מסובבת במקצת את הארכובה ומוציאה אותה מ"עמדת המוצא", וכך, כשמוציאים את הקורטה מן הקופסה בפעם הבאה, היא לא מוכנה לשימוש. כדי לפתור את הבעיה הזו, שונה מבנה הקופסה, כך שהיא נסגרת על ידי סיבוב בכיוון ההפוך, נגד כיוון השעון, והמנגנון הקיים שמונע מהארכובה להסתובב בכיוון ההפוך מבטיח שסגירת הקופסה לא תוציא את הארכובה מעמדת המוצא.
קורטה טיפוס 1 וטיפוס 2
לקורטה טיפוס 1 היו 8 זחלנים, אחד לכל ספרה, מונה סיבובים בן 6 ספרות, ומונה תוצאה בן 11 ספרות. הקורטה טיפוס 2 היה בעל ממדים גדולים יותר. הוא הושק בשנת 1954 והיו לו 11 זחלנים (11 ספרות), מונה סיבובים בן 8 ספרות ומונה תוצאה בן 15 ספרות. מספרם המוערך של מחשבוני קורטה שיוצרו, עומד על כ-140,000 (80,000 מטיפוס 1, 60,000 מטיפוס 2). הקורטה האחרון יוצר בשנת 1970.
יציבות ואמינות
מחשבון הקורטה יוצר במשך יותר מ-20 שנה (דגם II יוצר במשך כ-17 שנים), ובמהלך התקופה לא חל בו כל שינוי משמעותי, וכמעט לא חלו שינויים כלל. השינוי המשמעותי ביותר היה החלפת החלק החיצוני של מחלקי הקלט: המחשבונים הראשונים יוצרו עם בליטה גלילית, אך אחרי זמן לא רב הוחלף העיצוב למחלק מלבני, שחלקו החיצוני מעוגל ומחורץ (התמונות מראות את העיצוב המלבני). הבדלים קטנים נוספים קשורים בטבעת האיפוס ובידית האיפוס: אחת התקלות שהתרחשו היא שבירת ידית האיפוס, כתוצאה מנפילת המחשבון, או משום שהמשתמש שכח לקפל את הידית לפני הכנסת המחשבון לקופסה וסגירתה. כדי להקל את השירות, שונה במקצת המנגנון כל שבדגמים מאוחרים יותר ניתן להחליף את הידית בלי צורך לפרק את הקורטה. פרט לשינויים אלו, ועוד מספר שינויים זעירים, המחשבון האחרון שיצא מהמפעל ב-1971 זהה למעשה למחשבונים הראשונים שיוצרו ב-1949.
הקורטה הוא מכשיר מכני שלמרות הסיבוך הניכר במבנהו (מודל I בנוי מכ-630 חלקים, מהם 139 חלקים שונים זה מזה. מודל II בנוי ממעט יותר חלקים), עקב החומרים המשובחים, הדיוק בייצור, והתכנון הקפדני, אמינותו גבוהה ביותר, והוא ממשיך לתפקד גם בתנאי סביבה קשים. פחות מ-3% מהמחשבונים שיוצרו הוחזרו לבית החרושת לתיקונים, כשחלק מאלו שהוחזרו, "סבלו" מכך שהמשתמשים רצו לראות איך המחשבון פועל ופרקו אותו, אך לא הצליחו להרכיבו בחזרה.
שימוש במרוצי מכוניות
הקורטה היה פופולרי בקרב מתחרים במרוצי מכוניות בשנות ה-60, ה-70 וה-80 של המאה ה-20. הכוונה למרוצים מסוג ראלי, בהם יושב לצג הנהג משתתף נוסף, בדרך כלל בתפקיד נווט. נווטים רבים השתמשו במחשבוני קורטה לצורך חישובים שונים, שעזרו להם להדריך את הנהג, למשל כדי לחשב מהירות ממוצעת לסיבוב. אפילו לאחר הצגת המחשבון האלקטרוני המתקדם יותר, עדיין עשו בקורטה שימוש לחישוב זמנים לנקודות ביקורת, מרחקים וכו', בזכות אמינותו ויכולתו להמשיך לפעול גם בתנאי סביבה קשים. מתחרים אשר עשו שימוש במחשבונים כאלה כונו "ארכובאי-הקורטה" על ידי אלו שהגבילו עצמם לנייר ועפרון, או אלה שעשו שימוש במחשבים שחוברו לגלגלי המכונית.
בימינו

במשך כ-22 שנים, בין 1949 ו-1971 יוצרו במפעל קונטינה כ-140,000 מחשבוני קורטה משני הדגמים, עם מעט מאד שינויים במשך השנים. בזכות האיכות הגבוהה והדיוק של הייצור, הרבה מאד מהמחשבונים הללו עדיין מתפקדים בצורה מושלמת. יש אספנים רבים שאוספים מחשבוני קורטה, ומתקיים מסחר ער במחשבוני קורטה באתרים כמו eBay, ובבתי מכירה פומבית. מחשבון קורטה נמכר בארצות הברית בשנות ה-60 של המאה העשרים ב-$125 עבור דגם I, ו-$165 לדגם II. היום נמכרים המחשבונים במחירים בין כ-$500 עבור מחשבונים "פשוטים", ועד מספר אלפי דולרים עבור מחשבונים מיוחדים, למשל כאלו עם מספר סידורי נמוך. מכונות מבוקשות במיוחד הן כאלו בהן מחלקי הקלט בצורה הישנה, של גלילים קצרים, כמו באבטיפוסים, ומכונות שמכסה קופסתן מתברג בכיוון השעון לסגירה. בנוסף למכונות עצמן, אספנים סוחרים בפריטים נוספים הקשורים בקורטה, כמו האריזה המקורית, חוברת ההוראות למשתמש, וספרונים וחוברות שחברת קונטינה הוציאה ומלמדים לבצע בעזרת הקורטה פעולות שונות בתחומים שונים כמו מדע, סטטיסטיקה, הנהלת חשבונות ועוד. אספנים גם מעוניינים במוצרים נלווים, כמו פוסטר המפרט את חלקי המכונה, בול המוקדש לה, ועוד.
מספר מומחים במדינות שונות (ביניהן איטליה, שווייצריה, גרמניה, וארצות הברית) מתקנים ומשפצים מכונות קורטה, בעזרת חלקי חילוף מקוריים שהמפעל סיפק, חלקים שהתקבלו מפירוק מכונות שיצאו מהמחזור, ובעת מצוק חלקים שהמשפץ מייצר בעצמו, כשם שעדיין ניתן למצוא שענים שיודעים לתקן שעונים מכניים.
חברת קונטינה ייצרה מספר קטן של "ערכות הדגמה" - ערכה כזו כוללת מחשבון קורטה חתוך, באופן שמאפשר לראות את הפעולה הפנימית, למרות שהמחשבון עדיין מתפקד, ומספר חלקים פנימיים בקופסה מהודרת. הערכה מיועדת לסוכני ונציגי מכירות, כדי לעזור להסביר על פעולת הקורטה. ערכות אלו נסחרות כיום במחירים של הרבה אלפים, עד כדי עשרות אלפי דולרים.
מלכות ליכטנשטיין החלה להכיר בייחוד של הקורטה, הקימה מוזיאון המוקדש בחלקו או ברובו לקורטה (המוזיאון הזה מחזיק כמה מהאבטיפוסים המוקדמים, כולל אחד או שניים מאלו שיוצרו ב-Rheinmetall ב-1945), ובשנת 2006 אף הוציאה בול שמוקדש למחשבון הקורטה.
מוזיאונים
מחשבון הקורטה זכה להכרה כאבן דרך משמעותית, הן בהקשר של מכונות חישוב מכניות, והן בהקשר של עיצוב תעשייתי. מוזיאונים רבים בעולם מציגים את הקורטה כחלק מהתצוגה הקבועה שלהם, ורבים אחרים מציגים אותה בתערוכות מתחלפות. להלן רשימה חלקית של מוזיאונים שמציגים קורטה. רשימה מלאה יותר מופיעה באתר שמוקדש ברובו לקורטה, כאן.
- מוזיאון היסטוריית המחשב בקליפורניה [1]
- המוזיאון הגרמני (מינכן) [2]
- Arithmeum בבון, גרמניה (מוזיאון המוקדש ברובו למכונות חישוב)
- מוזיאון היינץ ניקסדורף, בפדרבורן, גרמניה [3]
- המוזיאון לאמנויות ולמקצועות בפריז
- מוזיאון המחשוב בסווינדון, בריטניה
- מוזיאון המדע ברדבורי, בלוס אלמוס, ניו מקסיקו
- המוזיאון הלאומי לטכנולוגיה בפראג, צ'כיה [4]
- "המוזיאון הלאומי למחשוב" בבלצ'לי פארק, בריטניה
קישורים חיצוניים
- Erwin Tomash, ראיון עם קורט הרצשטרק, באתר מכון צ'ארלס בבג' של אוניברסיטת מינסוטה, 10 ו-11 בספטמבר 1987 (באנגלית)
- פעילות לקהל הרחב במוזיאון המדע בירושלים - דצמבר 2006 התערוכה "מסע בין חישובים"
- סיפורו המדהים של מחשבון הכיס הראשון מאת קליף סטול, סיינטיפיק אמריקן, ינואר 2004
- סימולציה של קורטה
- Curta.Org, האתר השלם למחשבון הקורטה
- חוברת התפעול של הקורטה
- אתר הקורטה מאת גרג סבילה
- הקורטה המדהימה מאת ברוס פלם
- כיצד יש לערוך חישובים באמצעות קורטה
- נישאי הקורטה במוזיאון מחשבוני HP
- קורט הרצשטרק ומחשבון הקורטה
- YACS - Yet Another Curta Simulator
- Type & Age of your Curta
- אתר המוקדש למחשבוני קורטה ולמחשבוני HP. באתר חומר רב ומגוון ממקורות שונים.
הערות שוליים
- ↑ Contina AG, Vaduz, Computing examples for the Curta calculating machine, חוברת הדרכה לשימוש בקורטה, עם אלגוריתמים שונים לחילוק, שורש ריבועי, שורש מעוקב, חישובים חשבונאיים וסטטיסטיים שונים, ועוד., לא ידוע (באנגלית)
- ↑ תצלום המכונה של פטרסון במוזאון הטכני בסטוקהולם
- ↑ הפטנט של המן מ-1902, שמתאר מכונה דומה להפתיע לקורטה. לא ידוע על מכונה ממשית שנבנתה לפי פטנט זה
- ↑ מכונת החישוב "גאוס" במוזאון הטכני בסטוקהולם
- ↑
 Haman Manus R - The Missing Link, בביצוע 1stSpyGuy, סרטון באתר יוטיוב: הדגמת מכונת החישוב המן-מנוס שמדגימה את השימוש במשלים ל-10 לצורך ביצוע חיסור. המכונה בסרטון היא דגם R מ-1950, אבל מכונות המן מנוס השתמשו בעיקרון זה החל מ-.1925
Haman Manus R - The Missing Link, בביצוע 1stSpyGuy, סרטון באתר יוטיוב: הדגמת מכונת החישוב המן-מנוס שמדגימה את השימוש במשלים ל-10 לצורך ביצוע חיסור. המכונה בסרטון היא דגם R מ-1950, אבל מכונות המן מנוס השתמשו בעיקרון זה החל מ-.1925