ספירלה לוגריתמית

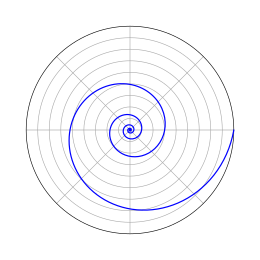
ספירלה לוגריתמית (זווית גידול 10°).

ספירלה לוגריתמית, שנקראת גם ספירלה שוות-זווית, היא עקום ספירלי בעל דמיון עצמי אשר מופיע במקומות רבים בטבע. הספירלה הלוגריתמית תוארה לראשונה על ידי דקארט ונחקרה לעומק מאוחר יותר על ידי יאקוב ברנולי, שכינה אותה Spira mirabilis - "הספירלה המופלאה".

הגדרה

בקואורדינטות פולריות $(r,\theta )$ העקום הלוגריתמי ניתן לכתיבה כך:

$r=ae^{b\theta }\,$

כאשר e הוא בסיס הלוגריתם הטבעי ו-$a$ ו-$b$ הם קבועים ממשיים חיוביים שרירותיים.

לספירלה הזאת יש את התכונה שהזווית $\phi$ בין המשיק לספירלה בנקודה $(r,\theta )$ לקו הרדיאלי המחבר בין הראשית לנקודה היא קבועה. תכונה זאת ניתנת לביטוי כך:

$\arccos {\frac {\langle \mathbf {r} (\theta ),\mathbf {r} '(\theta )\rangle }{\|\mathbf {r} (\theta )\|\|\mathbf {r} '(\theta )\|}}=\arctan {\frac {1}{b}}=\phi .$

הנגזרת של $\mathbf {r} (\theta )$ פרופורציונלית לפרמטר $b$. במילים אחרות, פרמטר זה מכתיב את קצב הגידול של הספירלה. במקרה הקיצון בו $b=0$ (כלומר כאשר $\textstyle \phi ={\frac {\pi }{2}}$), הספירלה הופכת למעגל בעל רדיוס $a$. לעומת זאת, בגבול בו $b$ שואף לאינסוף (ו-$\phi \rightarrow 0$) הספירלה מתנוונת והופכת לחצי קו ישר העובר דרך הראשית. הערך המוחלט של הזווית המשלימה ל-90 מעלות של $\phi$ נקראת זווית הגידול (pitch angle) של הספירלה.

"הספירלה המופלאה" ויאקוב ברנולי

Spira mirabilis, התרגום הלטיני לספירלה המופלאה, הוא שם אחר לספירלה הלוגריתמית. אף על פי ששם זה כבר ניתן לעקום זה על ידי מתמטיקאים אחרים, השם המסוים (ספירלה "פלאית" או "מופלאה") הזה ניתן לעקום הזה על ידי יאקוב ברנולי, שהוקסם מאחת מתכונותיה המתמטיות הייחודיות של הספירלה: כאשר מגדילים את הספירלה פי גורם כלשהו הצורה שלה נותרת ללא שינוי, תכונה שידועה כעת כדמיון עצמי. קרוב מאוד לוודאי שהודות לתכונה ייחודית זאת הספירלה התפתחה בטבע, ומופיעה בתצורות גדילה שונות כגון בקונכיות של הנאוטילוסיים ובראשי חמניות. יאקוב ברנולי ביקש שספירלה כזאת תיחרט על מצבתו יחד עם הכתובית "Eadem mutata resurgo" ("אף על פי שאשתנה, אחזור מחדש זהה"), אולם, בטעות, ספירלת ארכימדס נחרטה שם במקום.

תכונות

הספירלה הלוגריתמית מובחנת בקלות מהספירלה הארכימדית באמצעות העובדה שהמרחקים בין שתי פניות עוקבות של הספירלה הלוגריתמית גדלים באופן גאומטרי, בעוד שבספירלה הארכימדית המרחקים הללו קבועים.

ספירות לוגריתמיות דומות לעצמן בכך שהתוצאה של ההפעלה של כל קינום על הספירלה נותנת ספירלה שחופפת לספירלה המקורית. שינוי סדר גודל של הספירלה בפקטור $e^{2\pi b}$, כאשר b הוא הפרמטר מההגדרה של הספירלה, וכאשר מרכז הקינום הוא בראשית, נותן את אותו עקום כמו העקום המקורי; זאת בעוד שינויי סדר גודל אחרים נותנים עקום ספירלי זהה אך מסובב ביחס לעמדה המקורית של הספירלה. בכך מתבטאת תכונתה הייחודית של הספירלה הלוגריתמית: הפעלת קינום עליה כמוה כהפעלת פעולת סיבוב על הספירלה, או בניסוח אחר, לכל פעולת קינום של הספירלה קיימת פעולת סיבוב כך שהפעלת שתי הפעולות בזו אחר זו על הספירלה נותנת את העקום המקורי. גם האוולוט (העקום המורכב מאוסף כל מרכזי העקמומיות של הספירלה) של הספירלה הלוגריתמית הוא ספירלה לוגריתמית; אם משוואת הספירלה המקורית היא $r=e^{b\theta }$ אז משוואת האוולוט שלו היא $r=Abe^{b\theta }$ כאשר $A=e^{-b\pi /4}$.

כשמתחילים מנקודה $P$ ונעים פנימה לאורך הספירלה, ניתן להקיף את הראשית אינסוף פעמים מבלי להגיע אליה; ובכל זאת, המרחק הכולל על הנתיב הזה הוא סופי; כלומר, הגבול של האורך כאשר $\theta$ שואף ל-$-\infty$ הוא סופי. הראשון שהבחין בכך היה אוונג'ליסטה טוריצ'לי, עוד לפני שהחשבון האינפיניטסימלי הומצא. המרחק הכולל שמכוסה בהליכה מנקודה $P$ לראשית הוא $\textstyle {\frac {r}{\cos(\phi )}}$ כאשר $r$ הוא אורך הקו הישר מ-$P$ לראשית.

הפונקציה האקספוננציאלית של משתנה מרוכב x ממפה במדויק את כל הקווים ישרים הלא מקבילים במישור המרוכב (כלומר כאשר נקודה על הישר נלקחת כמספר מרוכב) לכל הספירלות הלוגריתמיות במישור המרוכב עם ראשית בראשית הצירים של המישור. זווית הגידול של הספירלה המתאימה נקבעת על ידי הזווית בין הקו לישר המדומה (כלומר נקבעת לפי היחס הקבוע בין החלק המדומה לחלק הממשי של נקודות על הישר).

הפונקציה $x\mapsto x^{k}$ כאשר הקבוע $k$ הוא מספר מרוכב עם חלק מדומה שונה מאפס, ממפה את הישר הממשי לספירלה לוגריתמית במישור המרוכב.

ספירלת הזהב היא ספירלה לוגריתמית שגדלה החוצה בפקטור גידול ששווה ליחס הזהב בעברו כל סיבוב של 90 מעלות (זווית גידול של בערך 17.03239 מעלות). ניתן לקרב אותה על ידי "ספירלת פיבונאצ'י", שמורכבת מסדרה של רבעי מעגלים עם רדיוסים היחסיים למספרי פיבונאצ'י.

ספירלות לוגריתמיות בטבע

פרק זה לוקה בחסר. אנא תרמו למכלול והשלימו אותו.

לזרועות של גלקסיות ספירליות יש לעיתים קרובות צורה של ספירלה לוגריתמית. הגלקסיה בתמונה היא גלקסיית המערבולת.

במספר תופעות טבעיות ניתן למצוא עקומים שקרובים ללהיות ספירלות לוגריתמיות. כאן מובאות מספר דוגמאות והסיבות לכך:

• המעוף של הנץ אל הטרף שלו מהווה דוגמה לספירלה לוגריתמית המתכנסת פנימה. כיוון שהנץ רואה גופים בצורה החדה ביותר בזווית העין שלו, כשהוא עף אל הטרף שלו הוא תמיד שומר על זווית קבועה בין כיוון מעופו וקו הראייה שלו אל הטרף, וזווית זאת היא למעשה זווית הקיטון (או הגידול) של הספירלה.
• הזרועות של גלקסיות ספירליות. לגלקסיה שלנו, שביל החלב, יש מספר זרועות ספירליות, ואחת מהן היא בקירוב ספירלה לוגריתמית עם זווית גידול של 12 מעלות.
• העצבים של הקרנית בעין.
• לסופות טרופיות רבות, כגון הוריקנים, יש תבנית של ספירלה לוגריתמית.
• במבנים ביולוגיים רבים כולל הקליפות של רכיכות.

ראו גם

• ספירלת ארכימדס

קישורים חיצוניים

מדיה וקבצים בנושא ספירלה לוגריתמית בוויקישיתוף

• ספירלה לוגריתמית, באתר MathWorld (באנגלית)

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

34813099ספירלה לוגריתמית