סלילונית (חשמל)

איור של סלילונית

קווי שדה של שדה מגנטי שנוצר על ידי סלילונית בעלת שבע לולאות (במישור בו נמצא ציר הסלילונית)

סלילונית (קרויה לעיתים סילונית, או בשמה הלועזי סולנואיד) היא סוג של אלקטרומגנט, הנוצר על ידי סליל של תיל מוליך שבו מימד האורך גדול משמעותית מהקוטר. השדה המגנטי הנוצר בתוך סלילונית כאשר מועבר דרכה זרם חשמלי הוא אחיד בגודלו ובכיוונו (בהזנחת תופעות קצה). השם סלילונית הוא תרגום של המונח solénoïde שנטבע בשנת 1823 על ידי אנדרה-מארי אמפר ומקורו יווני.

סלילונית יכולה להיות ישרה, או כפופה כך שציר מרכז הסליל אינו קו ישר. כל עוד אורך הסליל גדול משמעותית מקוטרו, השדה המגנטי יהיה מקביל לציר הסליל בכל נקודה. לדוגמה, האלקטרומגנט הראשון שהדגים ויליאם סטרג'ן בשנת 1824 היה מורכב מסלילונית בצורת פרסה.

ניתוח פיזיקלי

סלילונית רציפה אינסופית

איור 1: סלילונית אינסופית עם שלוש לולאות שרירותיות המסומנות a‏, b, ו-c. האינטגרל של השדה המגנטי על הלולאה c (שלא עובר דרכה זרם חשמלי) הוא אפס, כך שהשדה המגנטי בתוך הסלילונית חייב להיות אחיד על פני רדיוס הגליל.

לצורך נוחות הניתוח נניח שלסלילונית יש אורך אינסופי אך קוטר סופי. "רציפה" פירושו שהסלילונית אינה בנוחה מחוטים נפרדים ברוחב סופי, אלא מחוטים דקים עד אינסוף ללא רווח ביניהם; בהפשטה זו, ניתן לחשוב על הסלילונית כעל יריעה גלילית של חומר מוליך, שהזרם בו הוא רק בכיוון המשיקי (מסביב לגליל, מסומן ב-i), ואין זרם בכיוון האורכי המסומן ב-z.

השדה המגנטי בתוך סלילונית אינסופית הוא אחיד, וחוזקו אינו תלוי במרחק מהציר או בשטח החתך של הסלילונית.

תוצאה זו מתקבלת מניתוח צפיפות השטף המגנטי סביב הסלילונית. באיור 1, ניתן לראות כי קווי השדה מצביעים בכיוון z החיובי בתוך הסלילונית, ובכיוון z השלילי מחוץ לה. זאת לפי כלל יד ימין עבור השדה סביב מוליך. אם נכרוך את יד ימין סביב החץ המסמן את כיוון הזרם (i) כשהאגודל מצביע לכיוון הזרם, קצות האצבעות יצביעו כלפי מעלה כאשר הן בתוך הסליל, וכלפי מטה כאשר הן מחוץ לסליל. משיקולי סימטריה, רכיבי השדה המגנטי שאינן בכיוון z מתאפסים.

נבדוק את הלולאה c הנמצאת כולה בתוך הסלילונית. לפי חוק אמפר, אנו יודעים כי האינטגרל הקווי הסגור של B (וקטור צפיפות השטף המגנטי) על לולאה זו הוא אפס, כיוון שהלולאה אינה מקיפה אף מוליך ולכן הזרם העובר דרכה הוא אפס. הראינו לעיל שהשדה פונה כלפי מעלה בתוך הסלילונית, כך שהאינטגרלים על הקטעים האופקיים של הלולאה c הם אפס. לפיכך האינטגרל על הקטע השמאלי 1 חייב להיות שווה לאינטגרל על הקטע הימני 2. כיוון שתוצאה זו נכונה בלי קשר למיקום הלולאה ולאורכה, האינטגרנדים (השדות המגנטיים על שני הקטעים) חייבים להיות שווים, ומכאן שהשדה המגנטי בתוך הסלילונית האינסופית הוא אחיד רדיאלית.

ניתן ליישם טיעון דומה על הלולאה a כדי להסיק שהשדה מחוץ לסלילונית הוא אחיד וקבוע רדיאלית. מכך אפשר להסיק שצפיפות השטף מחוץ לסלילונית האינסופית היא אפסית. ניתן להסביר זאת אינטואיטיבית בכך שקווי שדה מגנטי הם תמיד לולאות סגורות (ראה חוק גאוס למגנטיות). בתוך הסלילונית לקווי השדה המגנטי יש צפיפות סופית, אך כל קו נסגר ללולאה (במרחק אינסופי). מאחר שבכל מישור ניצב לציר z, השטח שבתוך הסלילונית הוא סופי בעוד שהשטח מחוץ לה הוא אינסופי, וגודל השדה בחוץ קבוע, הרי שצפיפות קווי השדה מחוץ לסלילונית קטנה "פי אינסוף" מצפיפותם בתוכה, ולכן השדה בחוץ חייב להיות אפסי.

קטע סופי של סלילונית אינסופית

התמונה מראה כיצד ניתן להחיל את חוק אמפר על קטע של סלילונית

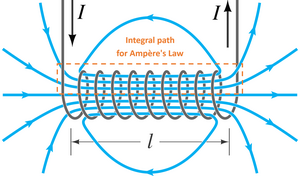
החלת חוק אמפר על מסלול סופי בתוך סלילונית (ראו איור מימין) תיתן את המשוואה לקטע סופי של סלילונית:

$Bl=\mu _{0}NI$

כאשר $B$ היא צפיפות השטף המגנטי, $l$ הוא אורך קטע הסלילונית, $\mu _{0}$ היא פרמאביליות הריק, $N$ הוא מספר הכריכות בקטע, ו-$I$ הוא הזרם הזורם בסלילונית. מכאן נקבל את הנוסחה לצפיפות השטף המגנטי בסלילונית:

$B=\mu _{0}{\frac {NI}{l}}$

משוואה זו תקפה עבור סלילונית בחלל ריק. אם הסלילונית נמצאת בתווך עם פרמאביליות יחסית $\mu _{\mathrm {r} }$, אז השדה גדל באותו יחס:

$B=\mu _{0}\mu _{\mathrm {r} }{\frac {NI}{l}}$

הכללת ליבה מחומר פרומגנטי, כגון ברזל, בתוך פנים הסלילונית, תגביר את צפיפות השטף המגנטי בתוך הסלילונית, אך לא מחוץ לה. כתוצאה מכך, צפיפות השטף בתוך הסלילונית תלויה הן בחומר הליבה והן בגאומטריה שלה, דבר הבא לידי ביטוי בנוסחה

$B=\mu _{0}\mu _{\mathrm {eff} }{\frac {NI}{l}}=\mu {\frac {NI}{l}}$

כאשר $\mu _{\mathrm {eff} }$ היא הפרמאביליות האפקטיבית של הליבה, שהיא פונקציה של התכונות הגאומטריות של הליבה ושל הפרמאביליות היחסית שלה. הפרמאביליות היחסית (תכונה של החומר בלבד) והפרמאביליות האפקטיבית (תכונה של המבנה כולו) יכולות להיות שונות בסדרי גודל רבים.

עבור מבנה מגנטי פתוח, הקשר בין הפרמאביליות האפקטיבית והיחסית ניתן בנוסחה הבאה:

$\mu _{\mathrm {eff} }={\frac {\mu _{r}}{1+k(\mu _{r}-1)}}$

כאשר k הוא גורם הדה-מגנטיזציה של הליבה.

סלילונית רציפה סופית

קווי שדה מגנטי וצפיפות שנוצרו על ידי סלילונית עם צפיפות זרם קבועה

ניתן לנתח סלילונית בעלת אורך סופי, אך רציפה במובן שהזרם אינו זורם בחוטים נפרדים אלא על חוטים דקים וצפופים עד אינסוף, היוצרים יריעת חומר מוליך. אנו מניחים שהזרם מפולג באופן אחיד על פני הסלילונית, עם צפיפות זרם K; בקואורדינטות גליליות:

${\vec {K}}={\frac {I}{l}}{\hat {\phi }}$

ניתן למצוא את השדה המגנטי באמצעות הפוטנציאל המגנטי הווקטורי, אשר עבור סלילונית סופית עם רדיוס R ואורך l בקואורדינטות גליליות $(\rho ,\phi ,z)$ הוא

$A_{\phi }={\frac {\mu _{0}I}{2\pi }}{\frac {1}{l}}{\sqrt {\frac {R}{\rho }}}\left[\zeta k\left({\frac {k^{2}+h^{2}-h^{2}k^{2}}{h^{2}k^{2}}}K(k^{2})-{\frac {1}{k^{2}}}E(k^{2})+{\frac {h^{2}-1}{h^{2}}}\Pi (h^{2},k^{2})\right)\right]_{\zeta _{-}}^{\zeta _{+}}$

כאשר:

• $\zeta _{\pm }=z\pm {\frac {l}{2}}$
• $h^{2}={\frac {4R\rho }{(R+\rho )^{2}}}$
• $k^{2}={\frac {4R\rho }{(R+\rho )^{2}+\zeta ^{2}}}$
• $K(m)=\int _{0}^{\frac {\pi }{2}}{\frac {d\theta }{\sqrt {1-m\sin ^{2}\theta }}}$
• $E(m)=\int _{0}^{\frac {\pi }{2}}{\sqrt {1-m\sin ^{2}\theta }}\,d\theta$
• $\Pi (n,m)=\int _{0}^{\frac {\pi }{2}}{\frac {d\theta }{(1-n\sin ^{2}\theta ){\sqrt {1-m\sin ^{2}\theta }}}}$

כאן, $K(m)$, $E(m)$, ו-$\Pi (n,m)$ הם אינטגרלים אליפטיים שלמים מהסוג הראשון, השני והשלישי.

באמצעות המשוואה ${\vec {B}}=\nabla \times {\vec {A}}$ מתקבלת המשוואות עבור צפיפות השטף המגנטי:

$B_{\rho }={\frac {\mu _{0}I}{4\pi }}{\frac {2}{l}}{\sqrt {\frac {R}{\rho }}}\left[{\frac {k^{2}-2}{k}}K(k^{2})+{\frac {2}{k}}E(k^{2})\right]_{\zeta _{-}}^{\zeta _{+}}$

$B_{z}={\frac {\mu _{0}I}{4\pi }}{\frac {1}{l}}{\frac {1}{\sqrt {R\rho }}}\left[\zeta k\left(K(k^{2})+{\frac {R-\rho }{R+\rho }}\Pi (h^{2},k^{2})\right)\right]_{\zeta _{-}}^{\zeta _{+}}$

על ציר הסימטריה, הרכיב הרדיאלי נעלם, ומרכיב השדה הצירי הוא

$B_{z}={\frac {\mu _{0}NI}{2}}\left({\frac {l/2-z}{l{\sqrt {R^{2}+(l/2-z)^{2}}}}}+{\frac {l/2+z}{l{\sqrt {R^{2}+(l/2+z)^{2}}}}}\right)$

בתוך הסלילונית, רחוק מהקצוות ($l/2-|z|\gg R$), השדה הוא בקירוב קבוע $B=\mu _{0}NI/l$.

השראות

כפי שמוצג לעיל, צפיפות השטף המגנטי $B$ בתוך הסלילונית היא כמעט קבועה וניתנת על ידי

$B=\mu _{\mathrm {eff} }{\frac {NI}{l}}$

כאשר $\mu _{\mathrm {eff} }$ היא הפרמאביליות, $N$ מספר הסיבובים, $I$ הזרם ו-$l$ אורך הסליל. בהתעלם מהשפעות קצה, השטף המגנטי הכולל דרך הסלילונית מתקבל על ידי הכפלת צפיפות השטף $B$ בשטח החתך $A$ :

$\Phi =\mu _{0}{\frac {NIA}{l}}$

בשילוב עם הגדרת ההשראות, $L={\frac {N\Phi }{I}}$, מתקבלת נוסחת השראות הסלילונית:

$L=\mu _{0}{\frac {N^{2}A}{l}}$

עבור סלילונית עם ליבה מגנטית, ניתוח זה מתאים רק כאשר אורך הסליל גדול בהרבה ממכפלת הפרמאביליות היחסית של הליבה המגנטית והקוטר. תנאי זה מגביל את הניתוח הפשוט לליבות בעלות פרמאביליות נמוכה, או לסלילוניות דקות וארוכות במיוחד.

ראו גם

• שסתום סולנואיד
• סליל הלמהולץ
• סליל השראה
• סולנואיד

קישורים חיצוניים

מדיה וקבצים בנושא סלילונית בוויקישיתוף

• הדגמה אינטראקטיבית: שדה מגנטי של סולנואיד, באתר MagLab (המעבדה הלאומית לשדות מגנטיים גבוהים)
• הסבר ומחשבון לסלילוניות, המחלקה לפיזיקה ואסטרונומיה, אוניברסיטת Georgia State
• סלילונית, באתר אנציקלופדיה בריטניקה (באנגלית)

הערות שוליים

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

38683568סלילונית (חשמל)