כלל יד ימין

קובץ:Rechte-hand-regel.jpg

איור 1 - המחשת הניסוח הראשון של כלל יד ימין - אם מכוונים את האגודל בכיוון הווקטור הראשון במכפלה, הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec a} ואת האצבע המורה בכיוון הווקטור השני במכפלה, ${\vec {b}}$, אזי תוצאת המכפלה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec c = \vec a\times\vec b} , תהיה בכיוון אליו מכוונת האמה.

במתמטיקה ובפיזיקה, כלל יד ימין הוא כלל מנמוני שימושי לקביעת המגמה של וקטורים המעורבים בתנועה סיבובית, בשדה מגנטי ובאופן כללי - וקטורים הנוצרים על ידי מכפלה וקטורית. מערכת צירים תלת ממדית נקראת מערכת ימנית, אם מתקיים, לפי כלל היד הימנית, הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \hat x \times \hat y = \hat z} .

ניסוח הכלל

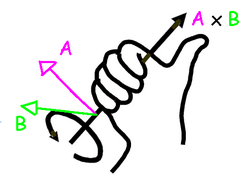
כיוון תוצאת המכפלה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec a \times \vec b} , מוגדר על ידי כלל יד ימין בצורה הבאה: אם האגודל מצביע לכיוון הווקטור הראשון במכפלה, הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec a} , והאצבע המורה מצביעה לכיוון הווקטור השני במכפלה, הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec b} , אז התוצאה, הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec a\times\vec b} , תהיה בכיוון אליו מכוונת האמה (ראו איור 1).

החלפת סדר האצבעות

כל תמורה זוגית, בה הסדר של האצבעות מוחלף באופן מחזורי, גם היא יכולה להיות ניסוח של כלל יד ימין. למשל אם האצבע המורה תצביע לכיוון הווקטור הראשון, והאמה תהיה בכיוון הווקטור השני, האגודל יציע על כיוון התוצאה.

ניסוח נוסף

שגיאה ביצירת תמונה ממוזערת:

איור 2 - תיאור גרפי של הניסוח הנוסף של כלל יד ימין. ניסוח זה מתאים במקרים רבים, למשל: סיבוב כמתואר על ידי אצבעות יד ימין בציור, יתואר על ידי וקטור מהירות זוויתית בכיוון האגודל; זרם חשמלי שזורם בכיוון האגודל יגרום לשדה מגנטי שקוי השדה שלו יהיו טבעות שכיוונן יהיה כיוון האצבעות

בהינתן המכפלה הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec a \times \vec b} , נסובב את הווקטור הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec a} לכיוון הווקטור הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec b} דרך הזווית הקטנה הנוצרת ביניהם. אם נקפל את אצבעות יד ימין כך שכיוון הסיבוב שלהן הוא בכיוון סיבוב זה, האגודל יצביע לכיוון תוצאת המכפלה (ראו איור 2).

מכאן קל לראות ש- הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec a \times \vec b = -\vec b \times \vec a}

שימושים

קובץ:Vector-omega.svg

כיוון המהירות הזוויתית הפענוח נכשל (SVG (אפשר להפעיל MathML בעזרת הרחבת דפדפן): תשובה בלתי־תקינה ("Math extension cannot connect to Restbase.") מהשרת "https://wikimedia.org/api/rest_v1/":): {\displaystyle \ \omega } של גוף הנע בתנועה מעגלית נקבע על ידי כלל היד הימנית. אם מקפלים את אצבעות יד ימין בכיוון הסיבוב, האגודל יצביע בכיוון המהירות (ראו איור עליון)

פרט למכפלה וקטורית, שימוש נפוץ בכלל היד הימנית מתבצע בגדלים הקשורים לסיבוב, כמו מהירות זוויתית, תאוצה זוויתית, ובדרך כלל גם מומנט כוח, ותנע זוויתי. גדלים אלה מיוצגים על ידי וקטורים שכיוונם הוא לאורך ציר הסיבוב. המגמה של וקטורים אלה, כלומר הכיוון על הציר שאליו הם מצביעים, היא שרירותית וחסרת משמעות פיזיקלית (לכן וקטורים אלה מכונים לעיתים פסאודו-וקטורים). עם זאת, חשוב לקבוע פעם אחת בצורה אחידה את הכיוון השרירותי הזה, והמוסכמה בעולם המדעי היא שהוא נקבע בעזרת כלל היד הימנית. כך, למחוגי שעון המסתובבים עם כיוון השעון יש מהירות זוויתית בכיוון הנכנס למישור השעון, ולמחוגים המסתובבים נגד כיוון השעון יש מהירות זוויתית בכיוון היוצא ממישור השעון.

כלל היד הימנית מופיע גם בכל הקשור לשדה מגנטי, שגם הוא למעשה פסאודו-וקטור שלמגמתו אין משמעות פיזיקלית. הוא בא לכדי ביטוי בחוק ביו סבר, ובחוקים אחרים הקשורים לשדה המגנטי.

כלל יד שמאל

קובץ:3D Cartesian Coodinate Handedness.jpg

מערכת ימנית מימין, לצד מערכת שמאלית משמאל

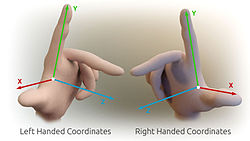
בדומה לכלל יד ימין, ניתן להגדיר גם כלל יד שמאל, ומערכת צירים שמאלית. כרשום קודם, כדי להפחית את הבלבול, משתדלים להתייחס בעיקר למערכת ימנית. אך בשימושים מעשיים, גם למערכת שמאלית יש מקום. למשל, תבריג שמאלי הוא הכרחי במקום שהכוחות הפועלים יגרמו לבורג ימני להשתחרר. דוגמה נוספת היא מנוע חשמלי לעומת מחולל חשמל - גנרטור (generator). בגלל שבשני המקרים יש חילוף תפקידים בין הגורמים לתוצאה, במוסכמות המקובלות, כלל היד השמאלית מתאים למנוע החשמלי. וכלל היד הימנית יתאים למחולל חשמלי.

קישורים חיצוניים

מדיה וקבצים בנושא כלל יד ימין בוויקישיתוף

• ארז גרטי, כללי כף יד בחישוב הכח המגנטי, במדור "מאגר המדע" באתר של מכון דוידסון לחינוך מדעי, 2 ביולי 2011
• כלל יד ימין, באתר MathWorld (באנגלית)

הערך באדיבות ויקיפדיה העברית, קרדיט,
רשימת התורמים
רישיון cc-by-sa 3.0

כלל_יד_ימין20502937Q1366301